一、问题

二、分析

这道题简单的来说就是在图上给定我们起点和终点，从起点到终点会有很多路径，不同的路径会经过不同的点，一条路径上经过的点可以计算出一个和，现在我们需要找出所有的和不同的路线条数。

根据题目中的要求，我们一个点要么向右走，要么向下走，同时根据图中的规律我们会发现，**向右走的数字必定小于向下的数字。**而且必定差1。

这个结论的证明也很简单，如果沿着对角线看的话，我们向右和向下的两个点在对角线上是相邻的，而每个对角线上的点都是从右上角到左下角依次递增的。所以对角线上相邻的两个点必定是差1的，并且右上的大。

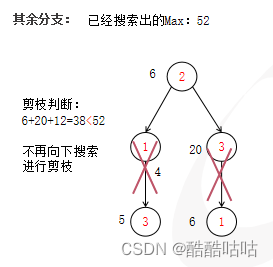
接着我们借用一下题解的图：

由于我们向右走到达的点比我们向下走到达点少1，因此我们就从起点开始一直向右走，走到行的尽头的时候，我们此时只能选择向下走，如下图所示。这种情况下，我们的路径和必定是最小值。

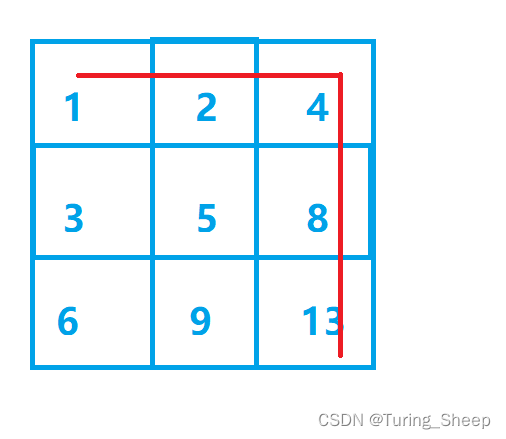
接着我们可以走出最小值加1的路线，我们可以从2到5再到8。

如下图所示：

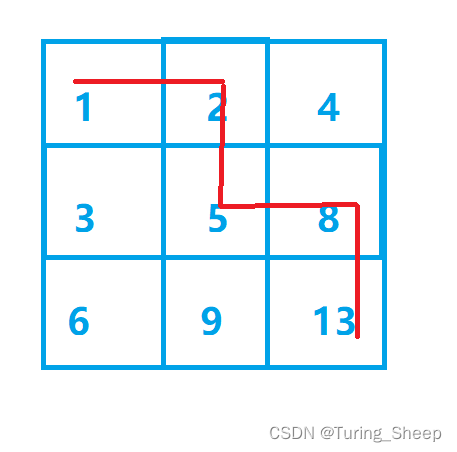
接着，我们还可以走出最小值+2的路线，如下图所示：

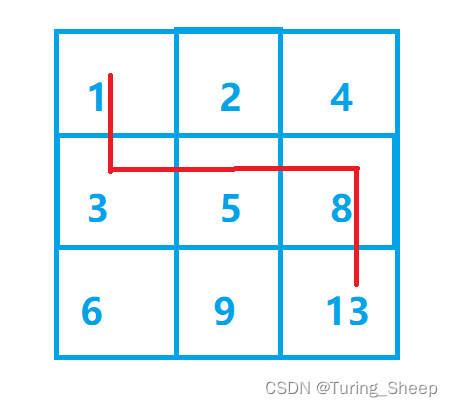
那么能否再继续增大呢？答案是可以的，我们可以从5到9，然后再到13。而后续的过程其实就和上面的过程是一样的了。

我们现在总结一下，再第一行的时候，我们需要做出两次选择。当到该行的最后一次选择的时候，我们已经到了第二行，到了第二行我们依旧可以做2种选择。推广到一般情况：对于任意的起点：$(x_1,y_1)$,终点：$(x_2,y_2)$。我们在每一行可以做：$|x_1-x_2|$此选择，共有$|y_1-y_2|$行允许我们去做选择。所以我们一共能做出$|x_1-x_2|\ast |y_1-y_2|$次选择，而我们还要加上一开始的初始状态。

所以最终的答案就是：$|x_1-x_2|\ast |y_1-y_2|+1$

三、代码

#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 1e5 + 10;

void solve()
{
	int x1, y1, x2, y2;
	cin >> x1 >> y1 >> x2 >> y2;
	cout << (ll)abs(x1 - x2) * abs(y1 - y2) + 1 << endl;	
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin >> t;
	while(t --)
		solve();
}