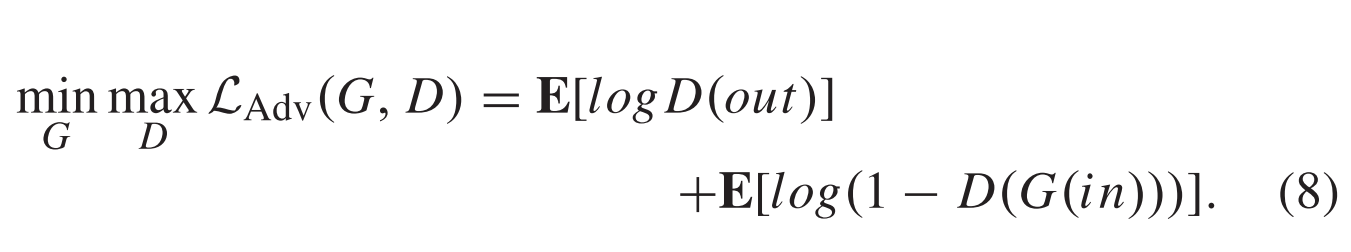1.简单图

简单图：无环无平行边的图。下图：左环右平行边

平凡图：$G=(1,0)$
零图：$G=(p,0)$

2.简单图的补图

补图：对于 $G=(V,E)$，有 E 1 = { u v ∣ u ≠ v 且 u , v ∈ V } E_1=\{uv|u \neq v 且 u,v\in V\} E1​={uv∣u​=v且u,v∈V}，则 $G$ 的补图为：
$$\overline{G}=H=(V,E_1\backslash E)$$ 注意：
1、简单图才有补图；
2、$n$ 阶简单图与其补图的顶点集是相同的；
3、$n$ 阶简单图任意一对顶点邻接(有边)的充要条件是这对顶点在补图中不邻接；
4、$n$ 阶简单图与其补图的边数之和等于完全图 $K_n$ 的边数。

3.图的同构

有 $G=(V,E),H=(U,F)，|V|=|U|$ $$若\exists \phi :V\to U(\phi 是双射)$$ $$且v_1{v}_2\in E\iff \phi (v_1)\phi (v_2)\in F$$ 则称 $G$ 和 $H$ 同构（即给 $V$ 中的顶点重新命名得到新的集合 $U$）。例如下图中，第一行的两个图是相等的，只是画法不同；在第二行，左图选出两个不同颜色的点交换位置，得到右图，则左图和右图为同构。

4.完全图

完全图：是一个简单图，图中任意一个顶点都与其他顶点有且只有一条边连接。$n$ 个顶点的完全图用 $K_n$ 表示，称为 $n$ 阶完全图。例如：

从左往右依次为：1至5阶完全图，即为 $K_1,K_2,K_3,K_4,K_5$ ，完全图的边数为 $\frac{n(n-1)}{2}$。

5.偶图

偶图：在一个图 $G=(V,E)$ 中，顶点集 $V$ 可分解为两个非空子集 $X$ 和 $Y$，且边的两个顶点分别属于 $X$ 和 $Y$ （两个顶点不在同一个子集中）。偶图可以有平行边。如下图：

现实生活中的例子有很多，比如：老师和课程，一个老师可以教多个课程，一个课程可以有多个老师来教。

6.完全偶图

完全偶图：首先是简单偶图（简单图+偶图），其次 $X$ 中的每个顶点都与 $Y$ 中每个顶点相连。 若 $|X|=n$， $|Y|=m$，则完全偶图记为 $K_{n,m}$，边数为 $nm$；如下完全偶图 $K_{3,3}$，顶点分为两部分，蓝色集和红色集，每一个蓝色顶点都与全部红色的顶点邻接，且相同颜色的顶点不邻接。