题目链接

Leetcode.1359 有效的快递序列数目 Rating ： 1723

题目描述

给你 n笔订单，每笔订单都需要快递服务。

请你统计所有有效的 收件/配送 序列的数目，确保第 i 个物品的配送服务 delivery(i)总是在其收件服务 pickup(i)之后。

由于答案可能很大，请返回答案对 10^9 + 7取余的结果。

示例 1：

输入：n = 1
输出：1
解释：只有一种序列 (P1, D1)，物品 1 的配送服务（D1）在物品 1 的收件服务（P1）后。

示例 2：

输入：n = 2
输出：6
解释：所有可能的序列包括：
(P1,P2,D1,D2)，(P1,P2,D2,D1)，(P1,D1,P2,D2)，(P2,P1,D1,D2)，(P2,P1,D2,D1) 和 (P2,D2,P1,D1)。
(P1,D2,P2,D1) 是一个无效的序列，因为物品 2 的收件服务（P2）不应在物品 2 的配送服务（D2）之后。

示例 3：

输入：n = 3
输出：90

提示：

• $1<=n<=500$

分析： 组合数学

对于第 i个服务，有配送服务 Di和 收件服务Pi。题目要求 Di要在 Pi后面，即先收件，再配送。

本题是要求 n个服务所能组成的合法方案。

对于 n个服务的方案，我们讨论能否从 n-1个服务扩展而来。

对于一个共两个服务的合法方案 P1 D1 P2 D2，我们讨论再加上第 3个服务 P3 D3的合法情况。

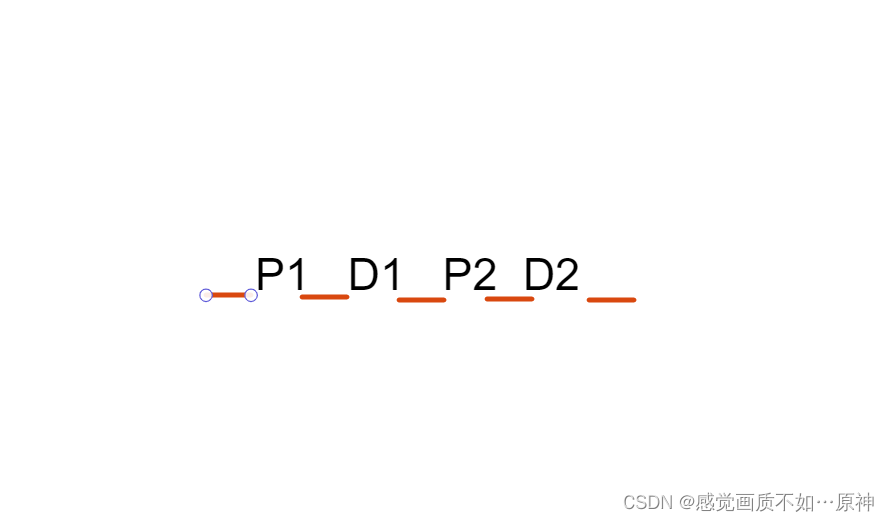
如上图，共 2 * (n - 1) + 1 = 5个位置可以添加。

• 将 P3 D3 当作一个整体插到这 2 * (n - 1) + 1个位置中，即 $C_{2(n-1)+1}^1=5$
• 将 P3 D3分别插入到这 2 * (n - 1) + 1个位置中,即 $C_{2(n-1)+1}^2=10$

两个服务 P1 P2 D1 D2的合法方案有 6个，所以 三个服务 P1 P2 P3 D1 D2 D3的合法方案有 6 * 15 = 90个。

即，$f(n)=f(n-1)\ast (C_{2(n-1)+1}^1+C_{2(n-1)+1}^2)$。

时间复杂度： $O(n)$

C++代码：

using LL = long long;
const int MOD = 1e9 + 7;
class Solution {
public:
    int countOrders(int n) {
        LL ans = 1;
        for(int i = 1;i <= n;i++){
            // 2 * (n - 1) + 1 
            LL a = 2 * (i - 1) + 1;
            
            LL b = a * (a - 1) / 2 + a;
            ans = ans * b % MOD;;
        }
        return ans;
    }
};

Java代码：

class Solution {
    private final int MOD = 1000_000_007;

    public int countOrders(int n) {
        long ans = 1;
        for(int i = 2;i <= n;i++){
            long a = 2 * (i - 1) + 1;
            long b = a * (a - 1)/2 + a;
            ans = ans * b % MOD;
        }
        return (int)ans;
    }
}