来源：力扣（LeetCode）

描述：

如果你熟悉 Shell 编程，那么一定了解过花括号展开，它可以用来生成任意字符串。

花括号展开的表达式可以看作一个由 花括号、逗号 和 小写英文字母 组成的字符串，定义下面几条语法规则：

• 如果只给出单一的元素 x，那么表达式表示的字符串就只有 "x"。R(x) = {x}
  • 例如，表达式 "a" 表示字符串 "a"。
  • 而表达式 "w" 就表示字符串 "w"。
• 当两个或多个表达式并列，以逗号分隔，我们取这些表达式中元素的并集。R({e_1,e_2,...}) = R(e_1) ∪ R(e_2) ∪ ...
  • 例如，表达式 "{a,b,c}" 表示字符串 "a","b","c"。
  • 而表达式 "{{a,b},{b,c}}" 也可以表示字符串 "a","b","c"。
• 要是两个或多个表达式相接，中间没有隔开时，我们从这些表达式中各取一个元素依次连接形成字符串。R(e_1 + e_2) = {a + b for (a, b) in R(e_1) × R(e_2)}
  • 例如，表达式 "{a,b}{c,d}" 表示字符串 "ac","ad","bc","bd"。
• 表达式之间允许嵌套，单一元素与表达式的连接也是允许的。
  • 例如，表达式 "a{b,c,d}" 表示字符串 "ab","ac","ad"​​​​​​。
  • 例如，表达式 "a{b,c}{d,e}f{g,h}" 可以表示字符串 "abdfg", "abdfh", "abefg", "abefh", "acdfg", "acdfh", "acefg", "acefh"。

给出表示基于给定语法规则的表达式 expression，返回它所表示的所有字符串组成的有序列表。

示例 1：

输入：expression = "{a,b}{c,{d,e}}"
输出：["ac","ad","ae","bc","bd","be"]

示例 2：

输入：expression = "{{a,z},a{b,c},{ab,z}}"
输出：["a","ab","ac","z"]
解释：输出中 不应 出现重复的组合结果。

提示：

• 1 <= expression.length <= 60
• expression[i] 由 ‘{’，‘}’，‘,’ 或小写英文字母组成
• 给出的表达式 expression 用以表示一组基于题目描述中语法构造的字符串

方法：递归解析

思路与算法

表达式可以拆分为多个子表达式，以逗号分隔或者直接相接。我们应当先按照逗号分割成多个子表达式进行求解，然后再对所有结果求并集。这样做的原因是求积的优先级高于求并集的优先级。

我们用 expr 表示一个任意一种表达式，用 term 表示一个最外层没有逗号分割的表达式，那么 expr 可以按照如下规则分解：

expr → term ∣ term, expr

其中的 ∣ 表示或者，即 expr 可以分解为前者，也可以分解为后者。

再来看 term, term 可以由小写英文字母或者花括号包括的表达式直接相接组成，我们用 item 来表示每一个相接单元，那么 term 可以按照如下规则分解：

term → item ∣ item term

item 可以进一步分解为小写英文字母 letter 或者花括号包括的表达式，它的分解如下：

item → letter ∣ {expr}

在代码中，我们编写三个函数，分别负责以上三种规则的分解：

1. expr 函数，不断的调用 term，并与其结果进行合并。如果匹配到表达式末尾或者当前字符不是逗号时，则返回。
2. term 函数，不断的调用 item，并与其结果求积。如果匹配到表达式末尾或者当前字符不是小写字母，并且也不是左括号时，则返回。
3. item 函数，根据当前字符是不是左括号来求解。如果是左括号，则调用 expr，返回结果；否则构造一个只包含当前字符的字符串集合，返回结果。

以下示意图以 {a,b}{c,{d,e}} 为例，展示了表达式递归拆解以及回溯的全过程。

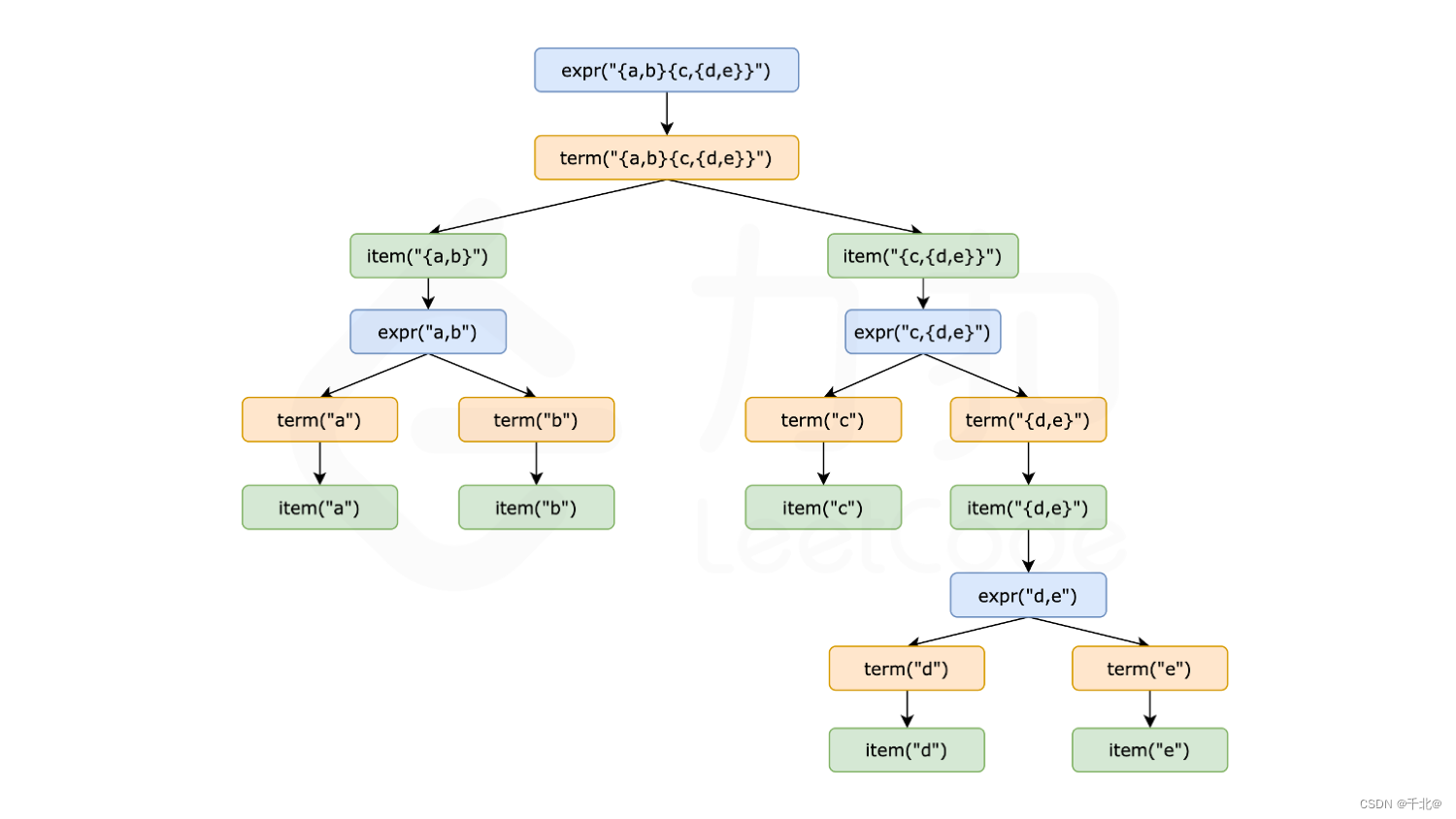
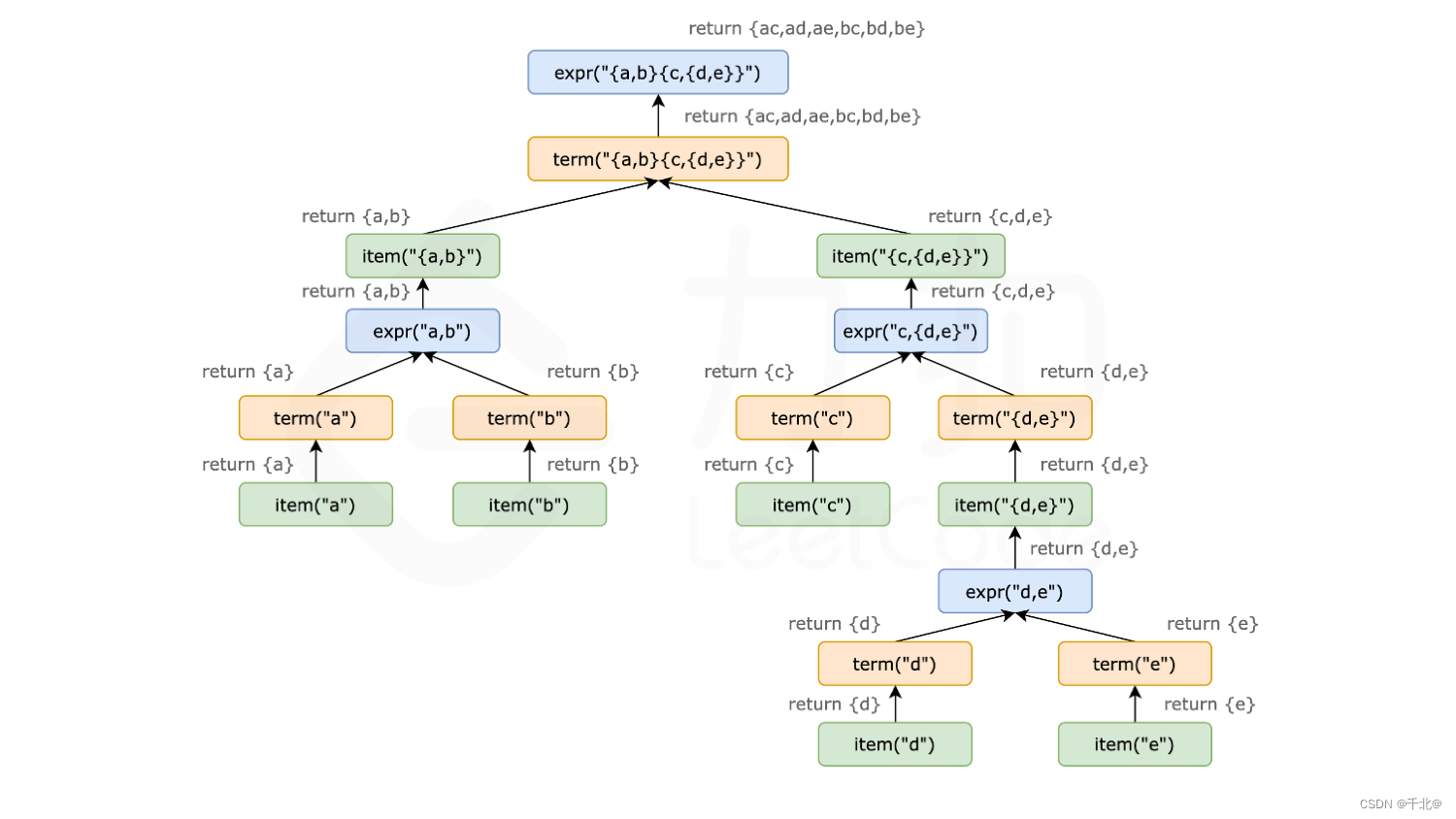
在代码实现过程中有以下细节：

1. 维护一个外部指针来遍历整个表达式，或者将表达式和当前遍历下标以引用的方式传递给被调函数。
2. 因为最终答案需要去重，所以可以先用集合来求解中间结果，最后再转换成已排序的列表作为最终答案。

代码：

class Solution {
    string expression;
    int idx;

    // item -> letter | { expr }
    set<string> item() {
        set<string> ret;
        if (expression[idx] == '{') {
            idx++;
            ret = expr();
        } else {
            ret = {string(1, expression[idx])};
        }
        idx++;
        return move(ret);
    }

    // term -> item | item term
    set<string> term() {
        // 初始化空集合，与之后的求解结果求笛卡尔积
        set<string> ret = {""};
        // item 的开头是 { 或小写字母，只有符合时才继续匹配
        while (idx < expression.size() && (expression[idx] == '{' || isalpha(expression[idx]))) {
            auto sub = item();
            set<string> tmp;
            for (auto &left : ret) {
                for (auto &right : sub) {
                    tmp.insert(left + right);
                }
            }
            ret = move(tmp);
        }
        return move(ret);
    }

    // expr -> term | term, expr
    set<string> expr() {
        set<string> ret;
        while (true) {
            // 与 term() 求解结果求并集
            ret.merge(term());
            // 如果匹配到逗号则继续，否则结束匹配
            if (idx < expression.size() && expression[idx] == ',') {
                idx++;
                continue;
            } else {
                break;
            }
        }
        return move(ret);
    }

public:
    vector<string> braceExpansionII(string expression) {
        this->expression = expression;
        this->idx = 0;
        auto ret = expr();
        return {ret.begin(), ret.end()};
    }
};

执行用时：8 ms, 在所有 C++ 提交中击败了89.66%的用户
内存消耗：10 MB, 在所有 C++ 提交中击败了87.36%的用户
复杂度分析
时间复杂度：O(nlogn)，其中 n 是 expression 的长度。整个
expression 只会遍历一次，时间复杂度为 O(n)，集合合并以及求积运算的时间复杂度为 O(nlogn)，因此总的时间复杂度为 O(nlogn)。
空间复杂度：O(n)。递归过程所需的栈空间为 O(n)，以及存放中间答案的空间复杂度为 O(n)，因此总的空间复杂度为 O(n)。
author：LeetCode-Solution