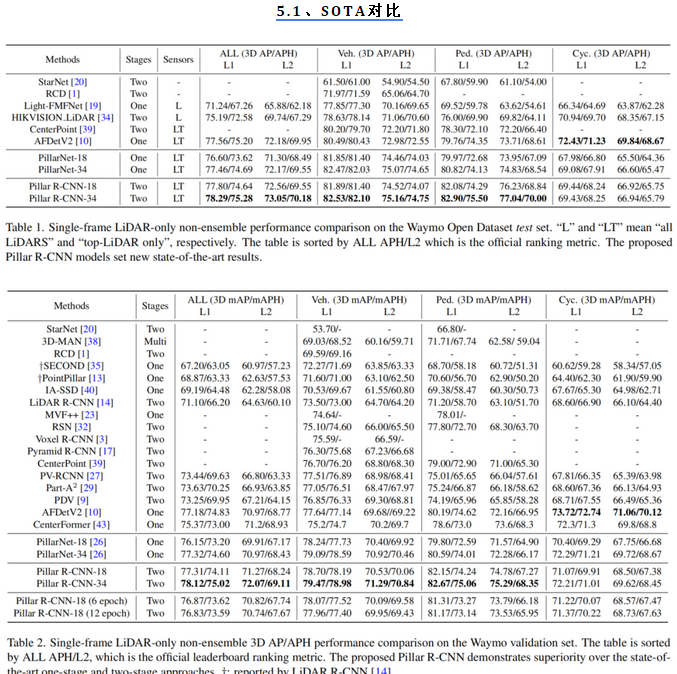
文章目录
- 1、题目一:正方形矩阵顺时针转动90度
- 1.1 题目描述
- 1.2 思路分析
- 1.3 代码实现
- 2、题目二:转圈打印长方形矩阵
- 2.1 题目描述
- 2.2 思路分析
- 2.3 代码实现
- 3、题目三:zigzag打印矩阵
- 3.1 题目描述
- 3.2 思路分析
- 3.3 代码实现
- 4、题目四:输出初始边长为 N 的图案
- 4.1 题目描述
- 4.2 思路分析
- 4.3 代码实现
1、题目一:正方形矩阵顺时针转动90度
1.1 题目描述
给定一个正方形矩阵 matrix,原地 调整成顺时针90度转动的样子

1.2 思路分析
题目解读,就是矩阵根据中心点,每个位置顺时针旋转90度,即如图:
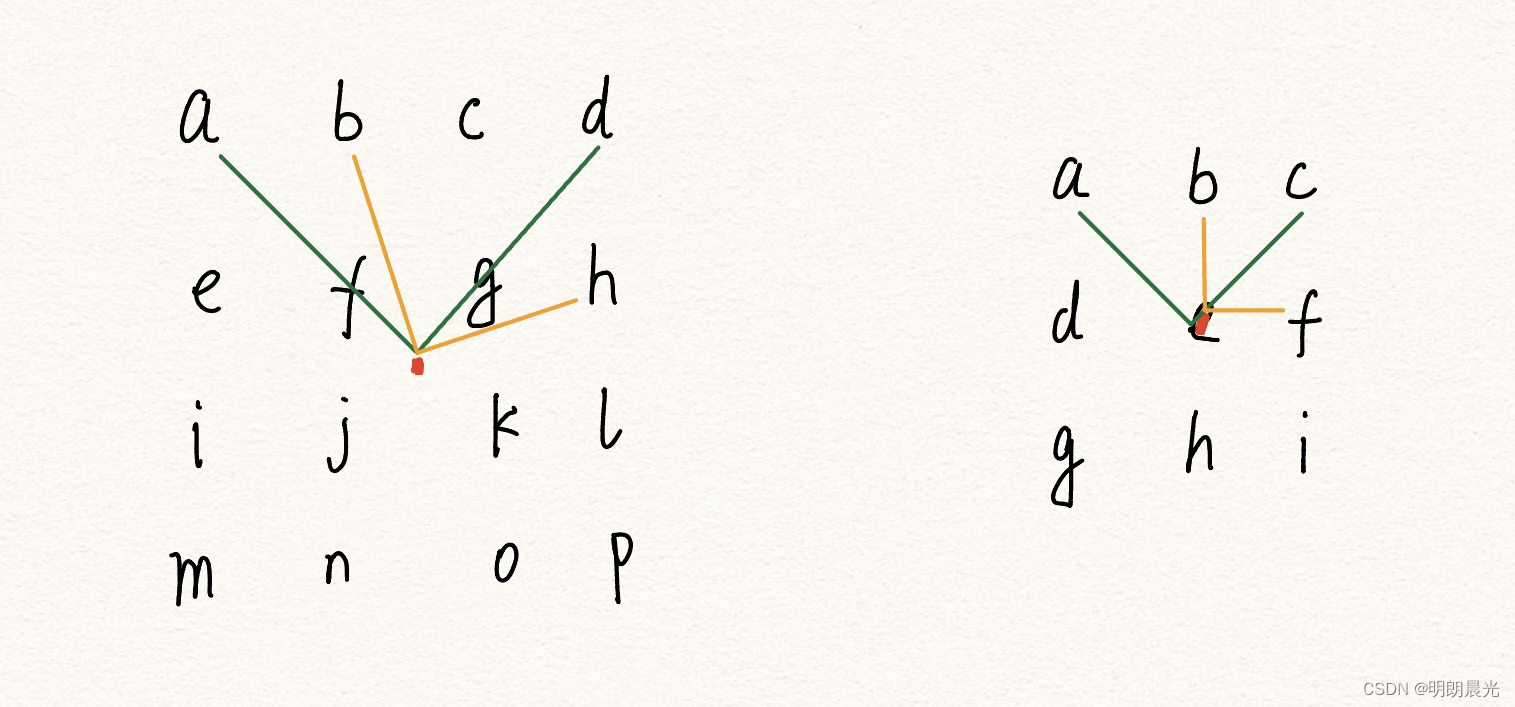
注意,题目要求的是在不申请辅助数组的情况下,原地调整。
题目给定的一定是正方形,因为所使用的内存地址是不会变的。
本题涉及到一个重要的知识点——矩阵的分圈结构。
矩阵的左上角和右下角坐标可以确定矩阵的一圈,而这一圈中的数旋转依然还是在这一圈中。一圈中的数旋转完成后,将左上角和右下角坐标均往里层变化,直到两个坐标发生了错位就表示旋转完成。
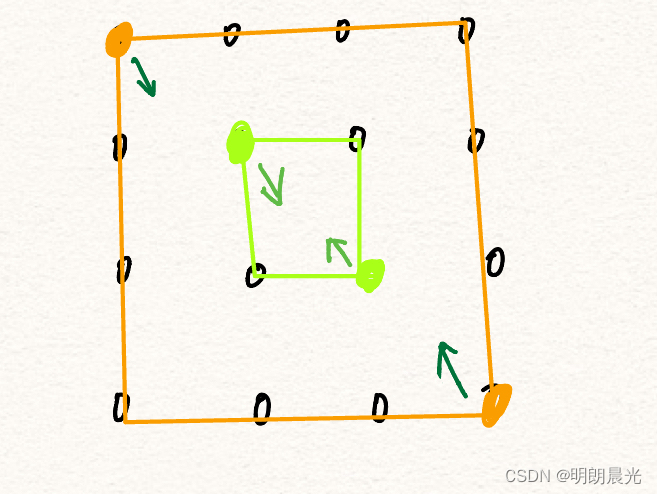
那么一圈中的数怎么调整呢?使用分组。
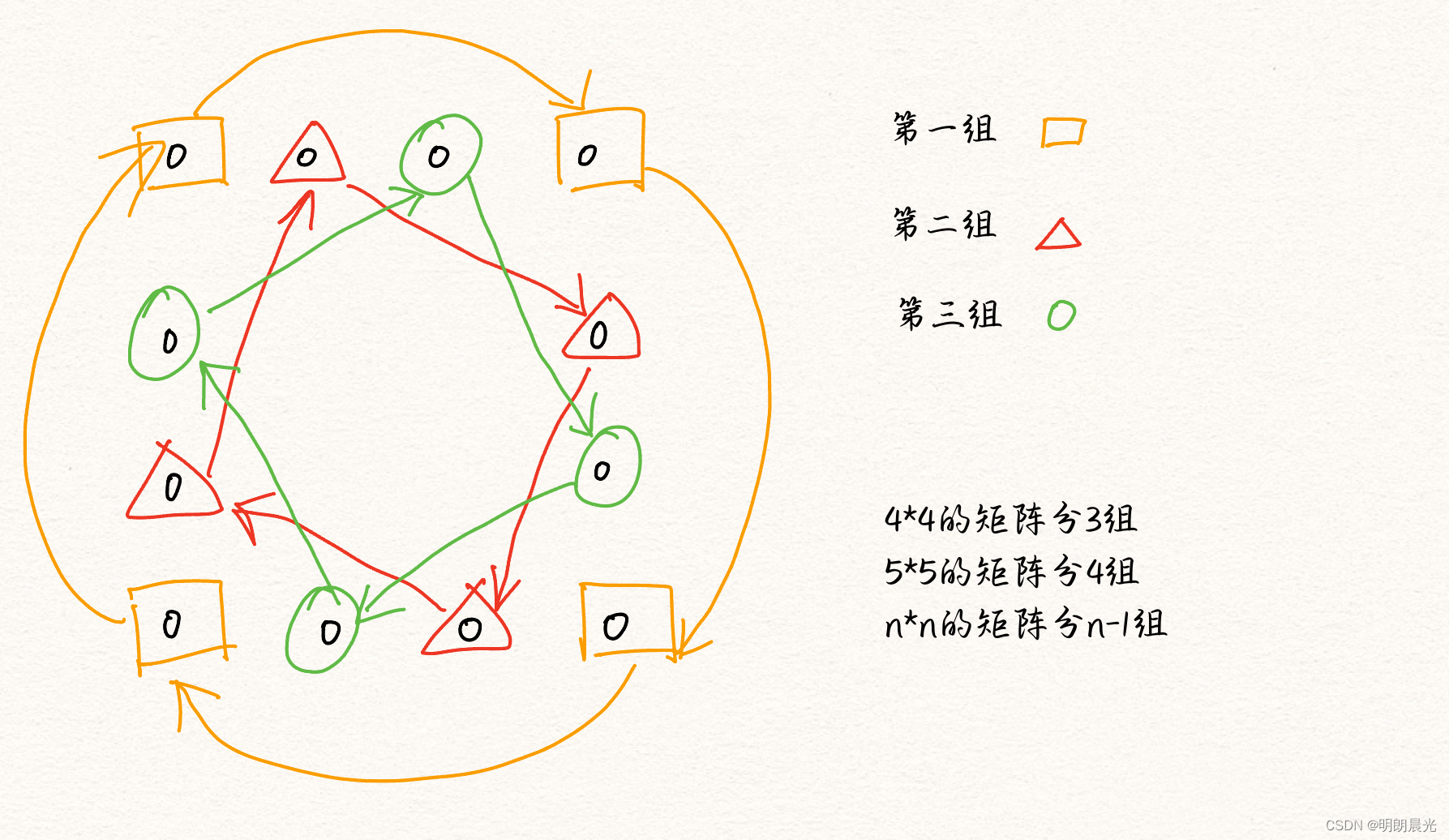
如果整个矩阵的左上角坐标是
(
a
,
b
)
(a, b)
(a,b),右下角坐标是
(
c
,
d
)
(c, d)
(c,d),那么第
i
i
i 组的第一个的坐标是
(
a
,
b
+
i
)
(a, b+i)
(a,b+i),第二个的坐标是
(
a
+
i
,
d
)
(a+i, d)
(a+i,d), 第三个的坐标是
(
c
,
d
−
i
)
(c, d-i)
(c,d−i),第四个坐标是
(
c
−
i
,
b
)
(c-i, b)
(c−i,b)。
启发:矩阵的分圈结构。
1.3 代码实现
public class RotateMatrix {
public static void rotate(int[][] matrix) {
int a = 0;
int b = 0;
int c = matrix.length - 1;
int d = matrix[0].length - 1;
while (a < c) {
rotateEdge(matrix, a++, b++, c--, d--); //圈中调整,调整完成后左上角和右下角坐标往中间变化
}
}
public static void rotateEdge(int[][] m, int a, int b, int c, int d) {
int tmp = 0;
//圈中的每组的四个位置互相变换
for (int i = 0; i < d - b; i++) { //d-b就是组号,表示一共有多少组
tmp = m[a][b + i];
m[a][b + i] = m[c - i][b];
m[c - i][b] = m[c][d - i];
m[c][d - i] = m[a + i][d];
m[a + i][d] = tmp;
}
}
public static void printMatrix(int[][] matrix) {
for (int i = 0; i != matrix.length; i++) {
for (int j = 0; j != matrix[0].length; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 }, { 13, 14, 15, 16 } };
printMatrix(matrix);
rotate(matrix);
System.out.println("=========");
printMatrix(matrix);
}
}
2、题目二:转圈打印长方形矩阵
2.1 题目描述
给定一个长方形矩阵matrix,实现转圈打印
a b c d
e f g h
i j k L
打印顺序:a b c d h L k j i e f g
2.2 思路分析
依然是分圈。
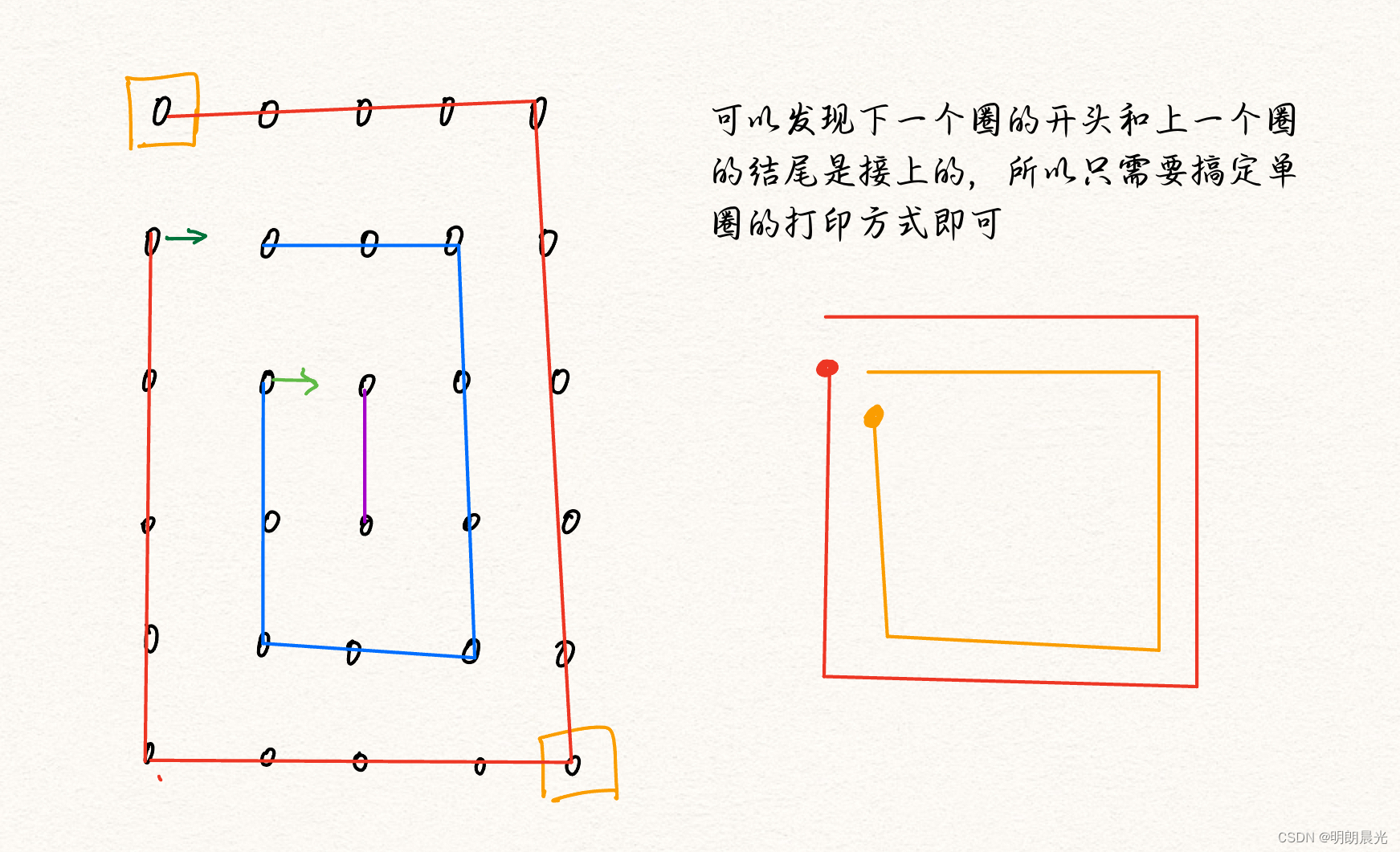
2.3 代码实现
先列举具体的数据量然后再抽象化。
public class PrintMatrixSpiralOrder {
public static void spiralOrderPrint(int[][] matrix) {
int tR = 0;
int tC = 0;
int dR = matrix.length - 1;
int dC = matrix[0].length - 1;
while (tR <= dR && tC <= dC) {
printEdge(matrix, tR++, tC++, dR--, dC--);
}
}
public static void printEdge(int[][] m, int tR, int tC, int dR, int dC) {
if (tR == dR) {
for (int i = tC; i <= dC; i++) {
System.out.print(m[tR][i] + " ");
}
} else if (tC == dC) {
for (int i = tR; i <= dR; i++) {
System.out.print(m[i][tC] + " ");
}
} else {
int curC = tC;
int curR = tR;
while (curC != dC) {
System.out.print(m[tR][curC] + " ");
curC++;
}
while (curR != dR) {
System.out.print(m[curR][dC] + " ");
curR++;
}
while (curC != tC) {
System.out.print(m[dR][curC] + " ");
curC--;
}
while (curR != tR) {
System.out.print(m[curR][tC] + " ");
curR--;
}
}
}
public static void main(String[] args) {
int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
{ 13, 14, 15, 16 } };
spiralOrderPrint(matrix);
}
}
3、题目三:zigzag打印矩阵
3.1 题目描述
给定一个正方形或者长方形矩阵 matrix,实现zigzag打印
0 1 2
3 4 5
6 7 8
打印: 0 1 3 6 4 2 5 7 8
3.2 思路分析
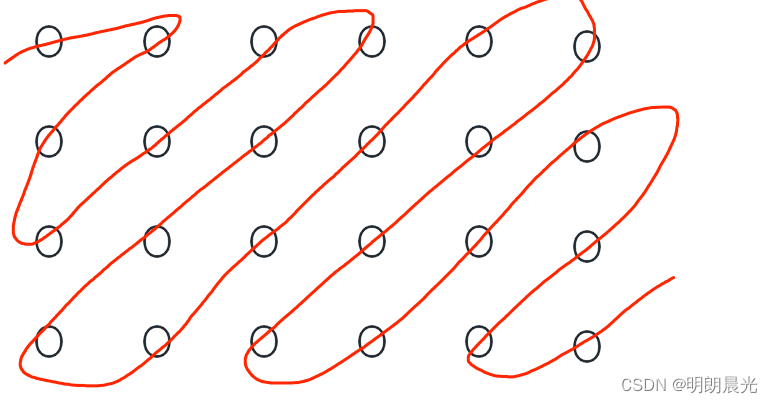
跳出局部,看宏观。
两个点A和B,一开始这两个点都是指的矩阵左上角的点,规定 A 一直往右走,不能再往右的时候往下;而规定B一直往下走,不能再往下的时候往右走。A每走一步,B也要相应地走一步,二者连线是条斜线,将这条斜线打印出来即可。
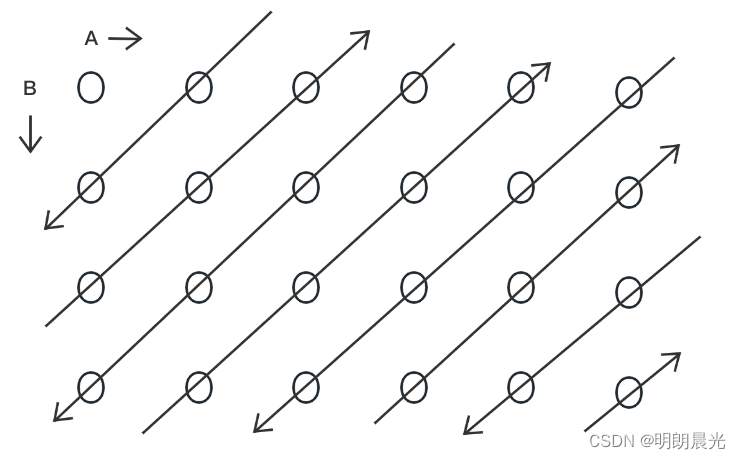
再写一个斜线打印的方程,其中包含从下往上打印和从上向下打印,使用布尔值区分打印方向。
3.3 代码实现
public class ZigZagPrintMatrix {
public static void printMatrixZigZag(int[][] matrix) {
int tR = 0;
int tC = 0;
int dR = 0;
int dC = 0;
int endR = matrix.length - 1;
int endC = matrix[0].length - 1;
boolean fromUp = false;
while (tR != endR + 1) {
printLevel(matrix, tR, tC, dR, dC, fromUp);
tR = tC == endC ? tR + 1 : tR;
tC = tC == endC ? tC : tC + 1;
dC = dR == endR ? dC + 1 : dC;
dR = dR == endR ? dR : dR + 1;
fromUp = !fromUp;
}
System.out.println();
}
//打印斜线
public static void printLevel(int[][] m, int tR, int tC, int dR, int dC, boolean f) {
if (f) {
while (tR != dR + 1) {
System.out.print(m[tR++][tC--] + " "); //从上往下方向
}
} else {
while (dR != tR - 1) {
System.out.print(m[dR--][dC++] + " "); //从下往上方向
}
}
}
public static void main(String[] args) {
int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 } };
printMatrixZigZag(matrix);
}
}
4、题目四:输出初始边长为 N 的图案
4.1 题目描述
给定一个
n
∗
n
n*n
n∗n 的矩阵,在其中按照如下规则填 *。
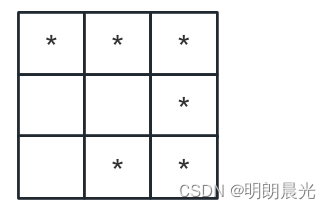
例1:
n
=
3
n=3
n=3
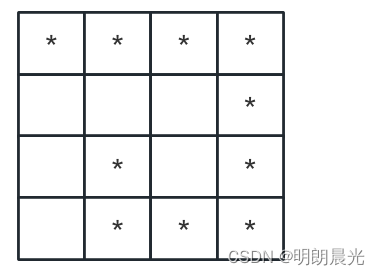
例2:
n
=
4
n=4
n=4
例3:
n
=
5
n=5
n=5
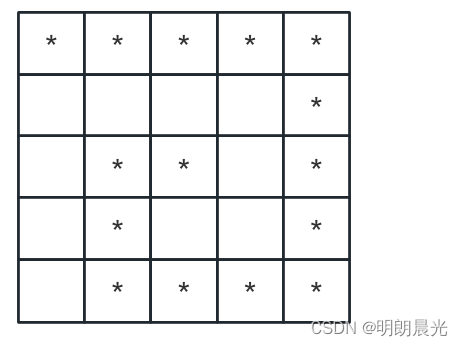
例4:
n
=
10
n=10
n=10
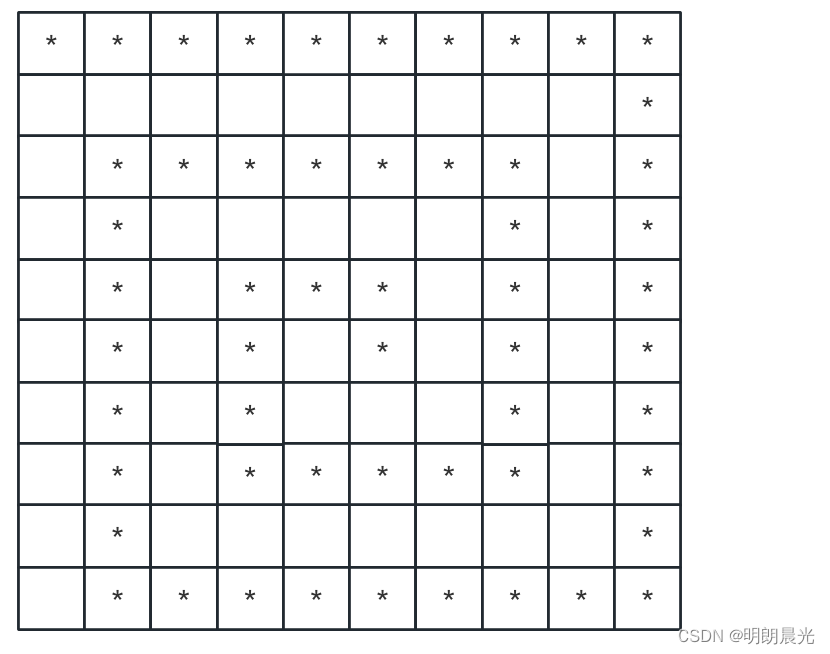
4.2 思路分析
也就是无论往哪个方向填,每个方向都要留个空格避免与之前的 * 碰到。
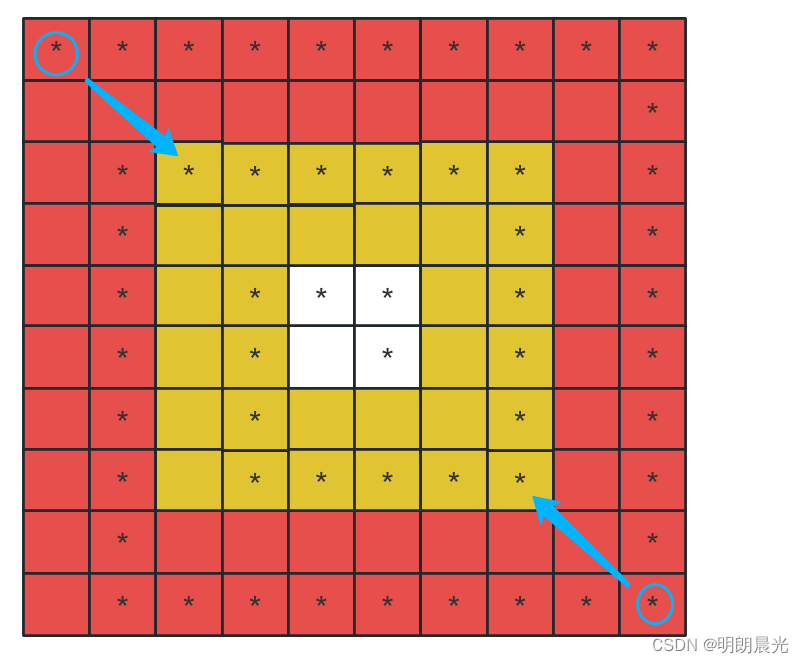
依然是分圈,但是是两层一个圈,当前这个圈打印完后,左上角往右下角跳两层、右下角往左上角跳两层来到第二个圈。搞定每圈的打印,整个图案就可以打印完成。
4.3 代码实现
public class PrintStar {
public static void printStar(int N) {
int leftUp = 0;
int rightDown = N - 1;
char[][] m = new char[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
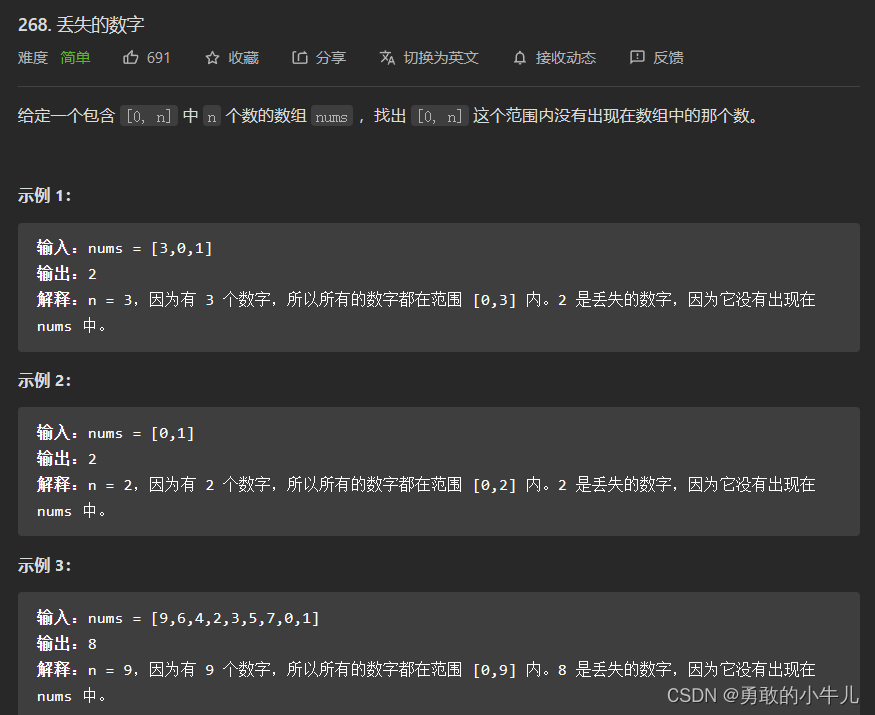
m[i][j] = ' ';
}
}
while (leftUp <= rightDown) {
set(m, leftUp, rightDown);
leftUp += 2;
rightDown -= 2;
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
System.out.print(m[i][j] + " ");
}
System.out.println();
}
}
public static void set(char[][] m, int leftUp, int rightDown) {
for (int col = leftUp; col <= rightDown; col++) {
m[leftUp][col] = '*';
}
for (int row = leftUp + 1; row <= rightDown; row++) {
m[row][rightDown] = '*';
}
for (int col = rightDown - 1; col > leftUp; col--) {
m[rightDown][col] = '*';
}
for (int row = rightDown - 1; row > leftUp + 1; row--) {
m[row][leftUp + 1] = '*';
}
}
public static void main(String[] args) {
printStar(5);
}
}





![[数据结构]:13-插入排序(顺序表指针实现形式)(C语言实现)](https://img-blog.csdnimg.cn/326b864d645e49419a6daeef37135d44.png)