提示:这是力扣上数组类题目里的简单题,按顺序做下来的23道题。
第一题:

关键词:原地修改,有序数组
我的答案: (for循环)
(1)有序数组
class Solution{
public int removeDuplicates(int[] nums){
int k=1;//新数组从第二个元素开始覆盖式加入
for(int i=1;i<nums.length;i++){//从第二个元素开始与前面的元素比较
//因为数组是有序排列,所以只需要判断该元素是否与前一个元素相同即可
if(nums[i]==nums[i-1]){
continue;
}else{//与前面的数组没有相同的元素,覆盖式加入
nums[k++]=nums[i];
}
}
return k;//返回已经删除重复元素的数组长度,只取出原数组的前k位,既得“删除”之意
}
}(2)无序数组
class Solution{
public int removeDuplicates(int[] nums){
int k=1;
for(int i=1;i<nums.length;i++){
//遍历前面的元素,
for(int j=0;j<i;j++){
//若前面已经存在相同的元素,即刻放弃该元素,取下一个元素判断
if(nums[i]==nums[j]){
continue;
}else if(j==i-1){//若已经比较到该元素的前一个元素,都没有相同的,则覆盖式加入原数组
nums[k++]=nums[i];
}
}
}
return k;
}
}
官方答案:(双指针)
class Solution {
public int removeDuplicates(int[] nums) {
int n = nums.length;
//空数组,直接返回
if (n == 0) {
return 0;
}
//快指针用于扫描原数组,慢指针用于存放元素
int fast = 1, slow = 1;
while (fast < n) {
//该元素与前一个元素不相同,则加入
if (nums[fast] != nums[fast - 1]) {
nums[slow] = nums[fast];
++slow;
}
++fast;
}
return slow;//返回新数组长度
}
}第二题:
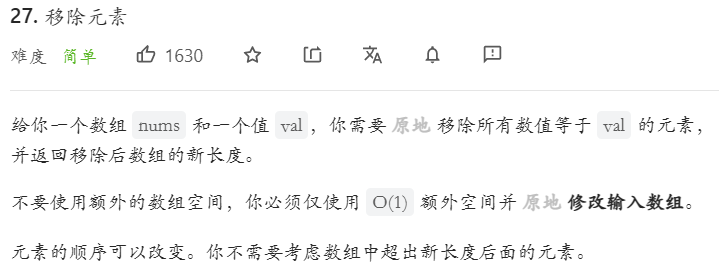
我的答案:
(1)普通解法
class Solution {
public int removeElement(int[] nums, int val) {
int k=0;
//遍历数组的元素
for(int i=0;i<nums.length;i++){
if(nums[i]!=val){//如果不等于val,则覆盖式加入原数组
nums[k++]=nums[i];
}
}
return k;//返回新数组的长度
}
}
代码优化(画手大鹏,for循环挺高级的,有点帅):
class Solution {
public int removeElement(int[] nums, int val) {
int ans = 0;
for(int num: nums) {
if(num != val) {
nums[ans] = num;
ans++;
}
}
return ans;
}
}
(2)双指针(元素都往前移,填补值等于val的元素的空白,元素的顺序不变)
class Solution {
public int removeElement(int[] nums, int val) {
int n=nums.length;
if(n==0){
return 0;//数组为空,直接返回
}
//快指针用于遍历元素,慢指针用于存放筛选后的元素
int fast=0,slow=0;
while(fast<n){//当fast=n时,即为已经遍历了原数组
if(nums[fast]!=val){
nums[slow++]=nums[fast];//存放筛选后的元素
}
fast++;
}
return slow;//返回新数组长度
}
}
官方答案:(双指针,直接取数组最后的元素来填补前面的空白,元素顺序错乱)
class Solution {
public int removeElement(int[] nums, int val) {
int left = 0;//左指针位于数组的头部
int right = nums.length;//右指针位于数组的尾部
while (left < right) {//当left==right时,已经遍历了原数组
if (nums[left] == val) {
nums[left] = nums[right - 1];//如果left值为val,则取(复制)最后一个元素的值来覆盖它,右指针往前移一步。然后重新判断left的值是否等于val,如果还是等于,就再次重复上述步骤
right--;//右指针往前移
} else {
left++;//左指针往后移
}
}
return left;//返回新数组的长度
}
}
第三题
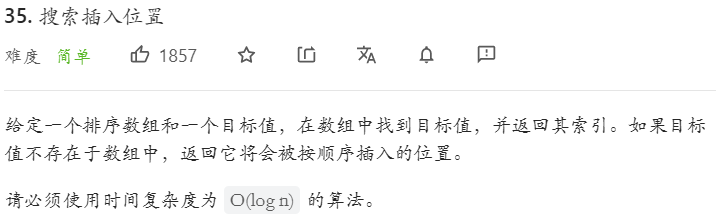
我的答案(逐个查找):
class Solution {
public int searchInsert(int[] nums, int target) {
int n=nums.length;//数组长度
for(int i=0;i<n;i++){
if(nums[i]==target){//找到与目标值相同的元素
return i;//返回元素的位置
}else if(nums[i]>target){//测试数组是升序数组,如果发现比目标值高的就停下(前面的都是比目标值矮的),插队
return i;
}
}
return n;//整个数组都没有比目标值高的元素,所以目标值插在最后的位置,下标值正好等于数组的长度值n
}
}
官方答案(二分查找法):
class Solution {
public int searchInsert(int[] nums, int target) {
int n = nums.length;
int left = 0, right = n - 1, ans = n;//ans 初值设置为数组长度可以省略边界条件的判断,因为存在一种情况是target 大于数组中的所有数,此时需要插入到数组长度的位置。
while (left <= right) {//数组有奇数个元素(中间只有一个元素)就用=,有偶数个元素(中间有两个元素)就用<。从两边往中间逼近,最后一个元素的表达方式
int mid = ((right - left) >> 1) + left;
// >> 1 是二进制的数字向右移一位,即除以2的意思
//mid 表示left和right的中间位置的下标,得到两个等分的部分
if (target <= nums[mid]) {//如果target大于mid,则只需要比较后半部分即可,否则就比较前半部分即可。如果target = nums[mid],则表示找到了目标值的下标,下面用ans返回下标即可
ans = mid;//统一用ans返回
right = mid - 1;//mid已经和target比较过了,所以往旁边挪一步,继续找
} else {
left = mid + 1;
}
}
return ans;//返回中间的位置,最终筛剩的位置
}
} 
网友答案(相较于官方的答案,去掉了ans变量):
class Solution {
public int searchInsert(int[] nums, int target) {
int n = nums.length;
int l=0,r=n-1;
while(l<=r){
int mid=l+(r-l)/2;
if(nums[mid]<target)
l=mid+1;
else r=mid-1;
}
return l;
}
}
第四题
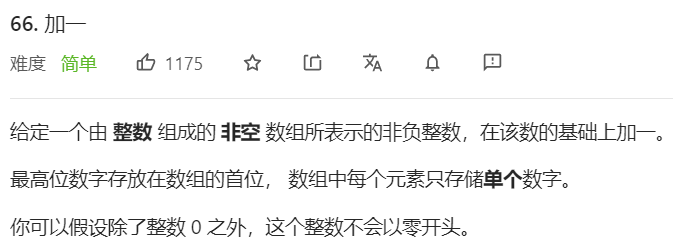
我没写出来
官方答案:
class Solution {
public int[] plusOne(int[] digits) {
int n = digits.length;//数组的长度
for (int i = n - 1; i >= 0; --i) {//从后往前看,逆序遍历
if (digits[i] != 9) {
++digits[i];//第一种情况:digits 最后一位不是9,直接加1
for (int j = i + 1; j < n; ++j) {//前面加1了,把后面的连续几位的9全部置为0(属于第二种情况)
digits[j] = 0;
}
return digits;
}//第二种情况:digits 后面连续几位数字是9,则往前找到第一不是9的数字,加1,后面全部置为0
}
//第三种情况:digits 中所有的元素均为 9
int[] ans = new int[n + 1];//构造一个新数组
ans[0] = 1;//新数组的第一位置为1,后面默认全部为0
return ans;
}
}我困惑的点在于第三种情况,进位后,数组长度超出一位没想到要构建一个新数组。
网友更简洁的答案:
class Solution {
public int[] plusOne(int[] digits) {
for (int i = digits.length - 1; i >= 0; i--) {
digits[i]++;
digits[i] = digits[i] % 10;//如果取余得到0(意味着该位数之前是9),则再往前走一位来加1,
if (digits[i] != 0) return digits;
}
digits = new int[digits.length + 1];
digits[0] = 1;
return digits;
}
}第五题
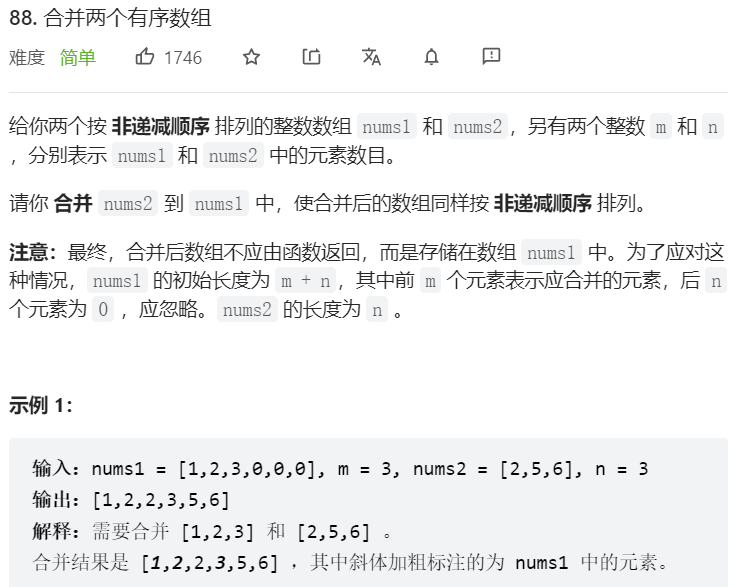
我的答案(运行失败):
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int k=m>n?n:m;//找到最短的数组
for(int i=0;i<k;){
for(int j=0;j<k;){
if(nums1[i]>nums2[j]){
//数组1未比较的元素全部往后移一位,为了插入数组2的元素
j++;
}else if(nums1[i]==nums2[j]){
j++;
i++;
}else if(nums1[i]<nums2[j]){
//不用插入数组2的元素,所以数组1不用挪位,而且继续用该元素
i++;
}
}
}
if(m<n){
for(int i=m;i<m+n;i++){
nums1[i]=nums2[k++];
}
}
}
}
//1、找到最短数组,比较两个数组相同长度的部分,两个指针
//2、比较数组1和数组2最前面的数,分三种情况:>,<,==,移动指针
//4、把最小值排好,然后这次比较的最大值继续与另一个数组的元素进行比较
//5、把较长数组后面多出的部分直接加入到数组1的后面(如果数组1长,则跳过这步)官方答案:
法一:直接合并后排序
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
for (int i = 0; i != n; ++i) {
nums1[m + i] = nums2[i];//把数组2的全部元素放到数组1的后面
}
Arrays.sort(nums1);
}
}
法二:双指针
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int p1 = 0, p2 = 0;//两个指针均指向两个数组的头部
int[] sorted = new int[m + n];//创建一个新数组
int cur;//定义一个中间变量
while (p1 < m || p2 < n) {
if (p1 == m) {//数组1比较短
cur = nums2[p2++];//直接把数组2后面比数组1多出的部分加到排好序的新数组里
} else if (p2 == n) {//数组2比较短
cur = nums1[p1++];//直接把数组1后面比数组2多出的部分加到排好序的新数组里
} else if (nums1[p1] < nums2[p2]) {//元素比较,把较小的加到新数组里
cur = nums1[p1++];
} else {
cur = nums2[p2++];
}
sorted[p1 + p2 - 1] = cur;//把元素插进新数组
}
for (int i = 0; i != m + n; ++i) {//把新数组里合并好的元素全部转移到数组1里
nums1[i] = sorted[i];
}
}
}
法三:逆向双指针
/*nums1的后半部分是空的,可以直接覆盖而不会影响结果。因此可以指针设置为从后向前遍历,每次取两者之中的较大者放进nums1的最后面。*/
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int p1 = m - 1, p2 = n - 1;//两个指针均指向两个数组的尾部
int tail = m + n - 1;
int cur;//临时变量
while (p1 >= 0 || p2 >= 0) {
if (p1 == -1) {//数组1较短
cur = nums2[p2--];//把数组2前面比数组1多出的部分直接加到数组1里
} else if (p2 == -1) {//数组2较短
cur = nums1[p1--];//把数组1前面比数组2多出的部分直接加到数组1里
} else if (nums1[p1] > nums2[p2]) {//元素比较,把较大值插入数组1的后面,从后往前
cur = nums1[p1--];
} else {
cur = nums2[p2--];
}
nums1[tail--] = cur;
}
}
}
//我也是原地修改,但我是从前往后插入,所以面临着数组1前面的元素被覆盖的麻烦第六题
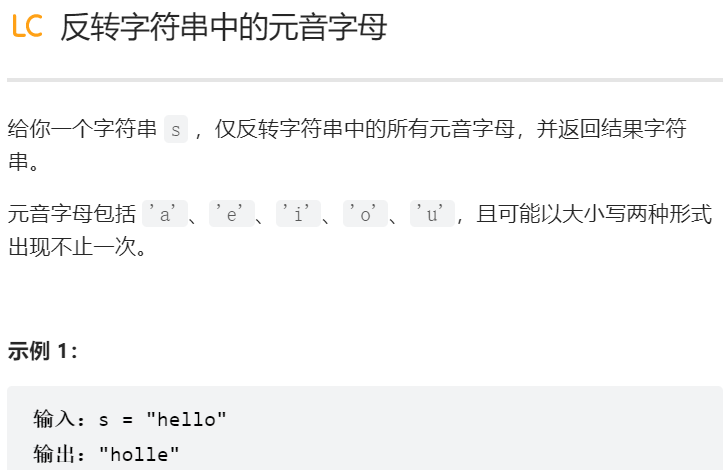
我的答案:
class Solution {//双指针法,对撞指针
public String reverseVowels(String s) {
StringBuffer s1=new StringBuffer(s);//String里的值不能更改,所以转换成StringBuffer类
char t;//定义一个变量,方便后面交换元素
for(int i=0,j=s1.length()-1;i<j;i++){//前指针
if(s1.charAt(i)=='a'||s1.charAt(i)=='i'||s1.charAt(i)=='e'||s1.charAt(i)=='u'||s1.charAt(i)=='o'||s1.charAt(i)=='A'||s1.charAt(i)=='I'||s1.charAt(i)=='E'||s1.charAt(i)=='U'||s1.charAt(i)=='O'){
while(i<j){//后指针
if(s1.charAt(j)=='a'||s1.charAt(j)=='i'||s1.charAt(j)=='e'||s1.charAt(j)=='u'||s1.charAt(j)=='o'||s1.charAt(j)=='A'||s1.charAt(j)=='I'||s1.charAt(j)=='E'||s1.charAt(j)=='U'||s1.charAt(j)=='O'){
//交换前后两个元音字母
t=s1.charAt(i);
s1.replace(i,i+1,String.valueOf(s.charAt(j)));
s1.replace(j,j+1,String.valueOf(t));
j--;
break;
}
j--;
}
}
}
return s1.toString();//把StringBuffer转换回String,返回
}
}
官方答案(双指针):
class Solution {
public String reverseVowels(String s) {
int n = s.length();
char[] arr = s.toCharArray();//把字符串转换成字符数组
int i = 0, j = n - 1;
while (i < j) {
while (i < n && !isVowel(arr[i])) {//不是元音字母就自增,继续找
++i;
}
while (j > 0 && !isVowel(arr[j])) {//不是元音字母就自减,继续找
--j;
}
//两个指针用同等级的前后顺序,或者用内外层循环也可以
if (i < j) {
swap(arr, i, j);
++i;
--j;
}
}
return new String(arr);//把字符数组转换成字符串返回
}
public boolean isVowel(char ch) {//判断是否是元音字母
return "aeiouAEIOU".indexOf(ch) >= 0;//返回字符串"aeiouAEIOU"中字符ch的下标
}
public void swap(char[] arr, int i, int j) {//交换方法
char temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}

第七题

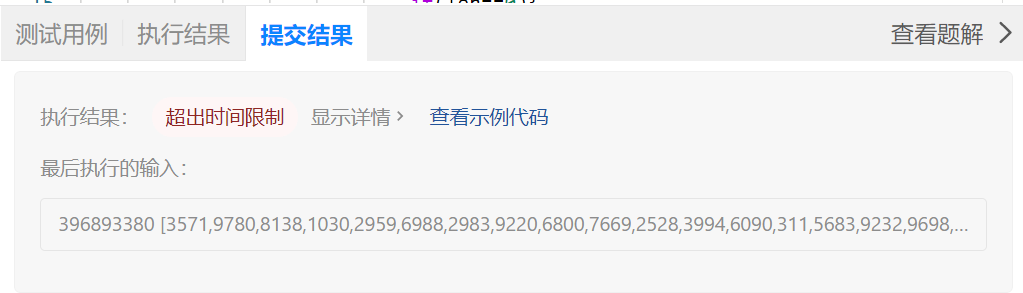
我的答案:
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int sum=0,len=0;
for(int i=0;i<nums.length-1;i++){
if(nums[i]>=target){
return 1;
}else{
sum=nums[i];
for(int j=i+1;j<nums.length;j++){
if(nums[j]>=target){
return 1;
}else{
sum+=nums[j];
if(sum>=target){
if(len==0){
len=j-i+1;
}else{
len=Math.min(len,j-i+1);
break;
}
}
}
}
}
}
return len;
}
}
官方答案:
法一:暴力法
class Solution {
public int minSubArrayLen(int s, int[] nums) {
int n = nums.length;
if (n == 0) {
return 0;
}
int ans = Integer.MAX_VALUE;//找最大值,方便参与下面的取最小值函数
for (int i = 0; i < n; i++) {
int sum = 0;
for (int j = i; j < n; j++) {
sum += nums[j];
if (sum >= s) {
ans = Math.min(ans, j - i + 1);
break;
}
}
}
return ans == Integer.MAX_VALUE ? 0 : ans;//如果ans == Integer.MAX_VALUE,证明没找到符合要求的子数组,返回0
}
}

法二:前缀和+二分查找
class Solution {
public int minSubArrayLen(int s, int[] nums) {
int n = nums.length;
if (n == 0) {
return 0;
}
int ans = Integer.MAX_VALUE;
int[] sums = new int[n + 1];
// 为了方便计算,令 size = n + 1
// sums[0] = 0 意味着前 0 个元素的前缀和为 0
// sums[1] = A[0] 前 1 个元素的前缀和为 A[0]
// 以此类推
for (int i = 1; i <= n; i++) {
sums[i] = sums[i - 1] + nums[i - 1];
}
for (int i = 1; i <= n; i++) {
int target = s + sums[i - 1];
int bound = Arrays.binarySearch(sums, target);
if (bound < 0) {
bound = -bound - 1;
}
if (bound <= n) {
ans = Math.min(ans, bound - (i - 1));
}
}
return ans == Integer.MAX_VALUE ? 0 : ans;
}
}
法二:滑动窗口(降低了时间复杂度)
class Solution {
public int minSubArrayLen(int s, int[] nums) {
int n = nums.length;
if (n == 0) {
return 0;
}
int ans = Integer.MAX_VALUE;
int start = 0, end = 0;//双指针
int sum = 0;
while (end < n) {
sum += nums[end];
while (sum >= s) {
ans = Math.min(ans, end - start + 1);
sum -= nums[start];//减去了最前面的那个,给最后面的那个腾位置,就像用两块砖头走路一样
start++;//指针后移
}
end++;
}
return ans == Integer.MAX_VALUE ? 0 : ans;
}
}