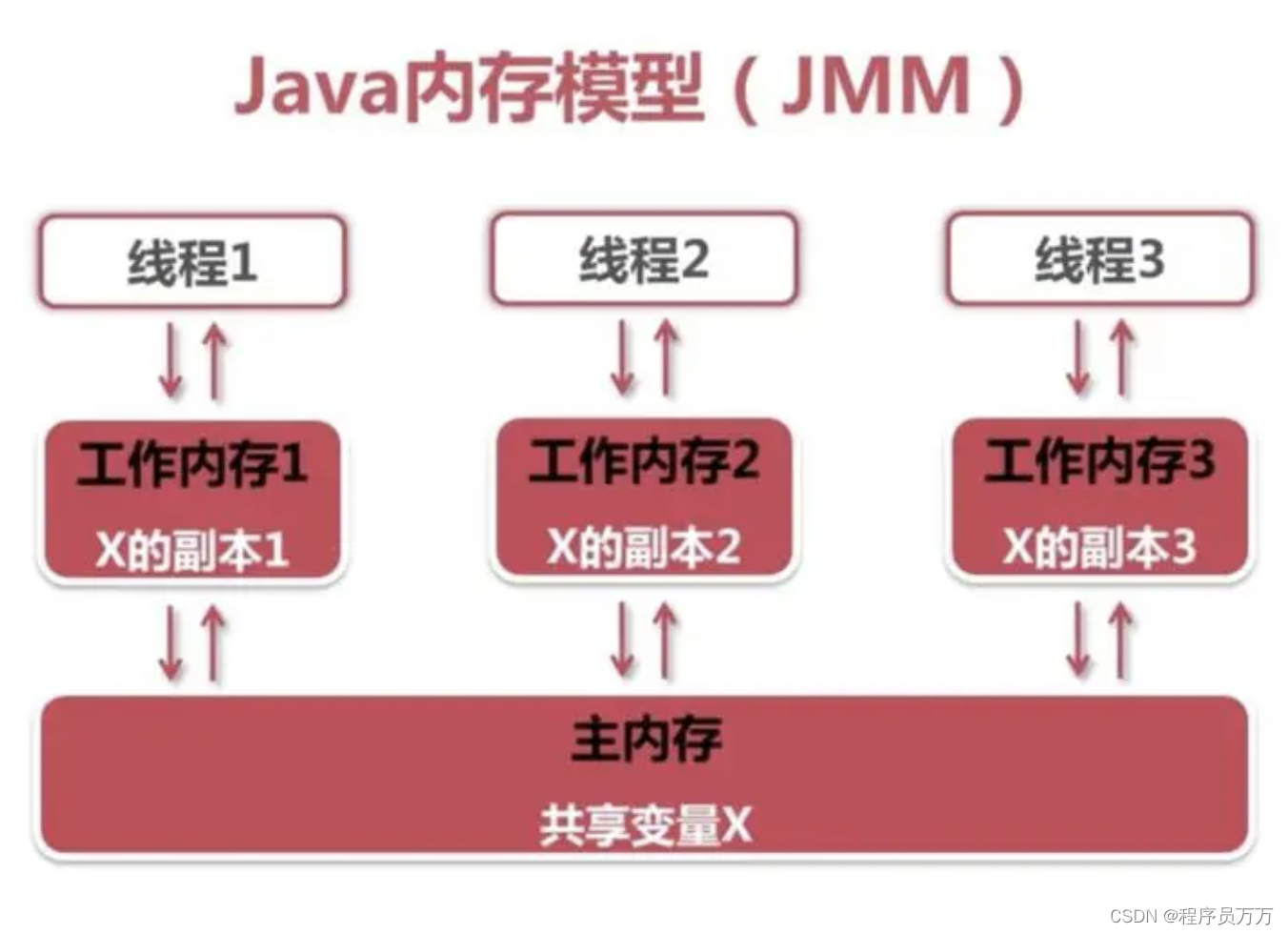
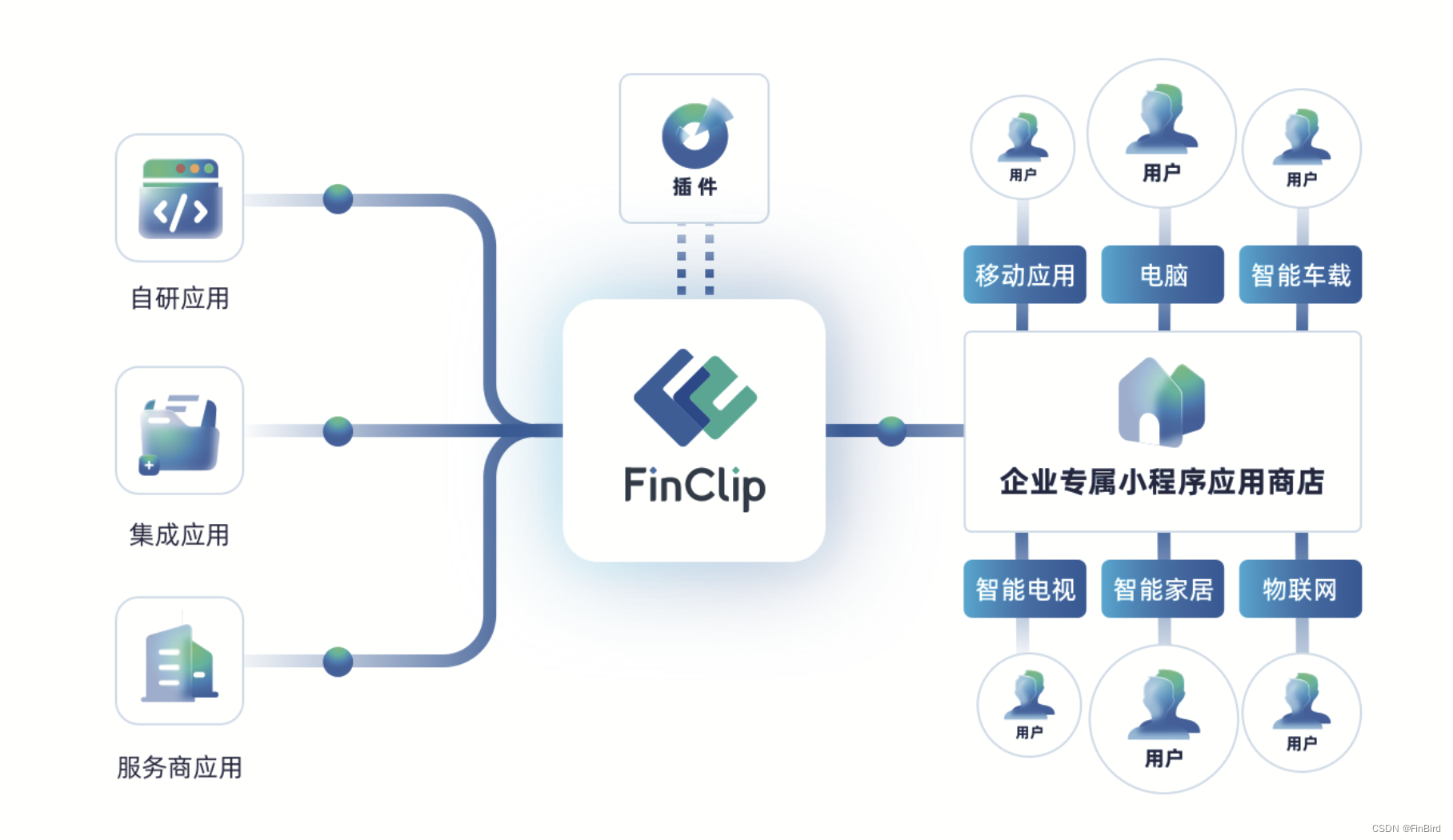
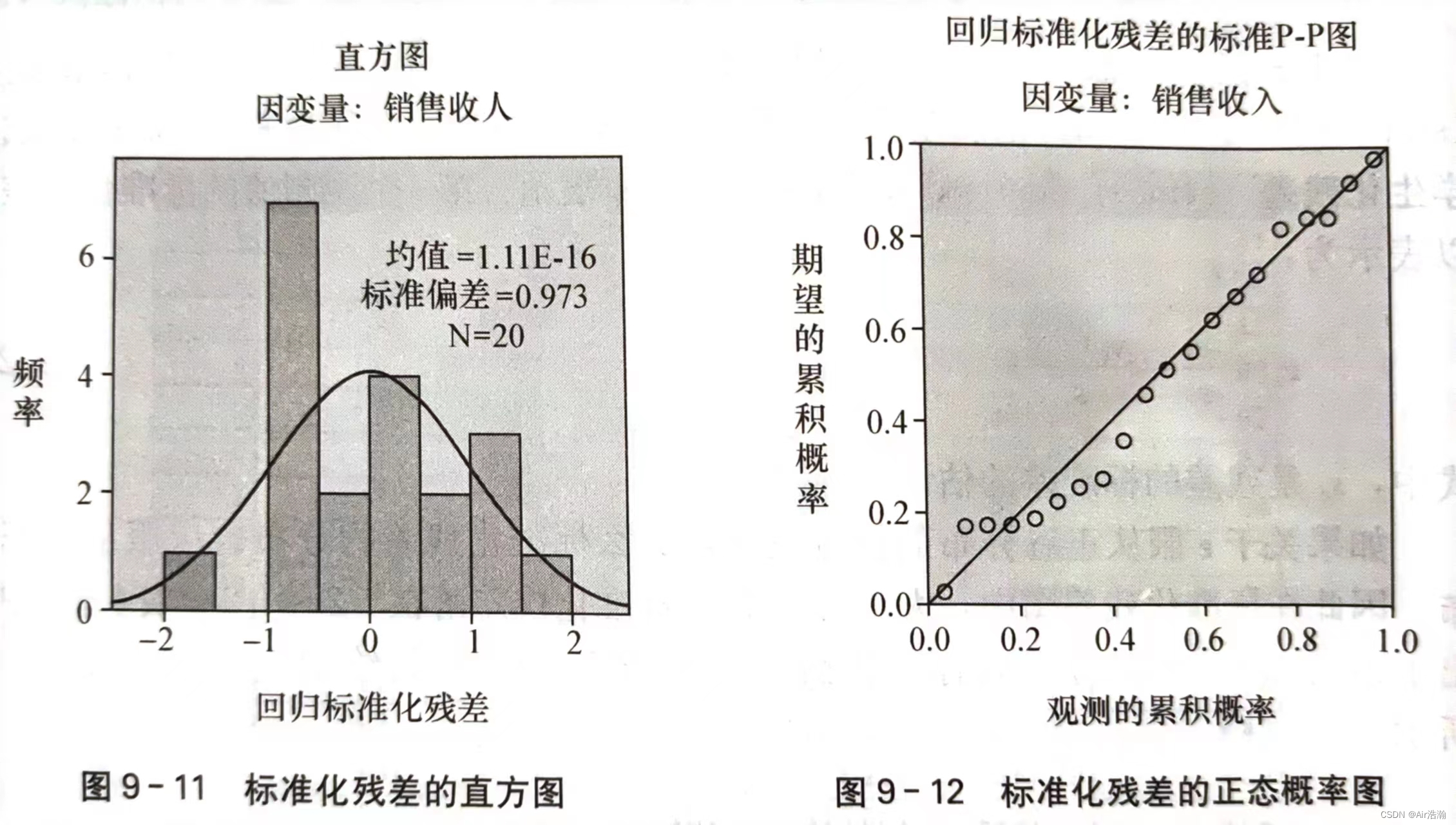
动态规划
- 方格取数
- 垒骰子
方格取数
题目描述
设有 N × N N \times N N×N 的方格图 ( N ≤ 9 ) (N \le 9) (N≤9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 0 0 0。如下图所示(见样例):
A
0 0 0 0 0 0 0 0
0 0 13 0 0 6 0 0
0 0 0 0 7 0 0 0
0 0 0 14 0 0 0 0
0 21 0 0 0 4 0 0
0 0 15 0 0 0 0 0
0 14 0 0 0 0 0 0
0 0 0 0 0 0 0 0
B
某人从图的左上角的
A
A
A 点出发,可以向下行走,也可以向右走,直到到达右下角的
B
B
B 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字
0
0
0)。
此人从
A
A
A 点到
B
B
B 点共走两次,试找出
2
2
2 条这样的路径,使得取得的数之和为最大。
输入格式
输入的第一行为一个整数 N N N(表示 N × N N \times N N×N 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 0 0 0 表示输入结束。
输出格式
只需输出一个整数,表示 2 2 2 条路径上取得的最大的和。
样例 #1
样例输入 #1
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
样例输出 #1
67

注意这里需要分为 i和j 是否相等,如果不相等一定不在同一个格子中,那就可以取两次了,为什么可以优化成三维,是因为如果走的次数是固定的,横坐标和纵坐标的和事固定的(行数+列数)。
注意,有了步数这一实际意义(大于等于0)和 步数与行数之间的约束(后者必须小于前者),循环的嵌套顺序和行数循环终止条件要注意
#include <iostream>
using namespace std;
//#define int long long int
const int N=10;
int a[N][N];
int dp[N][N][N][N];
int n,x,y,s;
int get_max(int u,int v,int o,int p){
return max(max(u,v),max(o,p));
}
signed main(int argc, char** argv) {
cin>>n;
while(cin>>x>>y>>s){
if(!x&&!y&&!s)break;
a[x][y]=s;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
for(int l=1;l<=n;l++){
dp[i][j][k][l]=get_max(dp[i-1][j][k-1][l],dp[i-1][j][k][l-1],dp[i][j-1][k-1][l],dp[i][j-1][k][l-1])+a[i][j]+a[k][l];
// 两个人一步有四种结果
if(i==k&&j==l)dp[i][j][k][l]-=a[i][j];
}
}
}
}
cout<<dp[n][n][n][n];
return 0;
}
#include <iostream>
using namespace std;
//#define int long long int
const int N=10;
int a[N][N];
int dp[N][N][N*2];
int n,x,y,s;
int get_max(int u,int v,int o,int p){
return max(max(u,v),max(o,p));
}
signed main(int argc, char** argv) {
cin>>n;
while(cin>>x>>y>>s){
if(!x&&!y&&!s)break;
a[x][y]=s;
}
dp[1][1][0]=a[1][1];//初始化
for(int k=1;k<=(n-1)*2;k++){//已经走了多少步(两个人是同时走一步)
for(int i=1;i<=min(k+1,n);i++){
for(int j=1;j<=min(k+1,n);j++){
dp[i][j][k]=get_max(dp[i-1][j][k-1],dp[i-1][j-1][k-1],dp[i][j][k-1],dp[i][j-1][k-1])+a[i][k+2-i]+a[j][k+2-j];
// 两个人一步有四种结果 p1向下p2向右,都向下,都向右,p1向右p2向下
if(i==j)dp[i][j][k]-=a[i][k+2-i];
// m行n列总共 m-1+n-1步
// cx行,cx=i,cy列 cx-1+cy-1=k步 cy=k+2-cx
}
}
}
cout<<dp[n][n][(n-1)*2];
return 0;
}
//1 1 1
//2 2 3
//2 3 4
垒骰子

爆搜
#include <iostream>
using namespace std;
#define int long long int
const int mod=1e9+7;
const int N=10;
int m,n,x,y;
int back[7];
bool conflict[40][40];
int dfs(int u,int cnt){
if(cnt==n+1){
return 1;
}
int ans=0;
for(int down=1;down<=6;down++){//枚举骰子底部的数字
if(conflict[u][down])continue;
ans=(ans+dfs(back[down],cnt+1))%mod;
}
}
int quickpow(int b,int e){
b%=mod;
int res=1;
while(e){
if(e&1)res=res*b%mod;
b=b*b%mod;
e=e>>1;
}
return res;
}
signed main(int argc, char** argv) {
back[1]=4;back[4]=1;
back[2]=5;back[5]=2;
back[3]=6;back[6]=3;
cin>>n>>m;
for(int i=0;i<m;i++){
cin>>x>>y;
conflict[x][y]=true;
conflict[y][x]=true;
}
int res=0;
for(int down=1;down<=6;down++){
res=(res+dfs(back[down],2))%mod;
}
res=res*quickpow(4,n)%mod;
cout<<res;
return 0;
}
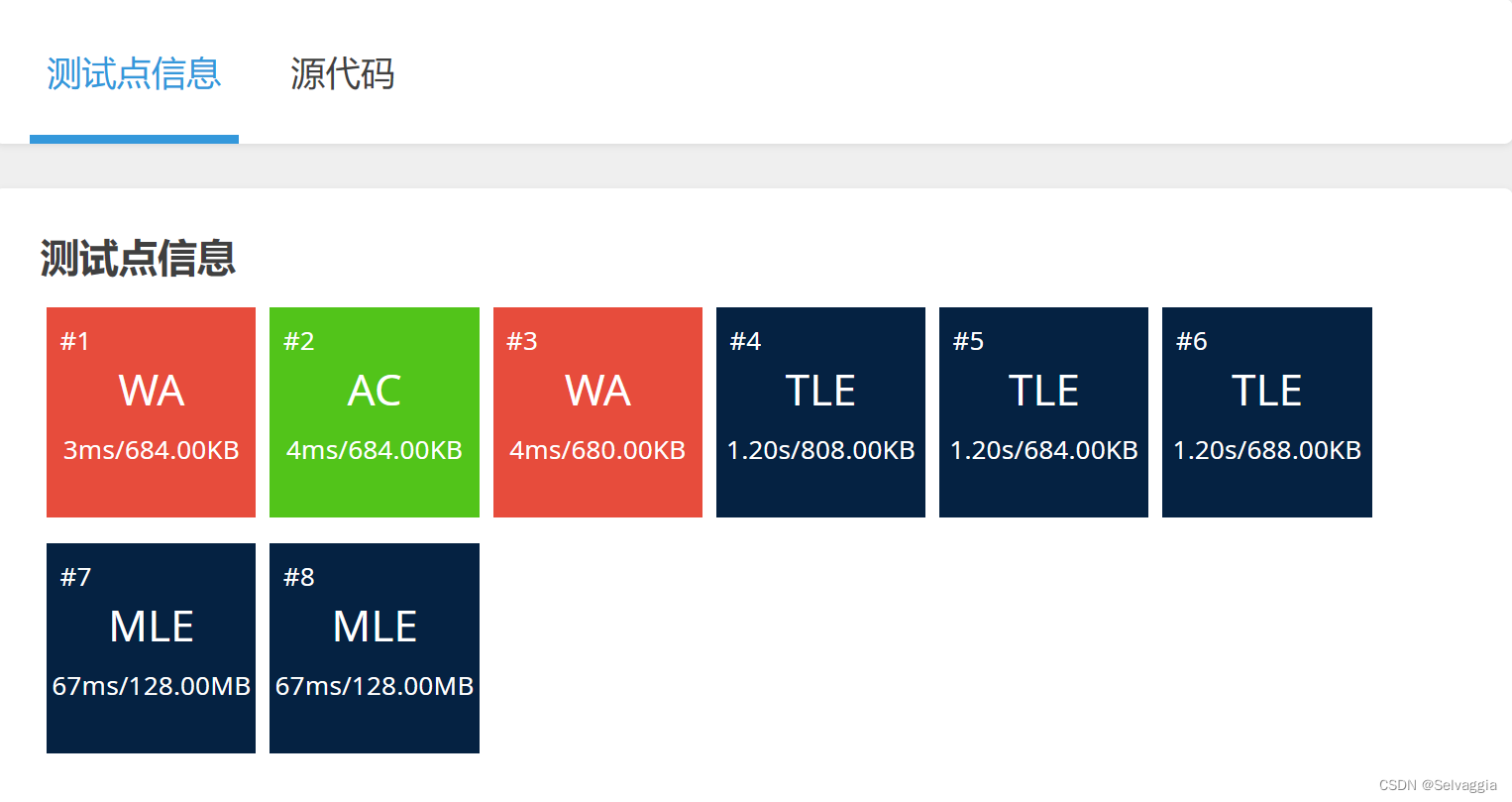
在这种解题方式上用快速幂有些多余。分枝过多的递归当n=100时,几乎不能在题目规定时间内计算出来。当n<100时,通过累乘的方式将4一次、一次乘给ans,这并不会对程序的效率造成很大影响。