统计学 一元线性回归
回归(Regression):假定因变量与自变量之间有某种关系,并把这种关系用适当的数学模型表达出来,利用该模型根据给定的自变量来预测因变量
-
线性回归:因变量和自变量之间是线性关系
-
非线性回归:因变量和自变量之间是非线性关系
变量间的关系
变量间的关系:往往分为函数关系和相关关系;函数关系是确定的关系(例如 y = x 2 y=x^2 y=x2 中 y y y 和 x x x 的关系),而相关关系是不确定的关系(例如家庭储蓄额和家庭收入)
相关系数:度量两个变量之间线性关系强度的统计量,样本相关系数记为
r
r
r (也称为 Pearson 相关系数),总体相关系数记为
ρ
\rho
ρ :
r
=
∑
(
X
−
X
ˉ
)
(
Y
−
Y
ˉ
)
∑
(
X
−
X
ˉ
)
2
⋅
∑
(
Y
−
Y
ˉ
)
2
r=\frac{\sum(X-\bar{X})(Y-\bar{Y})}{\sqrt{\sum(X-\bar{X})^2\cdot\sum(Y-\bar{Y})^2}}
r=∑(X−Xˉ)2⋅∑(Y−Yˉ)2∑(X−Xˉ)(Y−Yˉ)
- r ∈ [ − 1 , 1 ] r\in[-1,\,1] r∈[−1,1] ,越接近 1 1 1 代表两个变量之间正线性相关关系越强,越接近 − 1 -1 −1 代表两个变量之间负线性相关关系越强,等于 0 0 0 表示两个变量之间不存在线性关系;
- r r r 具有对称性,即 r X Y = r Y X r_{XY}=r_{YX} rXY=rYX ;很显然,若 X X X 与 Y Y Y 之间是线性关系,那么 Y Y Y 和 X X X 之间也是线性关系;
- r r r 不具有量纲,对 X X X 和 Y Y Y 的缩放不敏感,其数值大小与 X X X 和 Y Y Y 的尺度以及原点无关;
- r r r 不能用于描述非线性关系,可以结合散点图得出结论;
- r r r 是两个变量之间线性关系的度量,但不一定意味着 X X X 与 Y Y Y 有因果关系。
相关系数的检验:采用 R.A.Fisher 提出的 t 分布检验,既可用于小样本,也可用于大样本:
① 提出假设: H 0 H_0 H0 : ρ = 0 \rho=0 ρ=0 ; H 1 H_1 H1 : ρ = 1 \rho=1 ρ=1 ;
② 计算样本相关系数 r r r 以及检验统计量 t = r n − 2 1 − r 2 ∼ t ( n − 2 ) t=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}\sim t(n-2) t=1−r2rn−2∼t(n−2)
③ 算出 P P P 值,进行决策
一元线性回归模型的估计
一元回归:当回归分析只涉及一个自变量时称为一元回归
回归模型:描述因变量
y
y
y 如何依赖于自变量
x
x
x 和误差项
ε
\varepsilon
ε 的方程;一元线性回归模型可表示为:
y
=
β
0
+
β
1
x
+
ε
y=\beta_0+\beta_1x+\varepsilon
y=β0+β1x+ε
模型参数为
β
0
\beta_0
β0 和
β
1
\beta_1
β1 ;随机变量
ε
\varepsilon
ε 被称为误差项,对其需要作出以下假定:
- 正态性: ε \varepsilon ε 服从期望为 0 的正态分布;
- 方差齐性:对于所有的 X X X 值, ε \varepsilon ε 的方差值 σ 2 \sigma^2 σ2 都相同;
- 独立性:两个不同 X X X 值对应的 ε \varepsilon ε 不相关
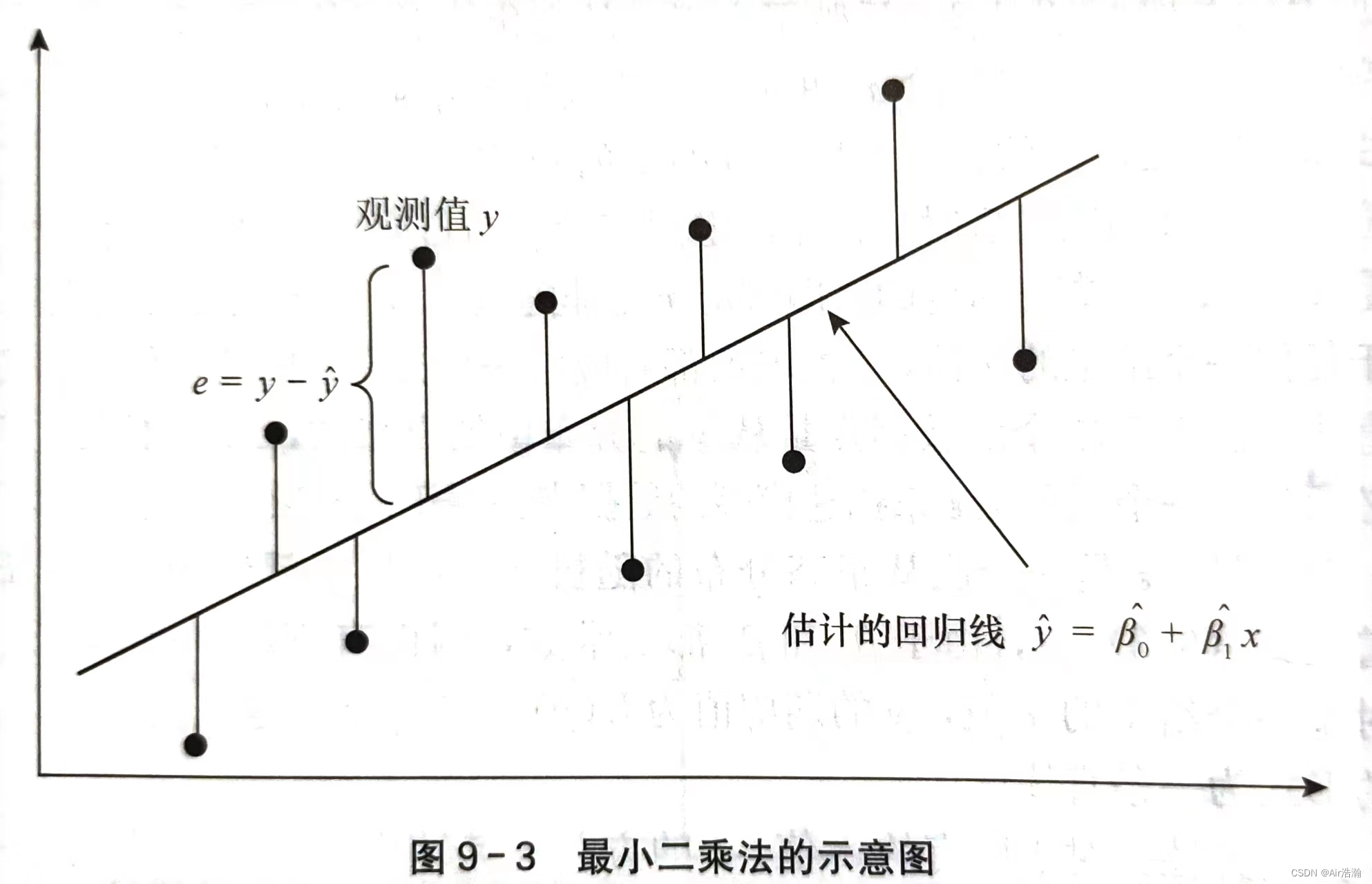
估计的回归方程:总体的 β 1 \beta_1 β1 和 β 0 \beta_0 β0 是未知的,需要用样本数据去估计,为: y ^ = β 0 ^ + β 1 ^ x \hat{y}=\hat{\beta_0}+\hat{\beta_1}x y^=β0^+β1^x ( β 1 ^ \hat{\beta_1} β1^ 称为回归系数)
最小二乘法:使离差
∣
y
^
−
y
∣
|\hat{y}-y|
∣y^−y∣ 的平方和最小的估计方法,即:
Q
=
∑
(
y
i
−
y
^
i
)
2
=
∑
(
y
i
−
β
^
0
−
β
1
^
x
i
)
2
=
m
i
n
Q=\sum(y_i-\hat{y}_i)^2=\sum(y_i-\hat{\beta}_0-\hat{\beta_1}x_i)^2=min
Q=∑(yi−y^i)2=∑(yi−β^0−β1^xi)2=min
求导得到:
{
∂
Q
∂
β
0
∣
β
0
=
β
^
0
=
−
2
∑
(
y
i
−
β
^
0
−
β
^
1
x
i
)
=
0
∂
Q
∂
β
1
∣
β
1
=
β
^
1
=
−
2
∑
x
i
(
y
i
−
β
^
0
−
β
^
1
x
i
)
=
0
\left\{ \begin{array}{l} \frac{\partial Q}{\partial \beta_0}\lvert_{\beta_0=\hat{\beta}_0}=-2\sum(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)=0 \\ \frac{\partial Q}{\partial \beta_1}\lvert_{\beta_1=\hat{\beta}_1}=-2\sum x_i(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)=0 \end{array} \right.
{∂β0∂Q∣β0=β^0=−2∑(yi−β^0−β^1xi)=0∂β1∂Q∣β1=β^1=−2∑xi(yi−β^0−β^1xi)=0
解得:
{
β
^
1
=
∑
(
x
−
x
ˉ
)
(
y
−
y
ˉ
)
∑
(
x
−
x
ˉ
)
2
β
0
^
=
y
ˉ
−
β
^
1
x
ˉ
\left\{ \begin{array}{l} \hat{\beta}_1=\frac{\sum(x-\bar{x})(y-\bar{y})}{\sum(x-\bar{x})^2} \\ \hat{\beta_0}=\bar{y}-\hat\beta_1\bar{x} \end{array} \right.
{β^1=∑(x−xˉ)2∑(x−xˉ)(y−yˉ)β0^=yˉ−β^1xˉ
(最小二乘法得到的回归直线通过样本平均点
(
x
ˉ
,
y
ˉ
)
(\bar{x},\,\bar{y})
(xˉ,yˉ) )
一元线性回归模型的判优
拟合优度:回归直线与各观测点的接近程度称为模型的的拟合优度,评价拟合优度的一个重要统计量就是决定系数
变差:因变量的取值的波动称为变差,变差的产生来自两个方面:
- 由于自变量的取值不同造成的
- 自变量以外的随机因素的影响
总平方和:
n
n
n 次观测值的总变差可以由这些变差的平方和来表示,称为总平方和(SST),
S
S
T
=
∑
(
y
i
−
y
ˉ
)
2
SST=\sum(y_i-\bar{y})^2
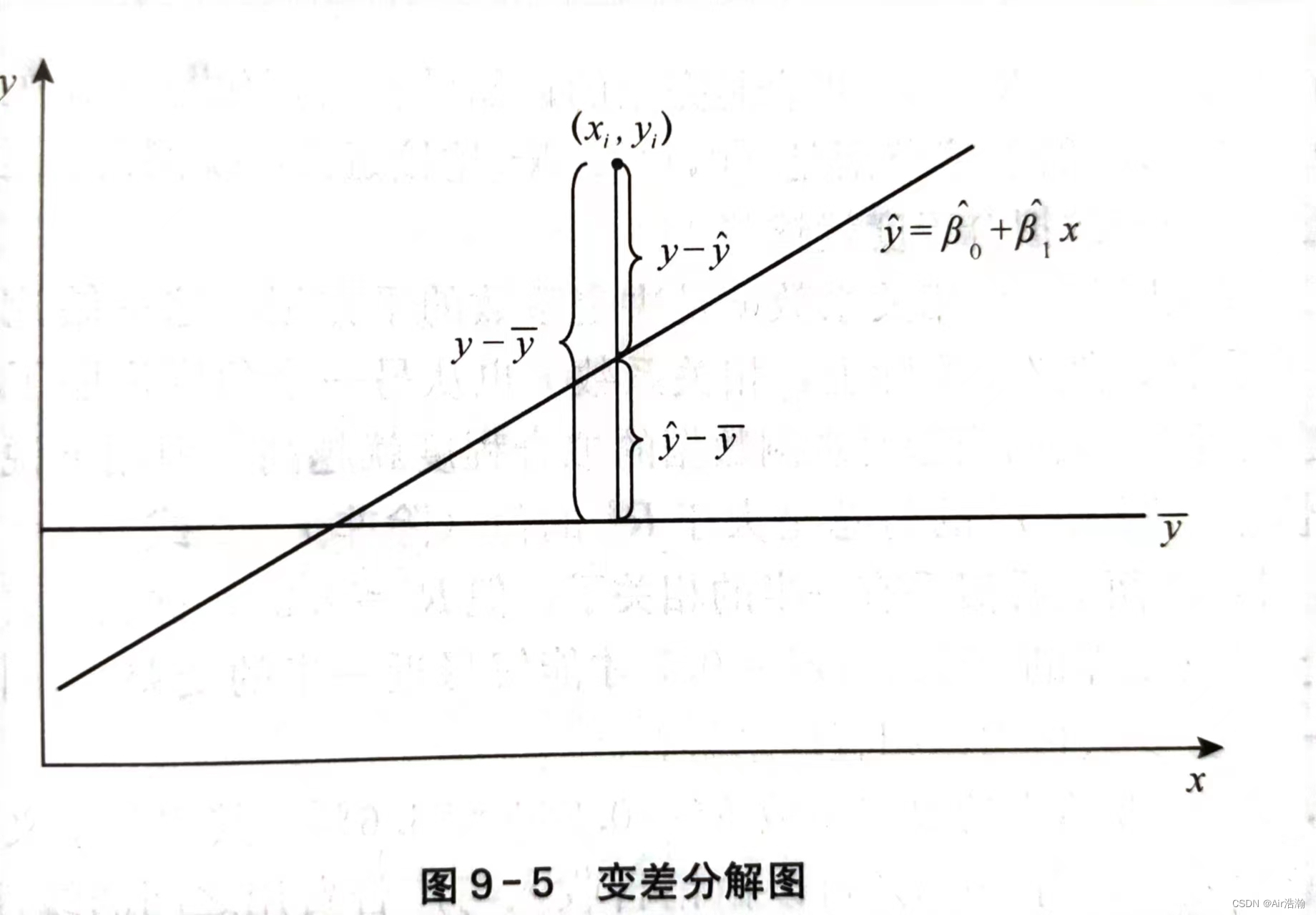
SST=∑(yi−yˉ)2 ;总平方和可以分解为:
S
S
T
=
∑
(
y
i
−
y
^
i
+
y
^
i
−
y
ˉ
)
2
=
∑
(
y
i
−
y
^
i
)
2
+
∑
(
y
^
i
−
y
ˉ
)
2
−
2
∑
(
y
i
−
y
^
i
)
(
y
^
i
−
y
ˉ
)
SST=\sum(y_i-\hat{y}_i+\hat{y}_i-\bar{y})^2=\sum(y_i-\hat{y}_i)^2+\sum(\hat{y}_i-\bar{y})^2-2\sum(y_i-\hat{y}_i)(\hat{y}_i-\bar{y})
SST=∑(yi−y^i+y^i−yˉ)2=∑(yi−y^i)2+∑(y^i−yˉ)2−2∑(yi−y^i)(y^i−yˉ)
可以证明
2
∑
(
y
i
−
y
^
i
)
(
y
^
i
−
y
ˉ
)
=
0
2\sum(y_i-\hat{y}_i)(\hat{y}_i-\bar{y})=0
2∑(yi−y^i)(y^i−yˉ)=0 ,所以总平方和实际上表现为两个部分:
{
S
S
T
=
∑
(
y
i
−
y
^
i
)
2
+
∑
(
y
^
i
−
y
ˉ
)
2
S
S
R
=
∑
(
y
^
i
−
y
ˉ
)
2
S
S
E
=
∑
(
y
i
−
y
^
i
)
2
\left \{ \begin{array}{l} SST=\sum(y_i-\hat{y}_i)^2+\sum(\hat{y}_i-\bar{y})^2 \\ SSR=\sum(\hat{y}_i-\bar{y})^2 \\ SSE=\sum(y_i-\hat{y}_i)^2\\ \end{array} \right.
⎩
⎨
⎧SST=∑(yi−y^i)2+∑(y^i−yˉ)2SSR=∑(y^i−yˉ)2SSE=∑(yi−y^i)2
- 回归平方和(SSR):反映了 y y y 的总变差中由于 x x x 和 y y y 的线性关系引起的 y y y 的变化部分,是可以由回归直线来解释的 y i y_i yi 的变差部分
- 残差平方和(SSE) :是实际观测点与回归值的离差平方和,表示除了 x x x 对 y y y 的线性影响之外的其他随机因素对 y y y 的影响
决定系数:又称判定系数,记为
R
2
R^2
R2 模型拟合的好坏取决于回归平方和 SSR 占总平方和 SST 的比例,越大则直线拟合得越好:
R
2
=
S
S
R
S
S
T
=
∑
(
y
^
i
−
y
ˉ
)
2
∑
(
y
i
−
y
ˉ
)
2
R^2=\frac{SSR}{SST}=\frac{\sum(\hat{y}_i-\bar{y})^2}{\sum(y_i-\bar{y})^2}
R2=SSTSSR=∑(yi−yˉ)2∑(y^i−yˉ)2
在一元线性回归中,相关系数 r r r 是决定系数 R 2 R^2 R2 的平方根
估计标准误差:即残差的标准差
s
e
s_e
se,是对误差项
ε
\varepsilon
ε 的标准差
σ
\sigma
σ 的估计,反映了实际观测值
y
i
y_i
yi 与回归估计值
y
^
i
\hat{y}_i
y^i 之间的差异程度,
s
e
s_e
se 越小,则直线拟合得越好:
s
e
=
S
S
E
n
−
2
=
∑
(
y
i
−
y
^
i
)
2
n
−
2
s_e=\sqrt{\frac{SSE}{n-2}}=\sqrt{\frac{\sum(y_i-\hat{y}_i)^2}{n-2}}
se=n−2SSE=n−2∑(yi−y^i)2
一元线性回归模型的显著性检验
线性关系检验
线性关系检验:也称为 F F F 检验,用于检验自变量 x x x 和因变量 y y y 之间的线性关系是否显著,它们的关系是否能用一个线性模型 y = β 0 + β 1 x + ε y=\beta_0+\beta_1x+\varepsilon y=β0+β1x+ε 来表示。
- SSR 的自由度为自变量 k k k (这里一元线性回归所以 k = 1 k=1 k=1 ),其除以自由度后得到回归均方(MSR)
- SSE 的自由度为 n − k − 1 n-k-1 n−k−1 (这里一元线性回归所以 n − 2 n-2 n−2),其除以自由度后得到残差均方(MSE)
① 提出检验假设:
- H 0 H_0 H0 : β 1 = 0 \beta_1=0 β1=0 (两个变量之间的线性关系不显著)
- H 1 H_1 H1 : β 1 ≠ 0 \beta_1\not=0 β1=0 (两个变量之间的线性关系显著)
② 计算检验自变量为
F
=
S
S
R
/
1
S
S
E
/
(
n
−
2
)
=
M
S
R
M
S
E
∼
F
(
1
,
n
−
2
)
F=\frac{SSR/1}{SSE/(n-2)}=\frac{MSR}{MSE}\sim F(1,\,n-2)
F=SSE/(n−2)SSR/1=MSEMSR∼F(1,n−2)
③ 做出决策,确定显著性水平
α
\alpha
α ,根据自由度
d
f
1
=
1
df_1=1
df1=1 和
d
f
2
=
n
−
2
df_2=n-2
df2=n−2 得到
P
P
P 值,与
α
\alpha
α 进行比较
回归系数的检验和推断
回归系数检验:也称为 t 检验,用于检验自变量对因变量的影响是否显著;在一元线性回归模型中,回归系数检验和线性关系检验等价,而在多元线性回归中这两种检验不再等价。其检验假设为:
- H 0 H_0 H0 : β 1 = 0 \beta_1=0 β1=0 (自变量对因变量的影响不显著)
- H 1 H_1 H1 : β 1 ≠ 0 \beta_1\not=0 β1=0 (自变量对因变量的影响显著)
β
1
^
\hat{\beta_1}
β1^ 和
β
0
^
\hat{\beta_0}
β0^ 也是随机变量,它们有自己的抽样分布,统计证明,
β
1
^
\hat{\beta_1}
β1^ 服从正态分布,期望
E
(
β
1
^
)
=
β
1
E(\hat{\beta_1})=\beta_1
E(β1^)=β1 ,标准差的估计量为:(
s
e
s_e
se 为估计标准误差)
s
β
1
^
=
s
e
∑
x
i
2
−
1
n
(
∑
x
i
)
2
s_{\hat{\beta_1}}=\frac{s_e}{\sqrt{\sum x_i^2-\frac{1}{n}(\sum x_i)^2}}
sβ1^=∑xi2−n1(∑xi)2se
(这个 s β 1 ^ s_{\hat{\beta_1}} sβ1^ 的分母太搞了,实际上等价于 s β ^ 1 = s e ∑ ( x i − x ˉ ) 2 s_{\hat{\beta}_1}=\frac{s_e}{\sqrt{\sum(x_i-\bar{x})^2}} sβ^1=∑(xi−xˉ)2se )
将回归系数标准化,就可以得到用于检验回归系数
β
1
^
\hat{\beta_1}
β1^ 的统计量
t
t
t ,在原假设成立的条件下,
β
1
^
−
β
1
=
β
1
^
\hat{\beta_1}-\beta_1=\hat{\beta_1}
β1^−β1=β1^ ,因此检验统计量为:
t
=
β
1
^
s
β
1
^
∼
t
(
n
−
2
)
t=\frac{\hat{\beta_1}}{s_{\hat{\beta_1}}}\sim t(n-2)
t=sβ1^β1^∼t(n−2)
除了对回归系数进行检验外,还可以得到置信区间,回归系数
β
1
\beta_1
β1 在置信水平为
1
−
α
1-\alpha
1−α 下的置信区间为:
(
β
1
^
±
t
α
/
2
(
n
−
2
)
s
e
∑
(
x
i
−
x
ˉ
)
2
)
\left( \hat{\beta_1}\pm t_{\alpha/2}(n-2)\frac{s_e}{\sqrt{\sum(x_i-\bar{x})^2}} \right)
(β1^±tα/2(n−2)∑(xi−xˉ)2se)
还可以得到截距
β
0
\beta_0
β0 的
1
−
α
1-\alpha
1−α 置信区间为:
(
β
0
^
±
t
α
/
2
(
n
−
2
)
s
e
1
n
+
x
ˉ
∑
(
x
i
−
x
ˉ
)
2
)
\left( \hat{\beta_0}\pm t_{\alpha/2}(n-2)s_e\sqrt{\frac{1}{n}+\frac{\bar{x}}{\sum(x_i-\bar{x})^2}} \right)
(β0^±tα/2(n−2)sen1+∑(xi−xˉ)2xˉ)
利用回归方程进行预测
回归分析的目的:根据所建立的回归方程,用给定的自变量来预测因变量。如果对于 x x x 的一个给定值 x 0 x_0 x0 ,求出 y y y 的一个预测值 y ^ 0 \hat{y}_0 y^0 ,就是点估计;若是求出 y 0 y_0 y0 的一个估计区间,就是个别值的区间估计;若是求出 y 0 ˉ \bar{y_0} y0ˉ 的一个估计区间,就是平均值的区间估计。
例如,我们收集数据研究许多家企业的广告费支出作为自变量对销售收入这个因变量造成的影响:
- 求出广告费用为 200 万元时企业销售收入平均值的区间估计,就是平均值的区间估计;
- 求出广告费用为 200 万元的那家企业销售收入的区间估计,就是个别值的区间估计
点估计
点估计很明显,就是直接将 x 0 x_0 x0 代入方程即可,接下来介绍平均值和个别值的预测区间。
平均值的置信区间
平均值的置信区间 :设给定因变量
x
x
x 的一个值
x
0
x_0
x0 ,
E
(
y
0
)
E(y_0)
E(y0) 为给定
x
0
x_0
x0 时因变量
y
y
y 的期望值。当
x
=
x
0
x=x_0
x=x0 时,
y
^
0
=
β
0
^
+
β
1
^
x
0
\hat{y}_0=\hat{\beta_0}+\hat{\beta_1}x_0
y^0=β0^+β1^x0 就是
E
(
y
0
)
E(y_0)
E(y0) 的估计值。那么按照区间估计的公式,要知道
y
0
^
\hat{y_0}
y0^ 的标准差的估计量
s
y
0
^
s_{\hat{y_0}}
sy0^ :
s
y
0
^
=
s
e
1
n
+
(
x
0
−
x
ˉ
)
2
∑
(
x
i
−
x
ˉ
)
2
s_{\hat{y_0}}=s_e\sqrt{\frac{1}{n}+\frac{(x_0-\bar{x})^2}{\sum{(x_i-\bar{x})^2}}}
sy0^=sen1+∑(xi−xˉ)2(x0−xˉ)2
因此,对于给定的
x
0
x_0
x0,平均值
E
(
y
0
)
E(y_0)
E(y0) 在
1
−
α
1-\alpha
1−α 置信水平下的置信区间为:
(
y
0
^
±
t
α
/
2
(
n
−
2
)
s
e
1
n
+
(
x
0
−
x
ˉ
)
2
∑
(
x
i
−
x
ˉ
)
)
\left( \hat{y_0}\pm t_{\alpha/2}(n-2)s_e\sqrt{\frac{1}{n}+\frac{(x_0-\bar{x})^2}{\sum(x_i-\bar{x})}} \right)
(y0^±tα/2(n−2)sen1+∑(xi−xˉ)(x0−xˉ)2)
当
x
0
=
x
ˉ
x_0=\bar{x}
x0=xˉ 时,
y
^
0
\hat{y}_0
y^0 的标准差的估计量最小,此时有
s
y
^
0
=
s
e
1
n
s_{\hat{y}_0}=s_e\sqrt{\frac{1}{n}}
sy^0=sen1 ,也就是说当
x
0
=
x
ˉ
x_0=\bar{x}
x0=xˉ 时,估计是最准确的。
x
0
x_0
x0 偏离
x
ˉ
\bar{x}
xˉ 越远,那么
y
0
y_0
y0 的平均值的置信区间就变得越宽,估计的效果也就越不好。
个别值的预测区间
个别值的预测区间:用
s
i
n
d
s_{ind}
sind 表示估计
y
y
y 的一个个别值时
y
0
^
\hat{y_0}
y0^ 的标准差的估计量:
s
i
n
d
=
s
e
1
+
1
n
+
(
x
0
−
x
ˉ
)
2
∑
(
x
i
−
x
ˉ
)
2
s_{ind}=s_e\sqrt{1+\frac{1}{n}+\frac{(x_0-\bar{x})^2}{\sum{(x_i-\bar{x})^2}}}
sind=se1+n1+∑(xi−xˉ)2(x0−xˉ)2
因此,对于给定的
x
0
x_0
x0 ,
y
y
y 的一个个别值
y
0
y_0
y0 在
1
−
α
1-\alpha
1−α 置信水平下的预测区间为:
(
y
0
^
±
t
α
/
2
(
n
−
2
)
s
e
1
+
1
n
+
(
x
0
−
x
ˉ
)
2
∑
(
x
i
−
x
ˉ
)
)
\left( \hat{y_0}\pm t_{\alpha/2}(n-2)s_e\sqrt{1+\frac{1}{n}+\frac{(x_0-\bar{x})^2}{\sum(x_i-\bar{x})}} \right)
(y0^±tα/2(n−2)se1+n1+∑(xi−xˉ)(x0−xˉ)2)
相比于置信区间而言,预测区间范围更宽一些,因此估计
y
y
y 的平均值比预测
y
y
y 的一个个别值更准确一些。同样,当
x
0
=
x
ˉ
x_0=\bar{x}
x0=xˉ 时,两个区间也都是最准确的。
用残差检验模型的假定
残差: e = y i − y ^ i e=y_i-\hat{y}_i e=yi−y^i ,表示用估计的回归方程去预测 y i y_i yi 而引起的误差
残差分析:跟方差分析一样,我们在做一元回归分析的时候也假定 y = β 0 + β 1 x + ε y=\beta_0+\beta_1x+\varepsilon y=β0+β1x+ε 中的误差项 ε \varepsilon ε 是期望为零、具有方差齐性且相互独立的正态分布随机变量,需要对这个假设能否成立进行分析。
残差图:检验误差项 ε \varepsilon ε 是否满足这些假设,可以通过对残差图的分析来完成。常用的残差图有关于 x x x 的残差图、标准化残差图等。
- 关于 x x x 的残差图是用横坐标表示自变量 x i x_i xi 的值,纵轴表示对应的残差 e i e_i ei
检验方差齐性
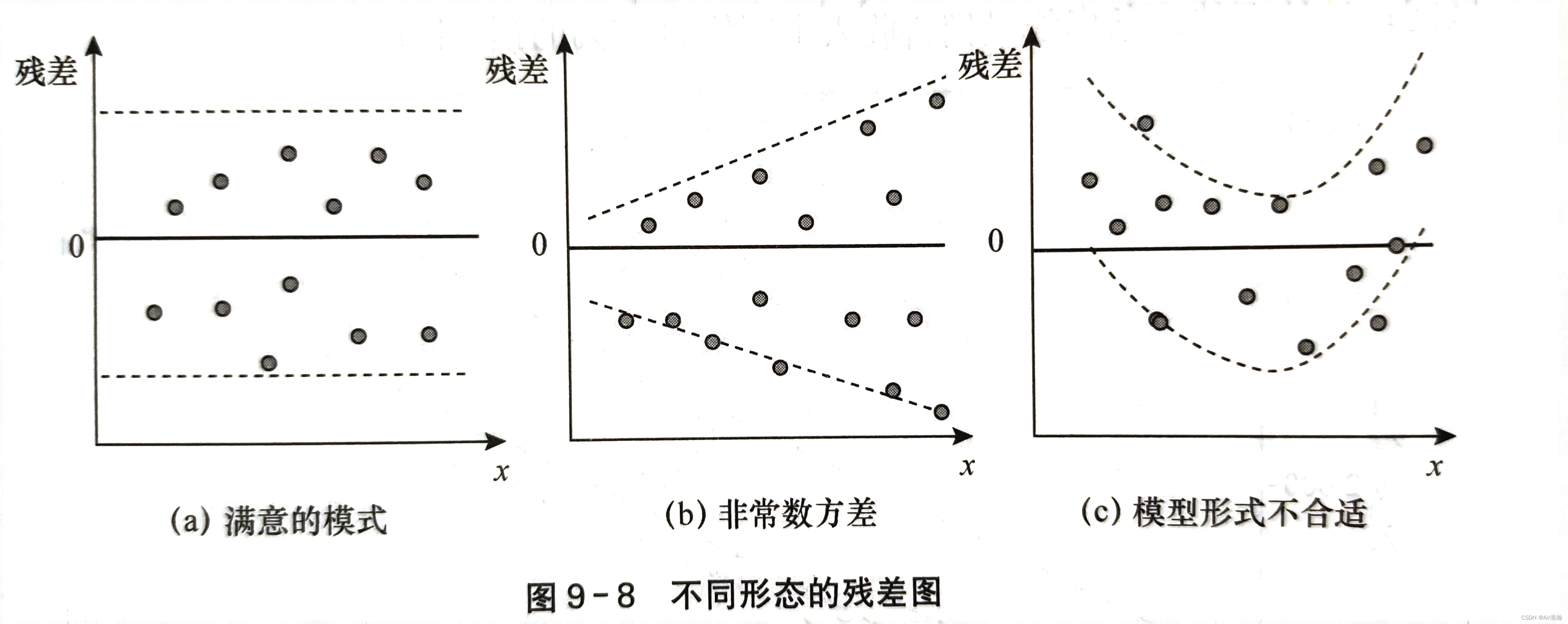
如果满足方差齐性,则残差图中的所有点都应当落在同一水平带中(图 a)且没有固定的模式,否则称为异方差性(图 b)。如果出现图 c 的情况,那么应当考虑非线性回归:
检验正态性
标准化残差:也称 Pearson 残差或半 t 化残差,是残差除以其标准差后得到的结果:
z
e
i
=
e
i
s
e
=
y
i
−
y
^
i
s
e
z_{e_i}=\frac{e_i}{s_e}=\frac{y_i-\hat{y}_i}{s_e}
zei=seei=seyi−y^i
关于正态性的检验可以用标准化残差分析来完成。如果
ε
\varepsilon
ε 服从正态分布,那么标准化残差的分布也应服从正态分布。例如,标准化后,应当有
95
%
95\%
95% 的残差都落在
[
−
2
,
2
]
[-2,2]
[−2,2] 之间:
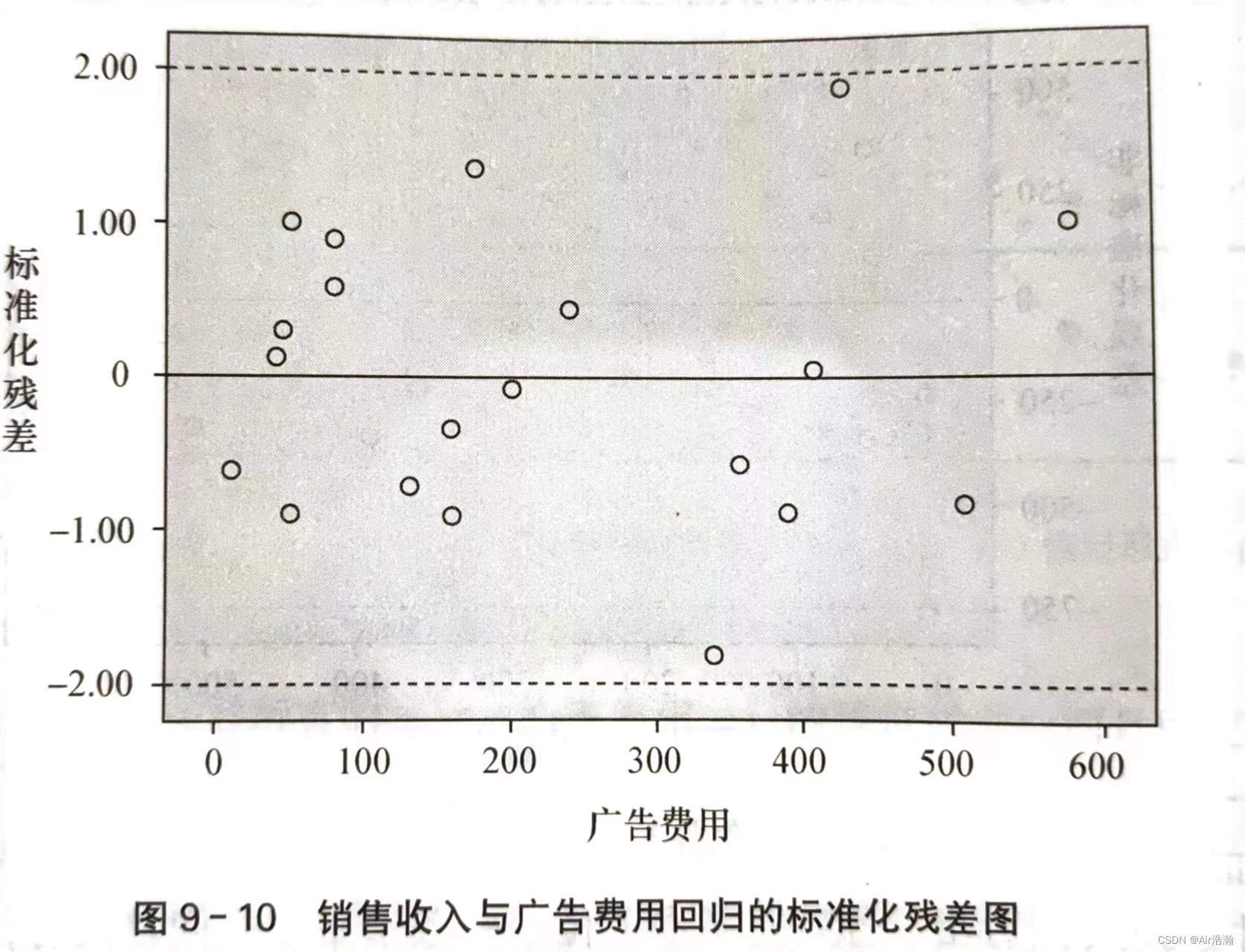
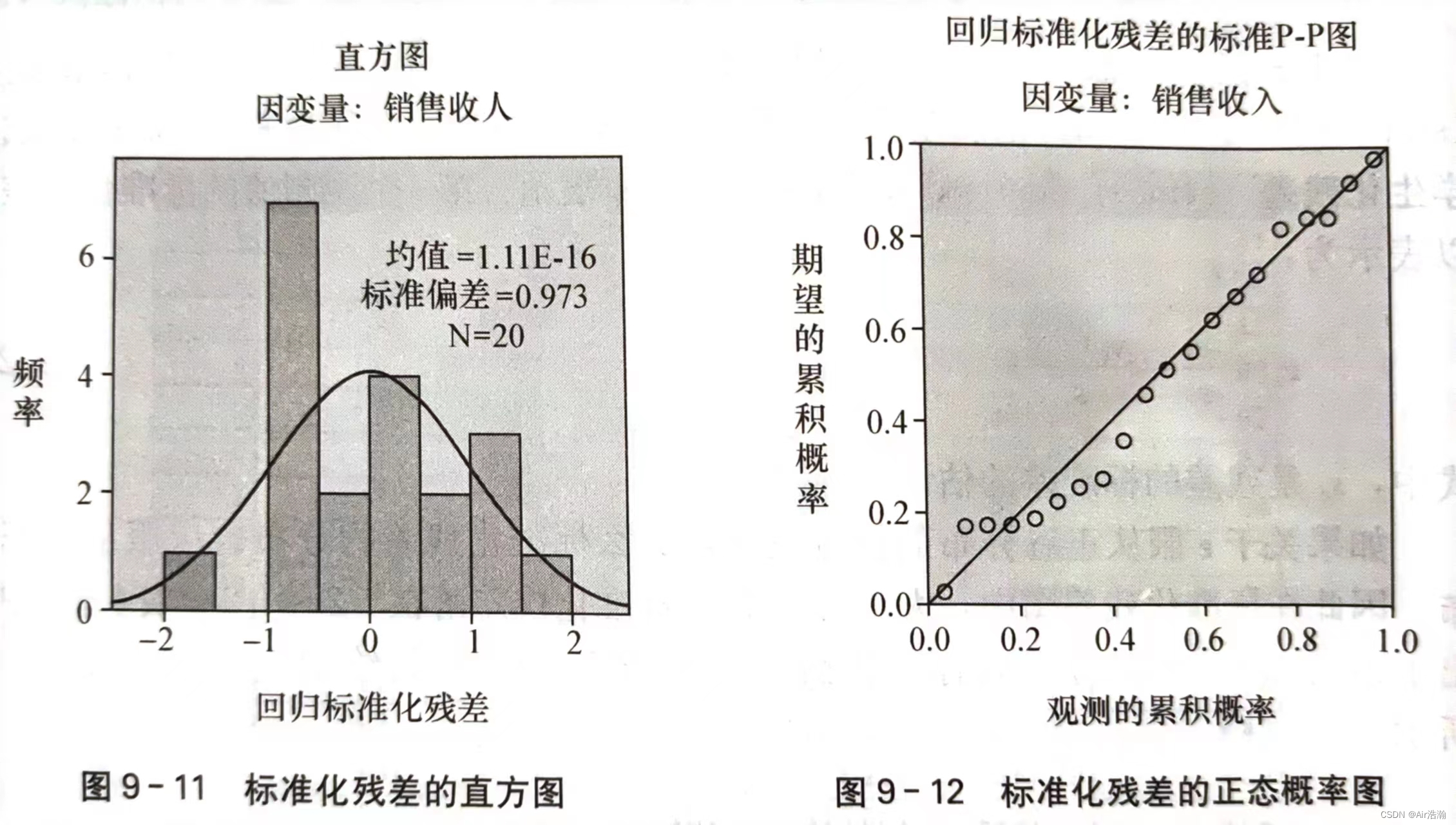
也可以画直方图或者 P-P 图来检验: