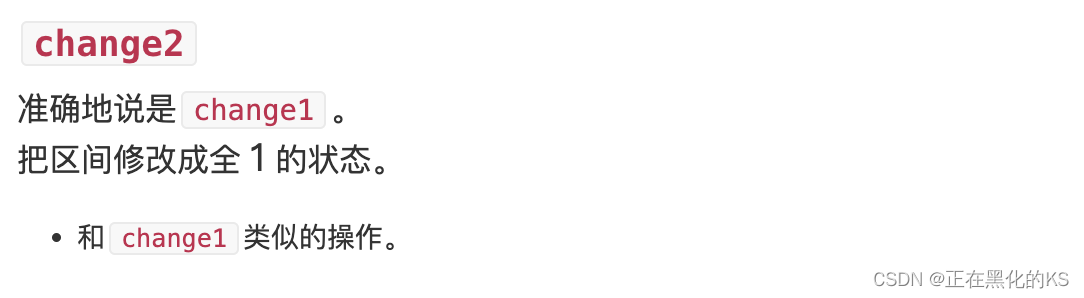Acwing：一道关于线段树的好题（有助于全面理解线段树）

news2025/8/2 11:09:28

题目链接🔗：2643. 序列操作 - AcWing题库

前驱知识：需要理解线段树的结构和程序基本框架、以及懒标记的操作。

题目描述

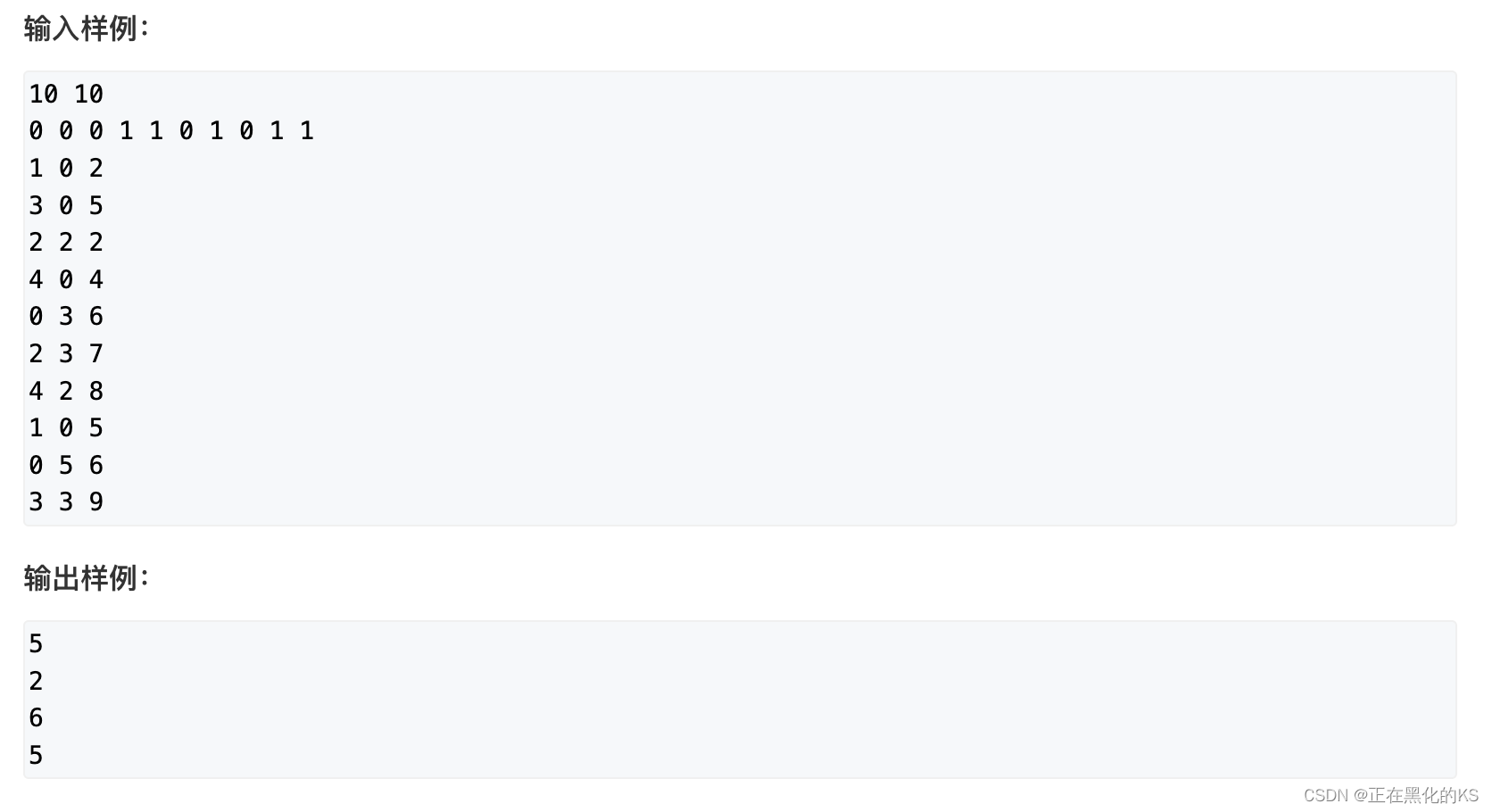
题目分析

对区间在线进行修改和查询，一般就是用线段树来解决，观察到题目一共有五个操作：

我们首先要思考需要用线段树维护哪些信息，通过维护这些信息，在查询时能够得到需要的答案。

根据查询的内容，我们发现需要维护区间内1的个数 $sum1$ ，以及区间内最多连续1的个数 $m1$

由于题目的操作对象就是0和1，我们可以想到对称维护0和1的信息（主要是因为存在操作2

那么综合来看，我们可以维护线段树的以下信息：

$l$ ：区间左端点

$r$ ：区间右端点

$sum1$ ：区间内1的个数

$sum0$ ：区间内0的个数

$l1$ ：区间内左边最多连续1的个数

$l0$ ：区间内左边最多连续0的个数

$r1$ ：区间内右边最多连续1的个数

$r0$ ：区间内右边最多连续0的个数

$m0$ ：区间内最长连续0的个数

$m1$ ：区间内最长连续1的个数

$flag0$ ：操作0对应的懒标记

$flag1$ ：操作1对应的懒标记

$rev$ ：操作2对应的懒标记

具体维护方案如下

AC代码

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std ;

const int N = 1e5 + 10 ; 

int n, m, a[N] ; 
struct Node 
{
    int l, r ; 
    int sum0, sum1, l0, l1, r0, r1, m0, m1 ; 
    bool flag0, flag1, rev ; 
}tr[4 * N] ; 

void pushup(int u) 
{
    tr[u].sum0 = tr[u << 1].sum0 + tr[u << 1 | 1].sum0 ; 
    tr[u].sum1 = tr[u << 1].sum1 + tr[u << 1 | 1].sum1 ;
    tr[u].l0 = (tr[u << 1].sum1) ? tr[u << 1].l0 : tr[u << 1].sum0 + tr[u << 1 | 1].l0 ;
    tr[u].l1 = (tr[u << 1].sum0) ? tr[u << 1].l1 : tr[u << 1].sum1 + tr[u << 1 | 1].l1 ;
    tr[u].r0 = (tr[u << 1 | 1].sum1) ? tr[u << 1 | 1].r0 :  tr[u << 1 | 1].sum0 + tr[u << 1].r0 ; 
    tr[u].r1 = (tr[u << 1 | 1].sum0) ? tr[u << 1 | 1].r1 :  tr[u << 1 | 1].sum1 + tr[u << 1].r1 ;
    tr[u].m0 = max(max(tr[u << 1].m0, tr[u << 1 | 1].m0), tr[u << 1].r0 + tr[u << 1 | 1].l0) ;
    tr[u].m1 = max(max(tr[u << 1].m1, tr[u << 1 | 1].m1), tr[u << 1].r1 + tr[u << 1 | 1].l1) ;
}

void pushup_Node(Node &root, Node ls, Node rs) 
{
    root.sum0 = ls.sum0 + rs.sum0 ; 
    root.sum1 = ls.sum1 + rs.sum1 ; 
    root.l0 = (ls.sum1) ? ls.l0 : ls.sum0 + rs.l0 ; 
    root.l1 = (ls.sum0) ? ls.l1 : ls.sum1 + rs.l1 ; 
    root.r0 = (rs.sum1) ? rs.r0 : rs.sum0 + ls.r0 ; 
    root.r1 = (rs.sum0) ? rs.r1 : rs.sum1 + ls.r1 ;
    root.m0 = max(max(ls.m0, rs.m0), ls.r0 + rs.l0) ; 
    root.m1 = max(max(ls.m1, rs.m1), ls.r1 + rs.l1) ;
}

void pushdown(int u) 
{
    if (tr[u].flag0) 
    {
        tr[u << 1].sum0 = tr[u << 1].l0 = tr[u << 1].r0 = tr[u << 1].m0 = tr[u << 1].r - tr[u << 1].l + 1 ; 
        tr[u << 1 | 1].sum0 = tr[u << 1 | 1].l0 = tr[u << 1 | 1].r0 = tr[u << 1 | 1].m0 = tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1 ;
        tr[u << 1].sum1 = tr[u << 1].l1 = tr[u << 1].r1 = tr[u << 1].m1 = 0 ; 
        tr[u << 1 | 1].sum1 = tr[u << 1 | 1].l1 = tr[u << 1 | 1].r1 = tr[u << 1 | 1].m1 = 0 ; 
        tr[u << 1].flag0 = tr[u << 1 | 1].flag0 = true ; 
        tr[u << 1].flag1 = tr[u << 1 | 1].flag1 = tr[u << 1].rev = tr[u << 1 | 1].rev = false ;
        tr[u].flag0 = false ; 
    }
    if (tr[u].flag1) {
        tr[u << 1].sum1 = tr[u << 1].l1 = tr[u << 1].r1 = tr[u << 1].m1 = tr[u << 1].r - tr[u << 1].l + 1 ; 
        tr[u << 1 | 1].sum1 = tr[u << 1 | 1].l1 = tr[u << 1 | 1].r1 = tr[u << 1 | 1].m1 = tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1 ;
        tr[u << 1].sum0 = tr[u << 1].l0 = tr[u << 1].r0 = tr[u << 1].m0 = 0 ;
        tr[u << 1 | 1].sum0 = tr[u << 1 | 1].l0 = tr[u << 1 | 1].r0 = tr[u << 1 | 1].m0 = 0 ;
        tr[u << 1].flag1 = tr[u << 1 | 1].flag1 = true ;
        tr[u << 1 | 1].flag0 = tr[u << 1 | 1].flag0 = tr[u << 1].rev = tr[u << 1 | 1].rev = false ;
        tr[u].flag1 = false ;
    }
    if (tr[u].rev) 
    {
        swap(tr[u << 1].sum0, tr[u << 1].sum1) ;
        swap(tr[u << 1 | 1].sum0, tr[u << 1 | 1].sum1) ;
        
        swap(tr[u << 1].l0, tr[u << 1].l1) ; 
        swap(tr[u << 1 | 1].l0, tr[u << 1 | 1].l1) ;
        
        swap(tr[u << 1].r0, tr[u << 1].r1) ; 
        swap(tr[u << 1 | 1].r0, tr[u << 1 | 1].r1) ;
        
        swap(tr[u << 1].m0, tr[u << 1].m1) ; 
        swap(tr[u << 1 | 1].m0, tr[u << 1 | 1].m1) ;
        
        tr[u << 1].rev ^= 1, tr[u << 1 | 1].rev ^= 1 ; 
        tr[u].rev = 0 ;
    }
}

void build(int u, int l, int r) 
{
    tr[u].l = l, tr[u].r = r ; 
    if (l == r) 
    {
        tr[u].sum0 = tr[u].l0 = tr[u].r0 = tr[u].m0 = a[r] ^ 1 ; 
        tr[u].sum1 = tr[u].l1 = tr[u].r1 = tr[u].m1 = a[r] & 1 ; 
        return ; 
    }
    int mid = l + r >> 1 ;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r) ; 
    pushup(u) ; 
}

void change1(int u, int l, int r) 
{
    if (tr[u].l >= l && tr[u].r <= r) 
    {
        tr[u].sum1 = tr[u].l1 = tr[u].r1 = tr[u].m1 = 0 ; 
        tr[u].sum0 = tr[u].l0 = tr[u].r0 = tr[u].m0 = tr[u].r - tr[u].l + 1 ; 
        tr[u].flag0 = true, tr[u].flag1 = tr[u].rev = false ;
        return ;
    }
    pushdown(u) ; 
    int mid = tr[u].l + tr[u].r >> 1 ; 
    if (l <= mid) change1(u << 1, l, r) ; 
    if (r > mid) change1(u << 1 | 1, l, r) ; 
    pushup(u) ;
}

void change2(int u, int l, int r) 
{
    if (tr[u].l >= l && tr[u].r <= r) 
    {
        tr[u].sum0 = tr[u].l0 = tr[u].r0 = tr[u].m0 = 0 ; 
        tr[u].sum1 = tr[u].l1 = tr[u].r1 = tr[u].m1 = tr[u].r - tr[u].l + 1 ; 
        tr[u].flag1 = true, tr[u].flag0 = tr[u].rev = false ;
        return ;
    }
    pushdown(u) ; 
    int mid = tr[u].l + tr[u].r >> 1 ; 
    if (l <= mid) change2(u << 1, l, r) ; 
    if (r > mid) change2(u << 1 | 1, l, r) ; 
    pushup(u) ; 
}

void Reverse(int u, int l, int r) 
{
    if (tr[u].l >= l && tr[u].r <= r) 
    {
        swap(tr[u].sum0, tr[u].sum1) ; 
        swap(tr[u].l0, tr[u].l1) ; 
        swap(tr[u].r0, tr[u].r1) ; 
        swap(tr[u].m0, tr[u].m1) ; 
        tr[u].rev ^= 1 ; 
        return ; 
    }
    pushdown(u) ; 
    int mid = tr[u].l + tr[u].r >> 1 ; 
    if (l <= mid) Reverse(u << 1, l, r) ; 
    if (r > mid) Reverse(u << 1 | 1, l, r) ;
    pushup(u) ; 
}

int ask1(int u, int l, int r) 
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum1 ; 
    
    pushdown(u) ; 
    int mid = tr[u].l + tr[u].r >> 1 ; 
    int sum = 0 ; 
    if (l <= mid) sum = ask1(u << 1, l, r) ; 
    if (r > mid) sum += ask1(u << 1 | 1, l, r) ; 
    
    return sum ;
}

Node ask2(int u, int l, int r) 
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u] ; 
    
    pushdown(u) ; 
    int mid = tr[u].l + tr[u].r >> 1 ; 
    
    Node res ; 
    if (l > mid) return ask2(u << 1 | 1, l, r) ; 
    if (r <= mid) return ask2(u << 1, l, r) ; 
    
    Node ls = ask2(u << 1, l, r), rs = ask2(u << 1 | 1, l, r) ; 
    pushup_Node(res, ls, rs) ; 
    
    return res ; 
}

int main() 
{
    ios::sync_with_stdio(false) ; 
    cin >> n >> m ; 
    for (int i = 1 ; i <= n ; i ++ ) 
        cin >> a[i] ;
        
    build(1, 1, n) ; 
    
    while (m -- ) 
    {
        int opt, l, r ; 
        cin >> opt >> l >> r ; 
        l ++, r ++ ; 
        
        if (opt == 0) change1(1, l, r) ; 
        else if (opt == 1) change2(1, l, r) ; 
        else if (opt == 2) Reverse(1, l, r) ; 
        else if (opt == 3) cout << ask1(1, l , r) << endl ;
        else cout << ask2(1, l, r).m1 << endl ; 
    }

    return 0 ; 
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/394420.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！