题目

leetcode题目地址

给定一个不重复的整数数组 nums 。最大二叉树可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的子数组前缀上构建左子树。
递归地在最大值右边的子数组后缀上构建右子树。
返回 nums 构建的最大二叉树。

示列1

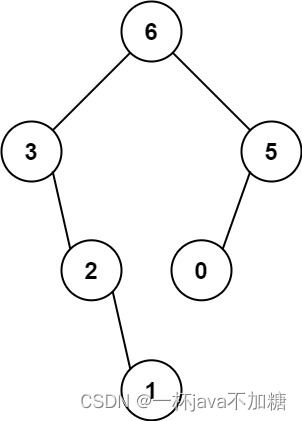
在这里插入图片描述

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示列2

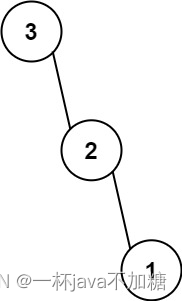
在这里插入图片描述

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数互不相同

code

递归：

确定函数的参数和返回值。参数是数组，返回值是节点。
确定递归终止条件。当没有元素时，返回null；当只有一个元素时，证明是叶子节点了，返回该节点。
找出每一次递归的逻辑。
找出最大值的下标，将最大值作为根节点，根据最大值下标划分区别。最大值下标左边，构造左子树；最大值下标右边，构造右子树。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return constructMaximumBinaryTreeRec(nums,0,nums.length);
    }

    public TreeNode constructMaximumBinaryTreeRec(int[] nums,int leftIndex,int rightIndex){
        // 没有元素了
        if(rightIndex - leftIndex <1){
            return null;
        }
        // 只有一个元素了
        if(rightIndex-leftIndex == 1){
            return new TreeNode(nums[leftIndex]);
        }
        int maxIndex = leftIndex; // 最大值的索引位置
        int maxVal = nums[maxIndex]; // 最大值
        for(int i=leftIndex+1;i<rightIndex;i++){
            if(nums[i]>maxVal){
                maxVal = nums[i];
                maxIndex = i;
            }
        }
		// 划分左右子树
        TreeNode node = new TreeNode(maxVal);
        node.left = constructMaximumBinaryTreeRec(nums,leftIndex,maxIndex);
        node.right = constructMaximumBinaryTreeRec(nums,maxIndex+1,rightIndex);
        return node;
    }
}