来源：力扣（LeetCode）

描述：

  给你一个无向图（原始图），图中有 n 个节点，编号从 0 到 n - 1 。你决定将图中的每条边 细分 为一条节点链，每条边之间的新节点数各不相同。

  图用由边组成的二维数组 edges 表示，其中 edges[i] = [ui, vi, cnti] 表示原始图中节点 ui 和 vi 之间存在一条边，cnti 是将边 细分 后的新节点总数。注意，cnti == 0 表示边不可细分。

  要 细分 边 [ui, vi] ，需要将其替换为 (cnti + 1) 条新边，和 cnti 个新节点。新节点为 x1, x2, ..., xcnti ，新边为 [ui, x1], [x1, x2], [x2, x3], ..., [xcnti+1, xcnti], [xcnti, vi] 。

  现在得到一个 新的细分图 ，请你计算从节点 0 出发，可以到达多少个节点？如果节点间距离是 maxMoves 或更少，则视为 可以到达 。

给你原始图和 maxMoves ，返回 新的细分图中从节点 0 出发 可到达的节点数 。

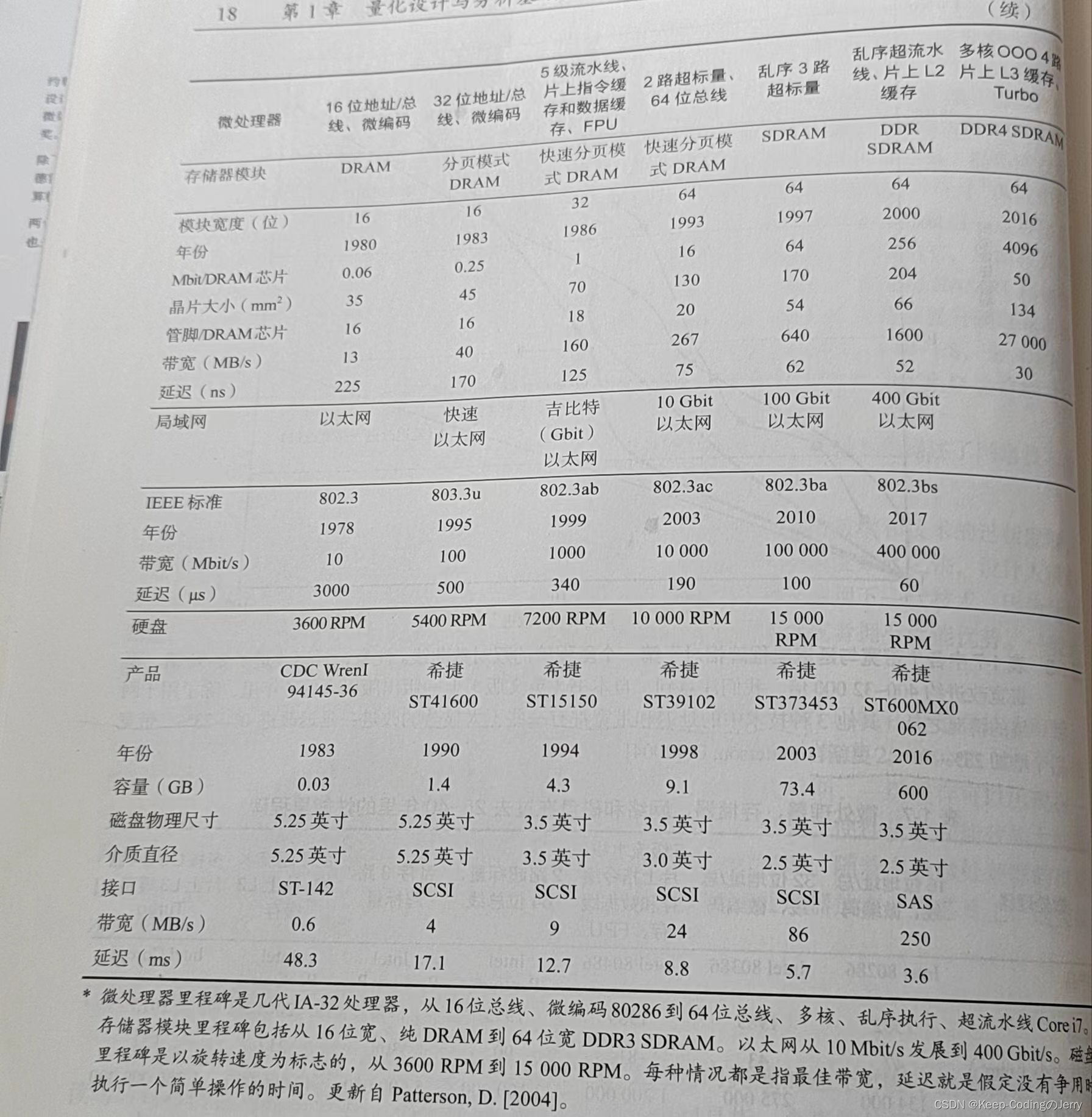
示例 1：

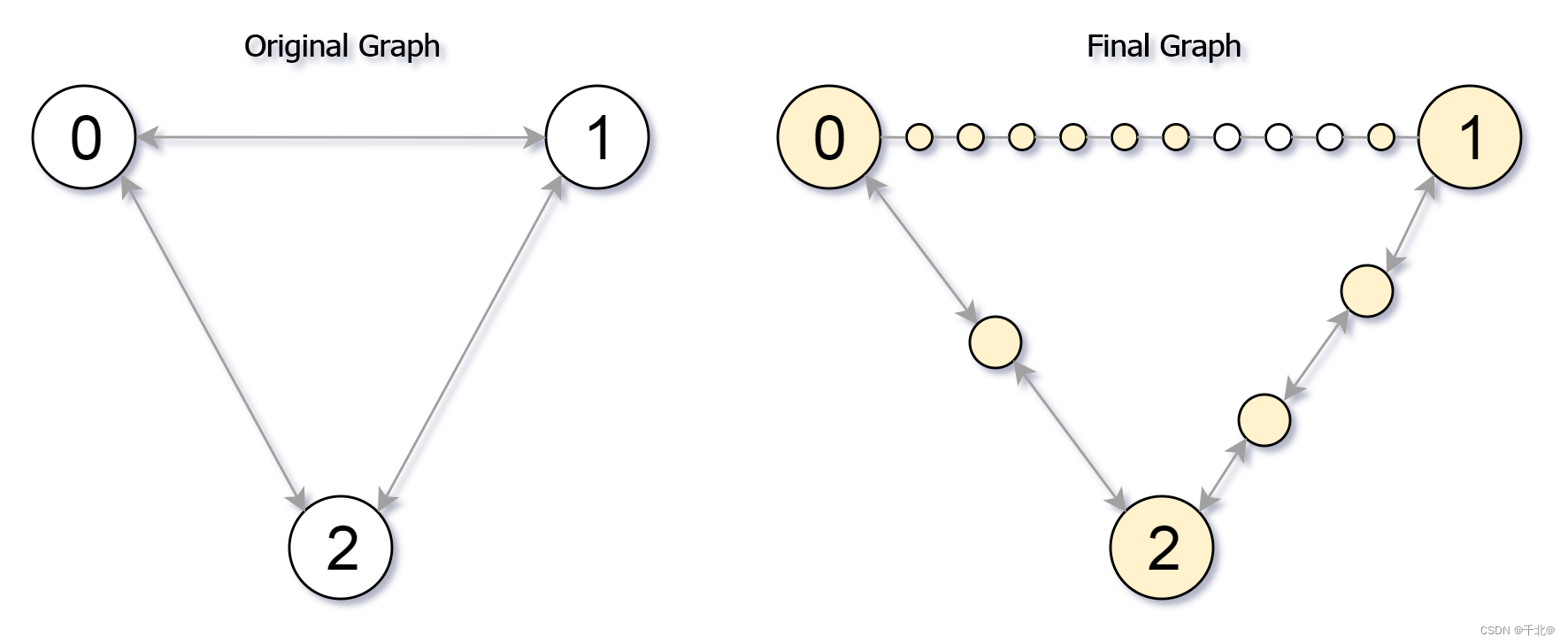
输入：edges = [[0,1,10],[0,2,1],[1,2,2]], maxMoves = 6, n = 3
输出：13
解释：边的细分情况如上图所示。
可以到达的节点已经用黄色标注出来。

示例 2：

输入：edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], maxMoves = 10, n = 4
输出：23

示例 3：

输入：edges = [[1,2,4],[1,4,5],[1,3,1],[2,3,4],[3,4,5]], maxMoves = 17, n = 5
输出：1
解释：节点 0 与图的其余部分没有连通，所以只有节点 0 可以到达。

提示：

• 0 <= edges.length <= min(n * (n - 1) / 2, 10⁴)
• edges[i].length == 3
• 0 <= ui < vi < n
• 图中 不存在平行边
• 0 <= cnti <= 10⁴
• 0 <= maxMoves <= 10⁹
• 1 <= n <= 3000

方法：Dijkstra 算法

思路

  当图中只存在原始节点而不存在细分节点时，此题可以用 Dijkstra 算法解决：将输入的 edges 转换成邻接表 adList，维护一个小顶堆 pq 可以依次计算出图中的起点到各个点最短路径，从而计算出可到达节点。pq 中的元素为节点以及起点到该节点的路径长度，并以路径长度为比较元素。每次取出未访问过的节点中的路径最短的节点，并访问其邻接点，若路径长度仍小于等于 maxMoves 且未访问过，可将其放入 pq，直至 pq 为空或 pq 最短路径大于 maxMoves。

  但当每条边上都加入细分节点后，需要考虑细分节点是否可达。用一个哈希表 used 记录各条边上的细分节点的可达情况，键为二元点对 (u, v) 表示从点 u 到点 v 的边，值为这条边上的可达细分节点数。注意在计算细分节点时，是考虑单向的情况，即会分别计算 used[(u, v)] 和 used[(v,u)]，并且这两个值不一定相等。计算 used 时，是要在访问路径最短的节点 u 的邻接节点 v 时计算。如果邻接节点的路径长度小于等于 maxMoves，说明这条边上的细分节点都可达，否则只有一部分可达，且这部分细分节点是靠近节点 u 的。

  计算总的可达节点时，需要加上细分节点的部分。但每条边上的细分节点可能会被计算过两次，即 used[(u, v) 和 used[(v, u)]，他们分别是是靠近 u 开始计算的和靠近 v 开始计算的，需要对这两部分进行去重。

代码：

class Solution {
public:
    int encode(int u, int v, int n) {
        return u * n + v;
    }

    int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {
        vector<vector<pair<int, int>>> adList(n);
        for (auto &edge : edges) {
            int u = edge[0], v = edge[1], nodes = edge[2];
            adList[u].emplace_back(v, nodes);
            adList[v].emplace_back(u, nodes);
        }

        unordered_map<int, int> used;
        unordered_set<int> visited;
        int reachableNodes = 0;
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        pq.emplace(0, 0);
        while (!pq.empty() && pq.top().first <= maxMoves) {
            auto [step, u] = pq.top();
            pq.pop();
            if (visited.count(u)) {
                continue;
            }
            visited.emplace(u);
            reachableNodes++;
            for (auto [v, nodes] : adList[u]) {
                if (nodes + step + 1 <= maxMoves && !visited.count(v)) {
                    pq.emplace(nodes + step + 1, v);
                }
                used[encode(u, v, n)] = min(nodes, maxMoves - step);
            }
        }

        for (auto &edge : edges) {
            int u = edge[0], v = edge[1], nodes = edge[2];
            reachableNodes += min(nodes, used[encode(u, v, n)] + used[encode(v, u, n)]);
        }
        return reachableNodes;
    }
};

复杂度分析
时间复杂度：O(E×log⁡V)，V 为节点数，即 n，E 为输入 edges 的长度。邻接表 adList 的时间复杂度为 O(E)，Dijkstra 算法的时间复杂度为 O(E×log⁡V)。总的时间复杂度为 O(E×log⁡V)。
空间复杂度：O(V+E)，邻接表 adList 的空间复杂度为 O(E)， pq 的空间复杂度为 O(E)， visited 的空间复杂度为 O(V)，used 的空间复杂度为 O(E)，总的空间复杂度为 O(V+E)。
athor：力扣官方题解