1.129求根节点到叶节点数字之和

参考：代码随想录，129求根节点到叶节点数字之和；力扣题目链接

1.1.题目

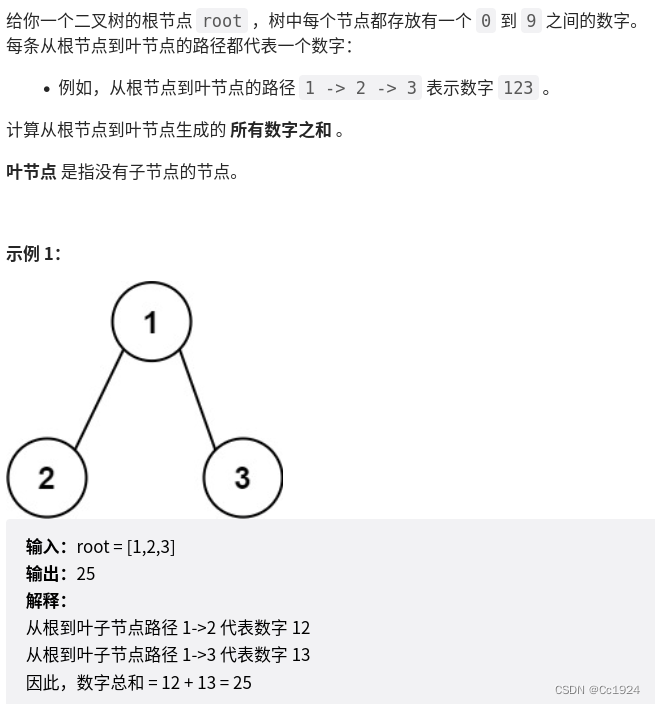
在这里插入图片描述

1.2.解答

这道题和之前做的题目：代码随想录18——二叉树：513找树左下角的值、112路径总和+113路径总和II、106从中序和后序遍历序列构造二叉树+105从前序和中序遍历序列构造二叉树是一样的，就是遍历一条路径，到了叶子节点之后就收集结果，然后进行回溯再遍历其他路径。

很简单，直接给出代码，具体思路去看上面的博客即可。

int result;  // 最终累加的结果
vector<int> path;   // 收集中间路径的值

// 把path中的数字转成int
int vectorToInt(const vector<int>& path)
{
    int sum = 0;
    for(const auto& num : path)
        sum = 10 * sum + num;
    return sum;
}

void traversal(TreeNode* root)
{
    // 2.递归终止条件：到达叶子节点，则开始收集结果
    if(root->left == nullptr && root->right == nullptr)
    {
        result += vectorToInt(path);  // 收集结果
        return;   // 直接返回
    }

    // 3.开始递归
    if(root->left)
    {
        path.push_back(root->left->val);  // 递归之前先把当前的节点的数字加到数组中
        traversal(root->left);   // 递归
        path.pop_back();  // 回溯
    }

    if(root->right)
    {
        path.push_back(root->right->val);
        traversal(root->right);
        path.pop_back();  // 回溯
    }
}

int sumNumbers(TreeNode *root)
{
    if(root == nullptr)
        return 0;
    path.push_back(root->val);  // 先把根节点存到路径中
    traversal(root);  // 然后调用递归
    return result;  // 最后返回结果
}

2.1382将二叉搜索树变平衡

参考：代码随想录，1382将二叉搜索树变平衡；力扣题目链接

2.1.题目

在这里插入图片描述

2.2.解答

这道题目也很简单，就实现先使用中序遍历收集原来的二叉搜索树的节点值，然后重新构造一个平衡的二叉搜索树。之前也做过类似的题目，很简单。

直接给出代码如下：

vector<int> vec;   // 收集原来的二叉树上的节点的结果

// 左中右顺序收集二叉搜索树的所有数字，得到升序的数组
void traversal(TreeNode* root)
{
    if(root == nullptr)
        return;
    traversal(root->left);
    vec.push_back(root->val);
    traversal(root->right);
}

// 传入升序数组和左右边界（左闭右闭），构造平衡二叉搜索树
TreeNode* buildTree(const vector<int>& nums, int left, int right)
{
    if(left > right)
        return nullptr;
    
    int middle = left + (right - left) / 2;
    TreeNode* cur = new TreeNode(nums[middle]);
    cur->left = buildTree(nums, left, middle-1);
    cur->right = buildTree(nums, middle+1, right);

    return cur;
}

TreeNode *balanceBST(TreeNode *root)
{
    traversal(root);   // 先收集结果
    return buildTree(vec, 0, vec.size()-1);  // 然后构造二叉搜索树
}

3.100相同的树

参考：代码随想录，100相同的树；力扣题目链接

3.1.题目

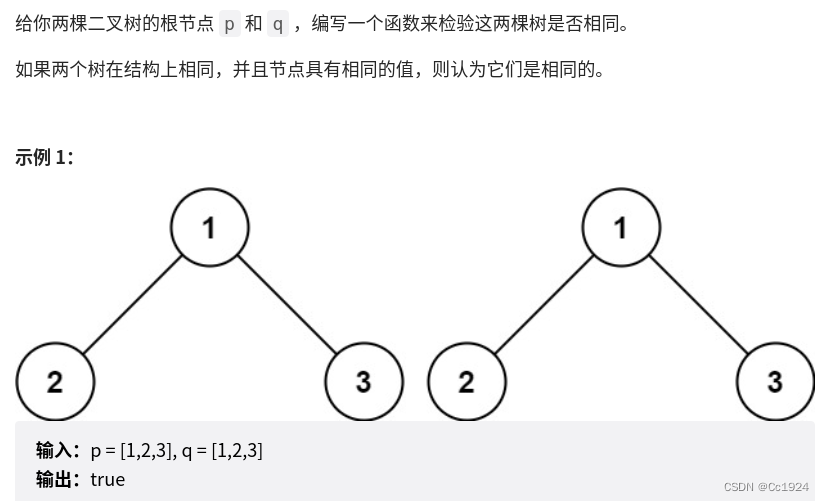
在这里插入图片描述

3.2.解答

这道题目也很简单，和之前做过的一道题目判断一个二叉树是不是对称二叉树是一样的。

直接给出代码如下，很简单：

bool isSameTree(TreeNode *p, TreeNode *q)
{
    // 左右都是空，则相同
    if(p == nullptr && q == nullptr)
        return true;
    else if(p == nullptr && q != nullptr)
        return false;
    else if(p != nullptr && q == nullptr)
        return false;
    else  // 左右都不是空，然后就要比较数值，数值不同则直接false
        if(p->val != q->val)
            return false;

    // 运行到这里，则当前节点不为空，并且数值相同，则需要往下递归
    bool left = isSameTree(p->left, q->left);
    bool right = isSameTree(p->right, q->right);
    return left && right;  // 返回当前节点的结果
}

4.116填充每个节点的下一个右侧节点指针

参考：代码随想录，116填充每个节点的下一个右侧节点指针；力扣题目链接

4.1.题目

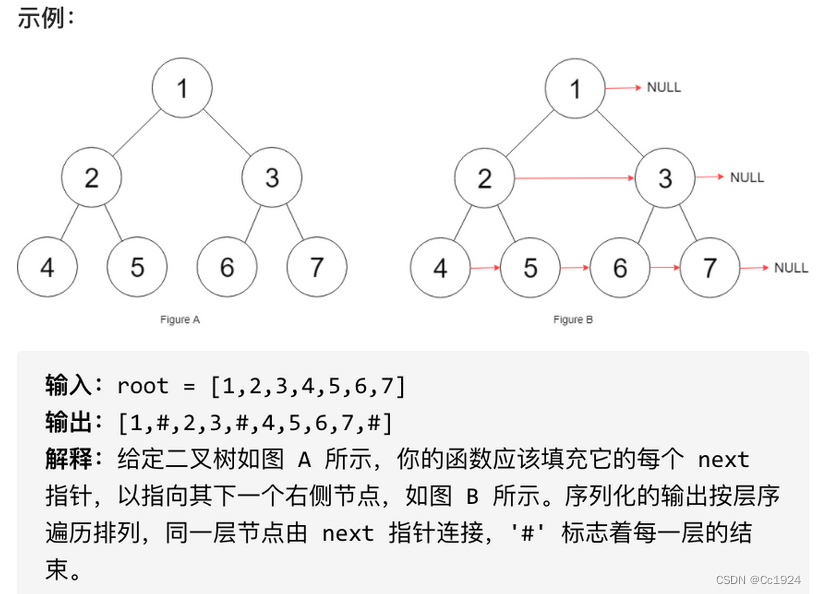
在这里插入图片描述

4.2.解答

注意题目提示内容，：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

基本上就是要求使用递归了，因为迭代的方式一定会用到栈或者队列，一定会使用到额外的空间。

4.2.1.递归解法

一想用递归怎么做呢，虽然层序遍历是最直观的，但是递归的方式确实不好想。

如图，假如当前操作的节点是cur：

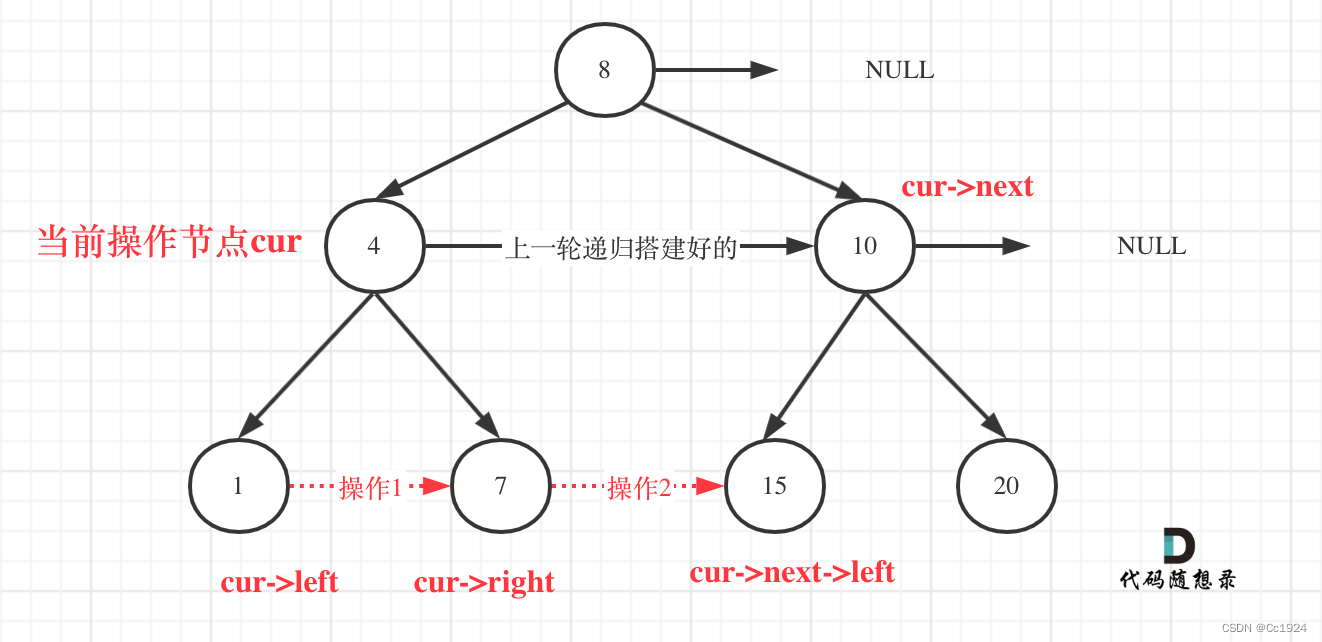
在这里插入图片描述
最关键的点是可以通过上一层递归搭出来的线，进行本次搭线。

图中cur节点为元素4，那么搭线的逻辑代码：（注意注释中操作1和操作2和图中的对应关系）

if (cur->left) cur->left->next = cur->right; // 操作1
if (cur->right) {
    if (cur->next) cur->right->next = cur->next->left; // 操作2
    else cur->right->next = NULL;
}

最后给出如下完整代码：

void traversal(Node* root)
{
    if(root == nullptr)
        return;
    // 中
    if(root->left)   
        root->left->next = root->right;  // 注意完美二叉树，所以左不为空的话，右一定也不为空
    if(root->right)  
    {
        if(root->next)  // 上一层有连接线的话，就可以给本层的连接线提供桥梁
            root->right->next = root->next->left;
        else
            root->right->next = nullptr;
    }

    // 左右
    traversal(root->left);
    traversal(root->right);
}

Node *connect(Node *root)
{
    traversal(root);
    return root;
}

4.2.2.迭代方法

本题使用层序遍历是最为直观的，遍历每一行的时候，如果不是最后一个Node，则指向下一个Node；如果是最后一个Node，则指向nullptr。

代码如下：

Node *connect(Node *root)
{
    queue<Node *> que;
    if (root == nullptr)
        return root;
    que.push(root);

    while (!que.empty())
    {
        int size = que.size(); // 当前要遍历的这一层的节点个数
        // 遍历这一层的所有节点
        for (int i = 0; i < size; i++)
        {
            Node *cur = que.front();
            que.pop();
            if(i < size - 1)
                cur->next = que.front();
            else
                cur->next = nullptr;
            // 把这个节点的子节点（即下一层）加到队列中，为下一次遍历做准备
            if (cur->left != nullptr)
                que.push(cur->left);
            if (cur->right != nullptr)
                que.push(cur->right);
        }
    }

    return root;
}