本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).

There are n + 1 taps located at points [0, 1, ..., n] in the garden.

Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.

Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

Example 1:

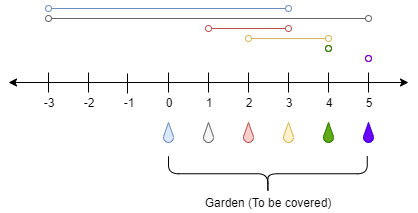
Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]

Example 2:

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.

Constraints:

• 1 <= n <= 104
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

题意：x轴上一座一维花园 [0, n]，长度为 n 。花园中共有 n + 1 个水龙头，分别位于 [0, 1, ..., n] ，整数数组 ranges 中的 ranges[i] 表示 i 处水龙头可以灌溉 [i -  ranges[i], i + ranges[i]] 区域。返回可以灌溉整个花园的最少水龙头数目，如果无法完全灌溉，则返回-1。

---

解法 贪心+桶排（最优）

首先解释示例2为什么要输出-1：因为「整个花园」包含不是整点的位置，即小数位置也要被灌溉到，但输入只能灌溉 $0,1,2,3$ 这 $4$ 个整点。

一般来说，这种覆盖区间类型的题，可以先进行常规排序再求解，但时间复杂度会到 $O(n\log n)$ 。直观来说，第一次选择的区间，自然会想让它的左边界不大于0的同时，右边界尽可能地大，然后第二次选择区间，在其左边界不大于第一次选择的右边界的同时，右边界尽可能地大，依次类推，直至右边界到达n。如果用这种方法，我们就可以按照每一个区间的左边界，对其进行正序排序（不用排序二级排序右边界）。

借用别人的图：

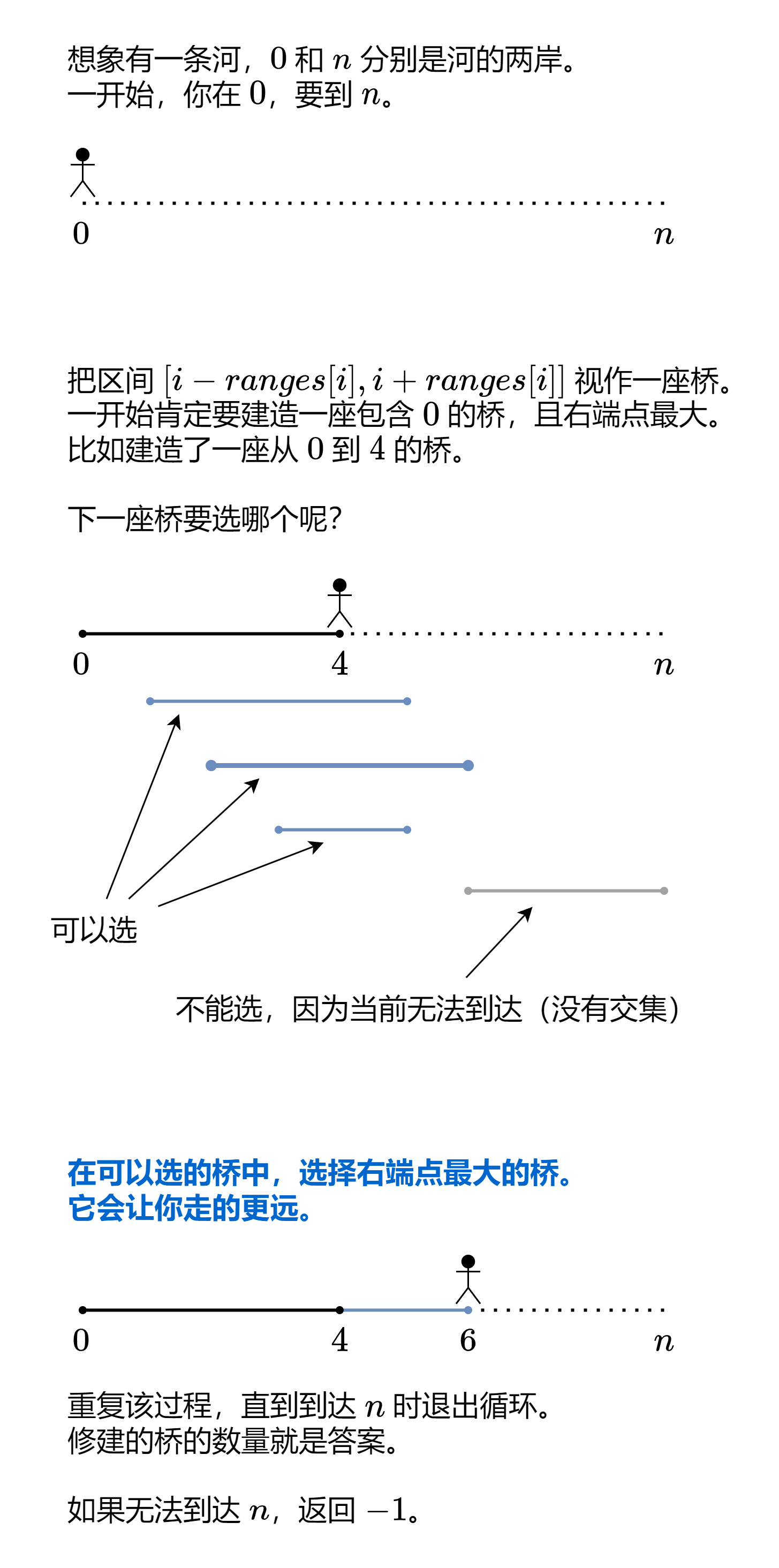
由于这里区间的左边界是整数，可以使用桶排，设置一个 rightMost 数组，对当前的 i 及其半径 ranges[i] ：

• 当 i > ranges[i] 时，对该水龙头能覆盖的最左边界 i - ranges[i] 而言，能覆盖的最右边界一定是 i + ranges[i] ，即 rightMost[i - ranges[i]] = i + ranges[i] 。假如 j < i ，且 j - ranges[j] 能覆盖的最左边界也是 i - ranges[i] ，则 ranges[j] 一定小于 ranges[i] 、且 j + ranges[j] < i + ranges[i] 。
• 当 i <= ranges[i] 时，更新 rightMost[0] 的值为 max(rightMost[0], i + ranges[i] ，即灌溉最左边界小于等于0的水龙头中，灌溉最右边界不一定是 i + ranges[i] ，取最大值。

class Solution {
public:
    int minTaps(int n, vector<int>& ranges) {
        vector<int> rightMost(n + 1);
        for (int i = 0; i <= n; ++i) {
            int r = ranges[i]; // r是半径
            if (i > r) rightMost[i - r] = i + r; // 对于i-r来说,i+r必然是它目前的最大值
            else rightMost[0] = max(rightMost[0], i + r);
        }
        int ans = 0;
        int curRight = 0, nextRight = 0; // 已建造的桥的右端点,下一座桥的右端点的最大值
        for (int i = 0; i < n; ++i) { // 注意这里没有遍历到n,因为它已经是终点了
            nextRight = max(nextRight, rightMost[i]);
            if (i == curRight) { // 到达已被覆盖的灌溉处的右端点 // 到达已建造的桥的右端点 
                if (i == nextRight) return -1; // 无论怎么开水龙头,都无法从i灌溉到i+1 // 无论怎么造桥，都无法从i到i+1
                curRight = nextRight; // 开能到最右处的水龙头 // 造一座桥
                ++ans;
            }
        }
        return ans;
    }
};