模式识别 —— 第一章 贝叶斯决策理论
前言
新的学期开始了,当然是要给不爱吃香菜的月亮记录学习笔记呀~
没多久了,待夏花绚烂之时~人山人海,我们如约而至!
以后清河海风 溶溶月色 共赏之人 就在身侧 mua~
文章目录
- 模式识别 —— 第一章 贝叶斯决策理论
- 前言
- 贝叶斯决策
- 先验概率
- 类条件概率
- 后验概率
- 最大后验概率决策(最小错误率决策)
- 最小风险决策
- 含拒取的最小损失判别规则
- N-P判决
- 判别函数和决策面
- 正态分布下的贝叶斯决策
- 协方差方差矩阵
贝叶斯决策
先验概率
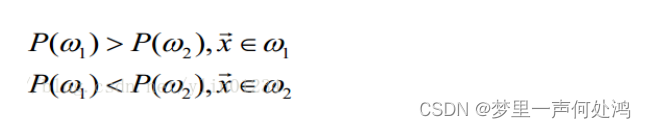
先验概率就是人们根据一些先验知识预先知道的一些概率。比如,南理工男女比例7:3.
类条件概率

就是在先验概率
w
i
w_i
wi的条件下发生
x
x
x事件的概率。
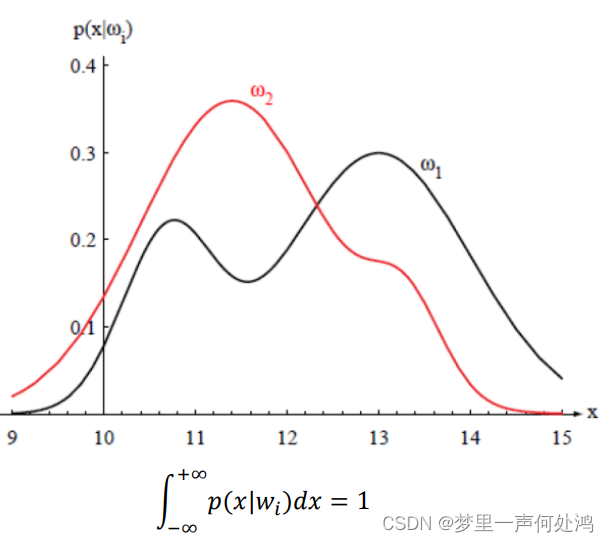
后验概率
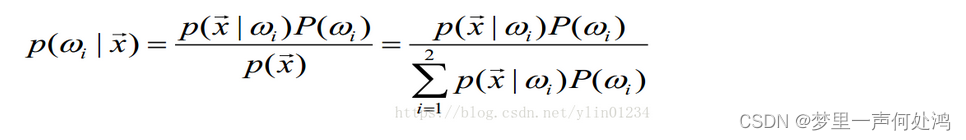
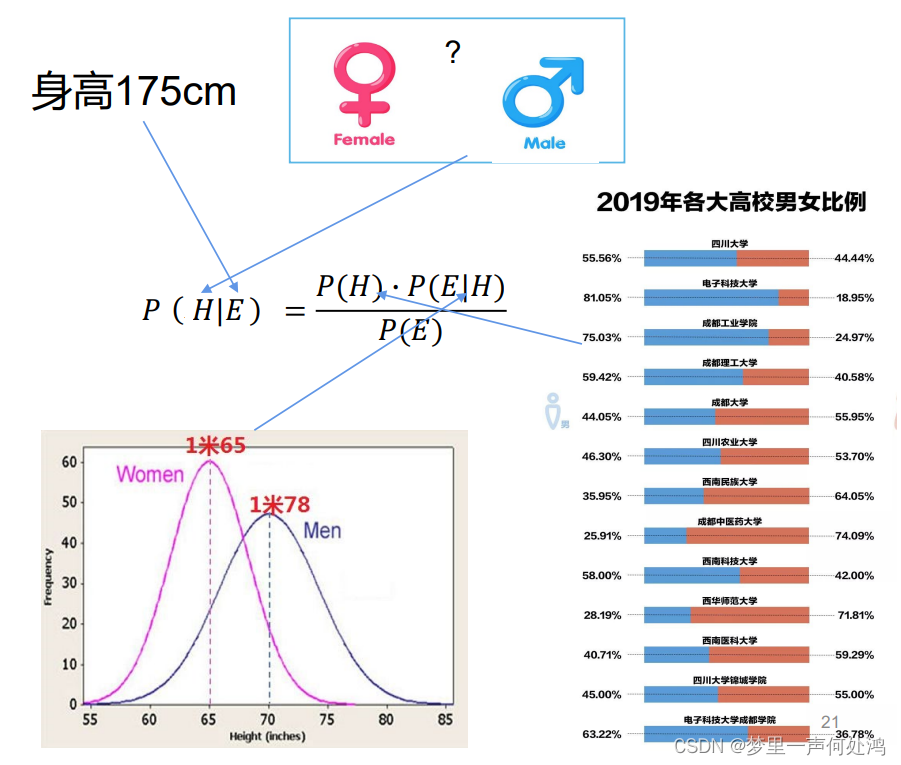
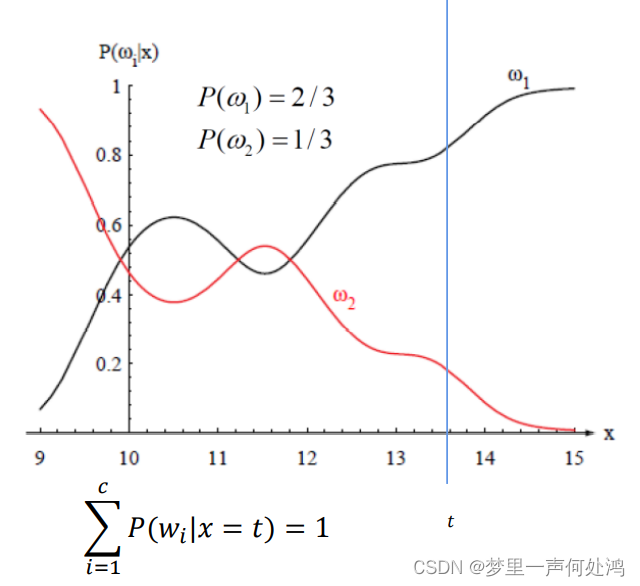
由这张图也可以看出,最大后验概率决策其实就是最小错误决策。
最大后验概率决策(最小错误率决策)
后验概率形式:
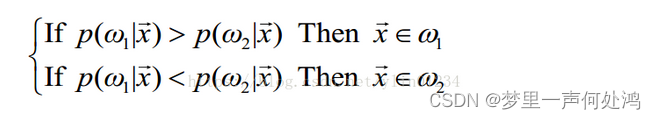
条件概率形式
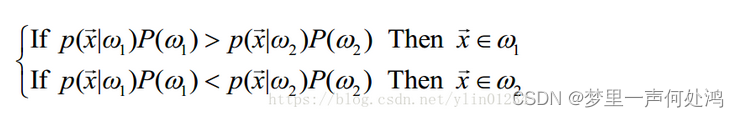
其实就是用贝叶斯公式展开后约去分母
似然比形式
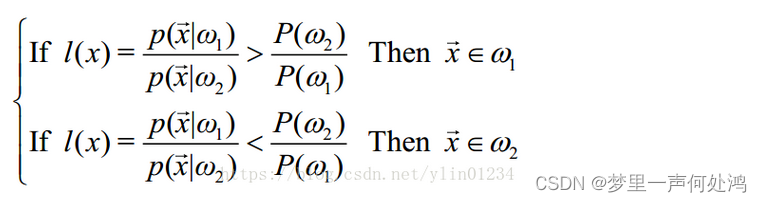 通过上式移项得到。
通过上式移项得到。
对数形式
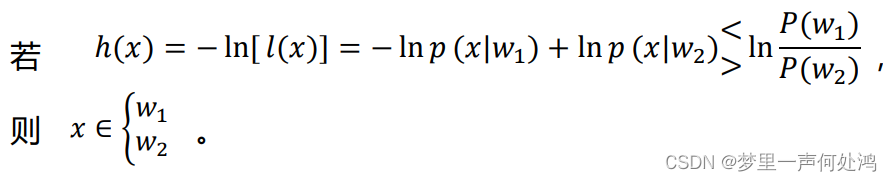
主要是方便求导,也可将之后的累乘化为累加。
最小风险决策
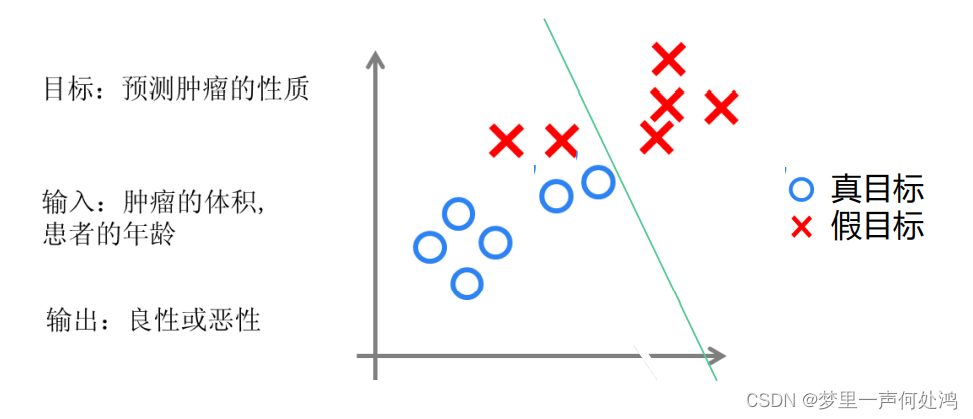
从不同性质的错误会引起不同程度的损失这一考虑出发,我们有时宁肯扩大一些总的错误率,也要使总的损失最小。这就提出了最小损失准则的决策方法。例如,有时2类代价相差很大,比如医疗诊断的场合、工业检测。
为了区分不同错误的代价,我们这里引入了决策代价。

对应的决策代价表如下:

在采取决策
a
j
a_j
aj的条件期望是:
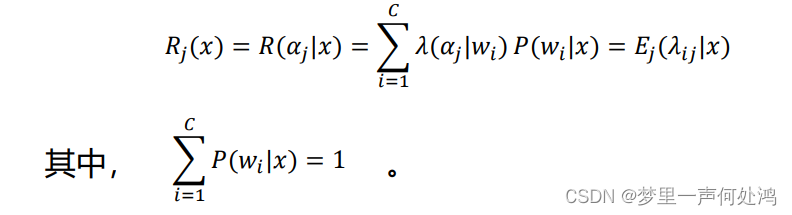
看所有判决对应的期望,选最小的风险判决。
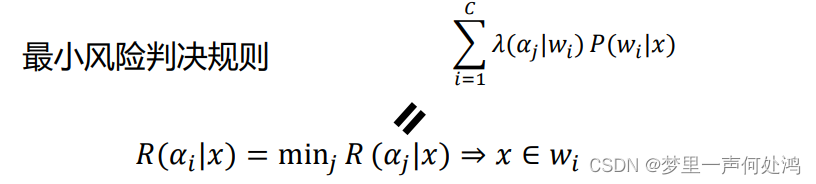
整体流程如下:


最小错误率判决(最大后验概率判决)与最小风险决策的似然比形式一样,只不过在判别阈值上最小风险决策要加上损失代价。
含拒取的最小损失判别规则
例如,人脸识别中有一些未识别的情况,而不是错误的将你识别成另外一个人。那么当后验概率小于多少时采取拒取呢?如下图推导:
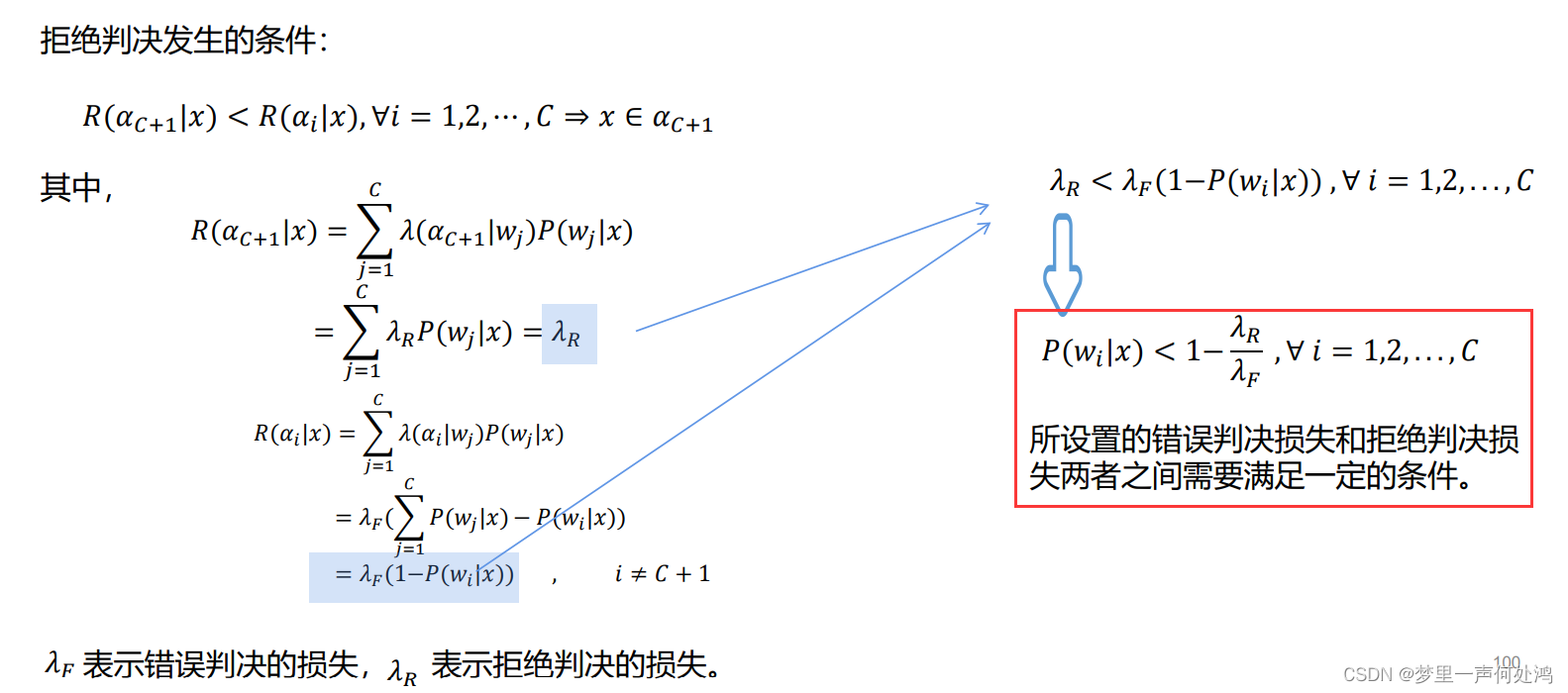
N-P判决
在实际问题中,可能存在某一个错误较另一个错误更为重要。于是我们想在限定一类错误的概率下使得另一类错误的概率最小。

- 例如,在人脸识别中判断错误比未识别要严重许多。所以我们要求判断错误的概率要不超过 1 0 − 6 10^{-6} 10−6(要不超过6位密码的安全级才能投入使用)。在此基础上,我们尽量降低拒取的概率。这里用的是拉格朗日乘子法,不再详解。
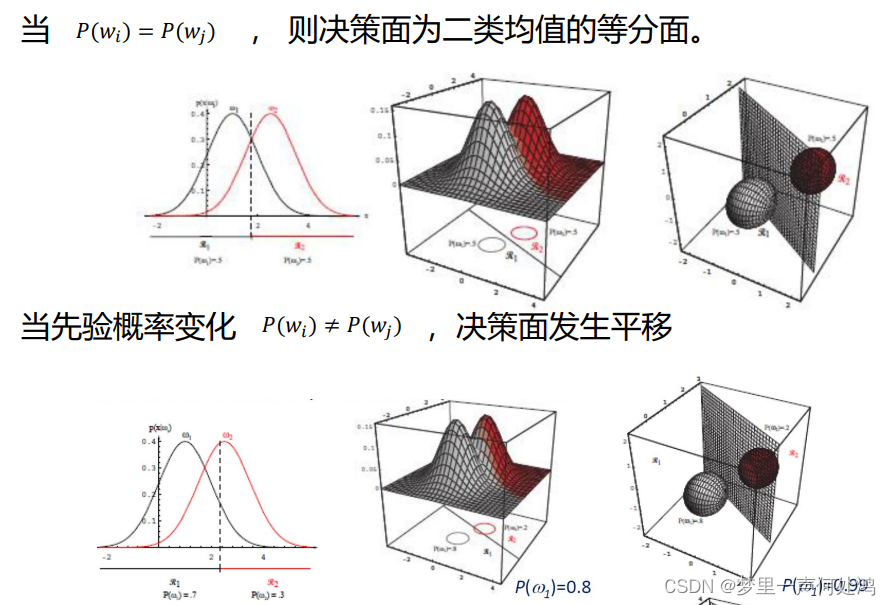
判别函数和决策面
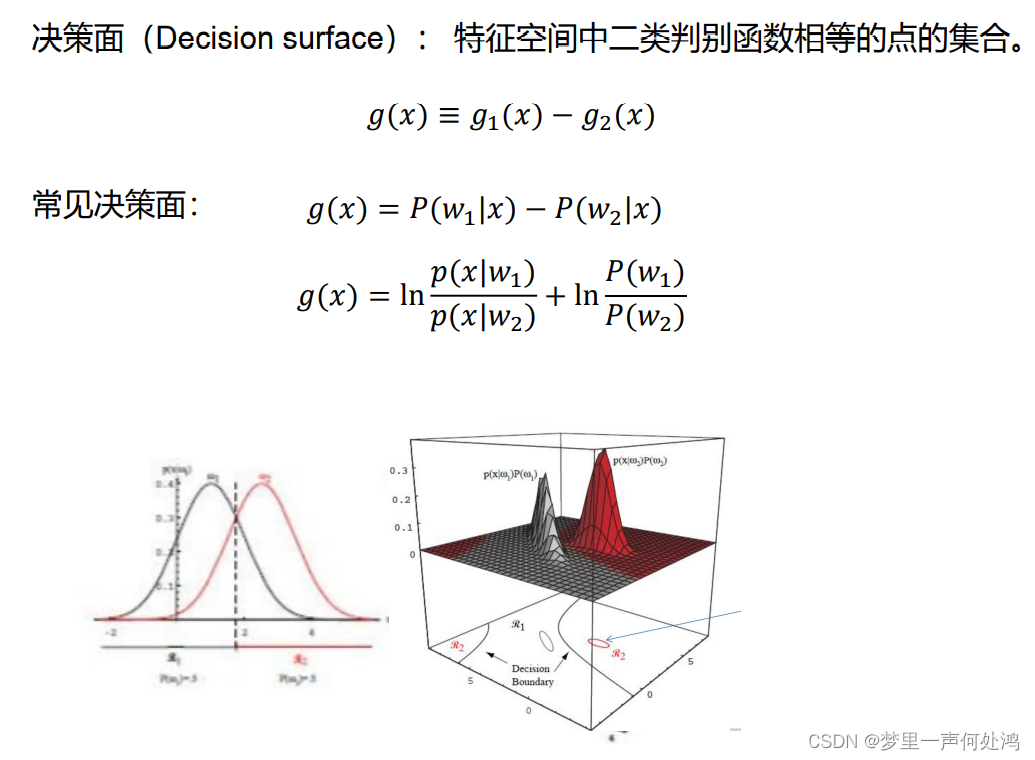
正态分布下的贝叶斯决策
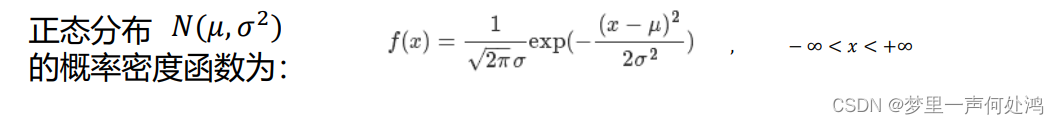
对于二维正态分布有如下公式:
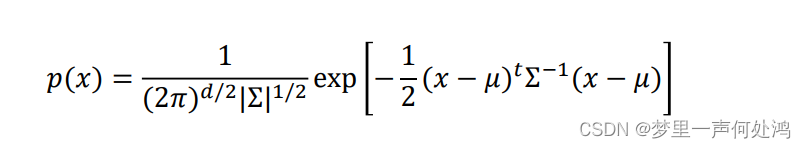
这里的
Σ
\Sigma
Σ是协方差矩阵
协方差方差矩阵
协方差定义
X、Y 是两个随机变量,X、Y 的协方差 cov(X, Y) 定义为:
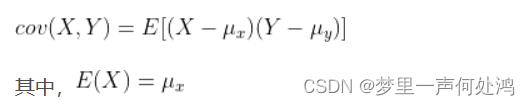
协方差矩阵定义
矩阵中的数据按行排列与按列排列求出的协方差矩阵是不同的,这里默认数据是按行排列。即每一行是一个observation(or sample),那么每一列就是一个随机变量。
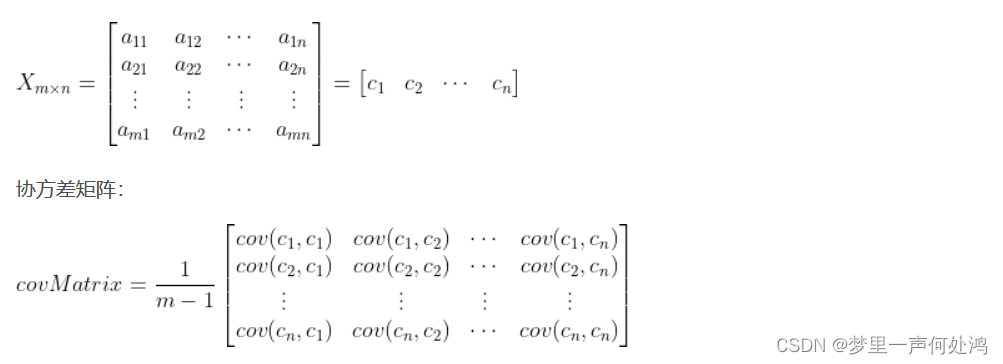
求解协方差矩阵的步骤

协方差代表的意义
正相关
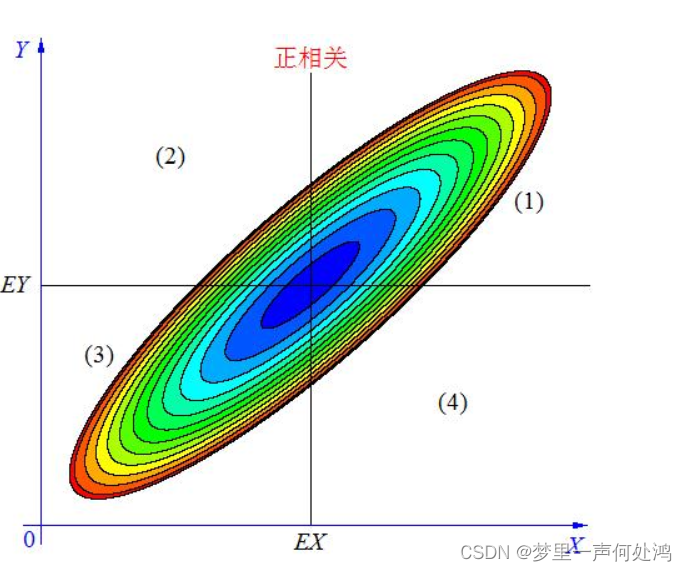
负相关
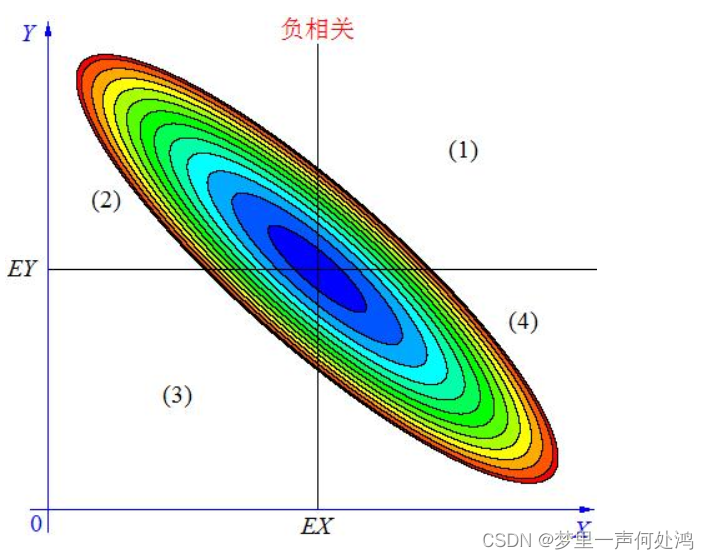
不相关
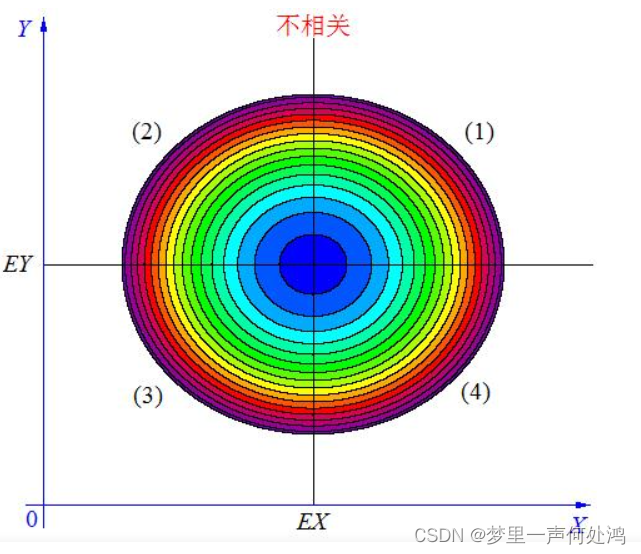
-
当X 与Y 正相关时,它们的分布大部分在区域(1)和(3)中,小部分在区域(2)和(4)中,所以平均来说,有 ( X − E X ) ( Y − E Y ) > 0 (X-EX)(Y-EY)>0 (X−EX)(Y−EY)>0 。
-
当 X与 Y负相关时,它们的分布大部分在区域(2)和(4)中,小部分在区域(1)和(3)中,所以平均来说,有 ( X − E X ) ( Y − E Y ) < 0 (X-EX)(Y-EY)<0 (X−EX)(Y−EY)<0。
-
当 X与 Y不相关时,它们在区域(1)和(3)中的分布,与在区域(2)和(4)中的分布几乎一样多,所以平均来说,有 ( X − E X ) ( Y − E Y ) = 0 (X-EX)(Y-EY)=0 (X−EX)(Y−EY)=0 。
所以,我们可以定义一个表示X, Y 相互关系的数字特征,也就是协方差.
c o v ( X , Y ) = E ( X − E X ) ( Y − E Y ) cov(X, Y) = E(X-EX)(Y-EY) cov(X,Y)=E(X−EX)(Y−EY)
当 c o v ( X , Y ) > 0 cov(X, Y)>0 cov(X,Y)>0时,表明 X与Y 正相关;
当 c o v ( X , Y ) < 0 cov(X, Y)<0 cov(X,Y)<0时,表明X与Y负相关;
当 c o v ( X , Y ) = 0 cov(X, Y)=0 cov(X,Y)=0时,表明X与Y不相关。