这里的内容基本参考于 https://www.jianshu.com/p/51a405bc52ed ,因为写得很好,也没啥补充的,就当做记录一下。
这里先简单解决变形的问题,关于 OpenGL 更多图形矩阵变换,等后面再详细讲。
一. 归一化设备坐标
在OpenGL中,我们要渲染的所有物体都要映射到x轴、y轴、z轴上的[-1, 1]范围内,这个范围内的坐标被称为归一化设备坐标,其独立于屏幕的实际尺寸或者形状。
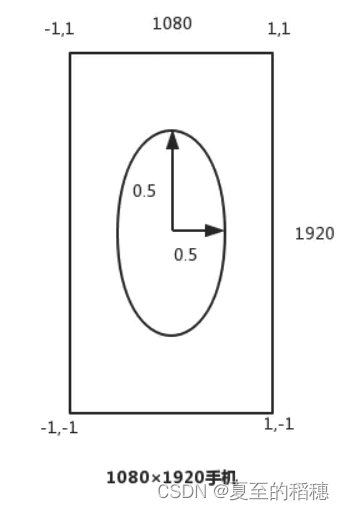
OpenGL 的坐标 它是个正方形的:

而手机屏幕是长方形的,横竖屏的效果都不一样。同样的比例,视觉上是不一样的,比如绘制一个半径为 0.5 的圆,效果却是一个椭圆:
二. 解决方案
解决此问题,可以把一个物品的坐标,通过平移,缩放的方式,塞到到这个归一化坐标里面就可以了。
可以使用 正交投屏 来处理变形的问题,因为正交投影,没有远近距离的关系。
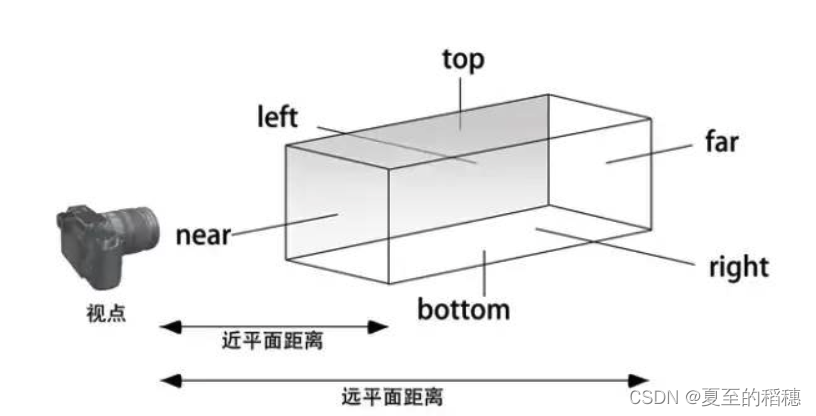
比如一个手机是竖屏,分辨率 1920x1080 ,怎么样把它放到 [-1,1] 里面?
有两个步骤
- 以短边为基准,比如 1080,取值为 [-1,1],那边长边缩放后 n = 长/宽 就是 [-n,n],比如 1920/1080 ≈ 1.78
- 顶点着色器,在设置坐标位置的时候,从 [-n,n] 换算到 [-1,1] 范围内即可。
三. 代码实现
上面的步骤中,第一步比较好实现,在内容变化后,以短边为基准,拿到宽高的比例。
第二步如何实现?
在三维图形学中,一般使用的是4阶矩阵。OpenGL中使用的是列向量,如[xyzw]T,所以与矩阵相乘时,矩阵在前,向量在后。
知道了原理之后,我们代码实现上需要解决以下几个问题:
- 如何获得一个矩阵,可以把坐标范围从[-N,N]换算为[-1,1]的范围内
- 如何将矩阵传递到GLSL中
- 对于问题1,Android提供了Matrix.orthoM这个方法来处理矩阵。
- 对于问题2,与获取顶点索引类似,可以再GLSL中声明一个mat4类型的矩阵变量,获取其索引,再传递值给它
在之前多边形的代码中,修改顶点代码如下,增加一个矩阵变量:
private const val VERTEX_SHADER = """
attribute vec4 a_Position;
mat4:4×4的矩阵
uniform mat4 u_Matrix;
void main()
{
// 矩阵与向量相乘得到最终的位置
gl_Position = u_Matrix * a_Position;
gl_PointSize = 30.0;
}
"""
private const val U_COLOR = "u_Color"
private const val U_MATRIX = "u_Matrix"
//单位矩阵,单位矩阵乘以任何数都等于乘数本身
private val UnitMatrix = floatArrayOf(
1f, 0f, 0f, 0f,
0f, 1f, 0f, 0f,
0f, 0f, 1f, 0f,
0f, 0f, 0f, 1f
)
override fun onSurfaceCreated(gl: GL10?, config: EGLConfig?) {
GLES20.glClearColor(1f, 1f, 1f, 1f)
....
uMatrix = getUniform(U_MATRIX)
}
在 gl 变化时,设置矩阵
override fun onSurfaceChanged(gl: GL10?, width: Int, height: Int) {
GLES20.glViewport(0, 0, width, height)
val aspectRatio = if (width > height) {
width.toFloat() / height
} else {
height.toFloat() / width
}
// 1. 矩阵数组
// 2. 结果矩阵起始的偏移量
// 3. left:x的最小值
// 4. right:x的最大值
// 5. bottom:y的最小值
// 6. top:y的最大值
// 7. near:z的最小值
// 8. far:z的最大值
// 由于是正交矩阵,所以偏移量为0,near 和 far 也不起作用,让他们不相等即可
if (width > height){
Matrix.orthoM(UnitMatrix,0,-aspectRatio,aspectRatio,-1f,1f,0f,1f)
}else{
Matrix.orthoM(UnitMatrix,0,-1f,1f,-aspectRatio,aspectRatio,0f,1f)
}
//更新 matrix 的值,即把 UnitMatrix 值,更新到 uMatrix 这个索引
GLES20.glUniformMatrix4fv(uMatrix,1,false, UnitMatrix,0)
}
参考:
哔哩哔哩 视频:https://www.bilibili.com/video/BV12t4y1c7zd/?spm_id_from=333.337.search-card.all.click
https://www.jianshu.com/p/51a405bc52ed