题目链接

Leetcode.1801 积压订单中的订单总数 Rating ： 1711

题目描述

给你一个二维整数数组 orders，其中每个 orders[i] = [pricei, amounti, orderTypei]表示有 amounti笔类型为 orderTypei、价格为 pricei的订单。

订单类型 orderTypei 可以分为两种：

• 0表示这是一批采购订单 buy
• 1表示这是一批销售订单 sell

注意，orders[i]表示一批共计 amounti笔的独立订单，这些订单的价格和类型相同。对于所有有效的 i，由 orders[i]表示的所有订单提交时间均早于 orders[i+1]表示的所有订单。

存在由未执行订单组成的 积压订单 。积压订单最初是空的。提交订单时，会发生以下情况：

• 如果该订单是一笔采购订单 buy，则可以查看积压订单中价格 最低 的销售订单 sell。如果该销售订单 sell的价格 低于或等于 当前采购订单 buy的价格，则匹配并执行这两笔订单，并将销售订单 sell从积压订单中删除。否则，采购订单 buy将会添加到积压订单中。
• 反之亦然，如果该订单是一笔销售订单 sell，则可以查看积压订单中价格 最高 的采购订单 buy 。如果该采购订单 buy的价格 高于或等于 当前销售订单 sell的价格，则匹配并执行这两笔订单，并将采购订单 buy从积压订单中删除。否则，销售订单 sell将会添加到积压订单中。

输入所有订单后，返回积压订单中的 订单总数 。由于数字可能很大，所以需要返回对 $10^9+7$ 取余的结果。

示例 1：

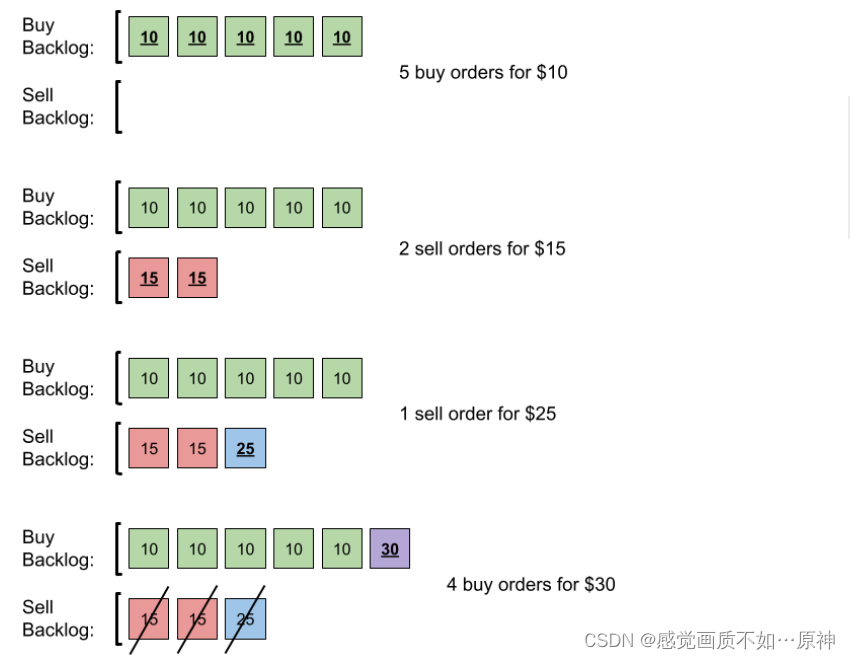
输入：orders = [[10,5,0],[15,2,1],[25,1,1],[30,4,0]]
输出：6
解释：输入订单后会发生下述情况：
提交 5 笔采购订单，价格为 10 。没有销售订单，所以这 5 笔订单添加到积压订单中。
提交 2 笔销售订单，价格为 15 。没有采购订单的价格大于或等于 15 ，所以这 2 笔订单添加到积压订单中。
提交 1 笔销售订单，价格为 25 。没有采购订单的价格大于或等于 25 ，所以这 1 笔订单添加到积压订单中。
提交 4 笔采购订单，价格为 30 。前 2 笔采购订单与价格最低（价格为 15）的 2 笔销售订单匹配，从积压订单中删除这 2 笔销售订单。第 3 笔采购订单与价格最低的 1 笔销售订单匹配，销售订单价格为 25 ，从积压订单中删除这 1
笔销售订单。积压订单中不存在更多销售订单，所以第 4 笔采购订单需要添加到积压订单中。 最终，积压订单中有 5 笔价格为 10
的采购订单，和 1 笔价格为 30 的采购订单。所以积压订单中的订单总数为 6 。

示例 2：

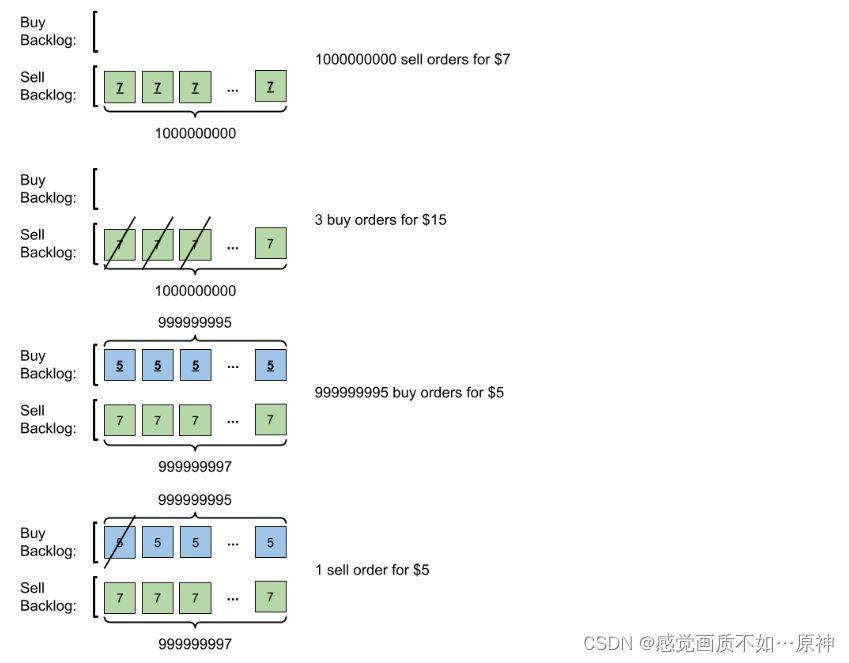
输入：orders = [[7,1000000000,1],[15,3,0],[5,999999995,0],[5,1,1]]
输出：999999984
解释：输入订单后会发生下述情况：
提交 109 笔销售订单，价格为 7 。没有采购订单，所以这 109 笔订单添加到积压订单中。
提交 3 笔采购订单，价格为 15 。这些采购订单与价格最低（价格为 7 ）的 3 笔销售订单匹配，从积压订单中删除这 3 笔销售订单。
提交 999999995 笔采购订单，价格为 5 。销售订单的最低价为 7 ，所以这 999999995 笔订单添加到积压订单中。
提交 1 笔销售订单，价格为 5 。这笔销售订单与价格最高（价格为 5 ）的 1 笔采购订单匹配，从积压订单中删除这 1 笔采购订单。 最终，积压订单中有 (1000000000-3) 笔价格为 7 的销售订单，和 (999999995-1) 笔价格为 5
的采购订单。所以积压订单中的订单总数为 1999999991 ，等于 999999984 % (10^9 + 7) 。

提示：

• $1<=orders.length<=10^5$
• $orders[i].length==3$
• $1<=pricei,amounti<=10^9$
• orderTypei为 0或 1

分析：

我们用两个 堆 来模拟这个过程。堆里面存的是 (price,amount)这样的二元组。

对于 buy订单，用一个 大顶堆 来存储，因为每次要选择最大的 buy订单。

对于 sell订单，用一个 小顶堆 来存储，因为每次要选择最小的 sell订单。

直接模拟这个过程即可。

时间复杂度：$O(nlogn)$

代码：

const int MOD = 1e9+7;
using PII = pair<int,int>;
class Solution {
public:
    int getNumberOfBacklogOrders(vector<vector<int>>& orders) {
        priority_queue<PII,vector<PII>,greater<PII>> sell;
        priority_queue<PII> buy;
         
        for(auto o:orders){
            int price = o[0] , amount = o[1] , type = o[2];
            //buy
            if(type == 0){
                while(!sell.empty() && sell.top().first <= price){
                    if(amount == 0) break;
                    auto [p,cnt] = sell.top();
                    sell.pop();
                    if(cnt <= amount) amount -= cnt;
                    else{
                        cnt -= amount;
                        amount = 0;
                        sell.push({p,cnt});
                    }
                }
                if(amount > 0) buy.push({price,amount}); 
            }
            //sell
            else{
                while(!buy.empty() && buy.top().first >= price){
                    if(amount == 0) break;
                    auto [p,cnt] = buy.top();
                    buy.pop();
                    if(cnt <= amount) amount -= cnt;
                    else{
                        cnt -= amount;
                        amount = 0;
                        buy.push({p,cnt});
                    }
                }
                if(amount > 0) sell.push({price,amount});
            }

        }

        int ans = 0;
        while(!sell.empty()){
            auto[_,cnt] = sell.top();
            ans = (ans + cnt) % MOD;
            sell.pop();
        }

        while(!buy.empty()){
            auto[_,cnt] = buy.top();
            ans = (ans + cnt) % MOD;
            buy.pop();
        } 

        
        return ans;       
    }
};