【HDU No. 2874】 城市之间的联系 Connections between cities

杭电OJ 题目地址

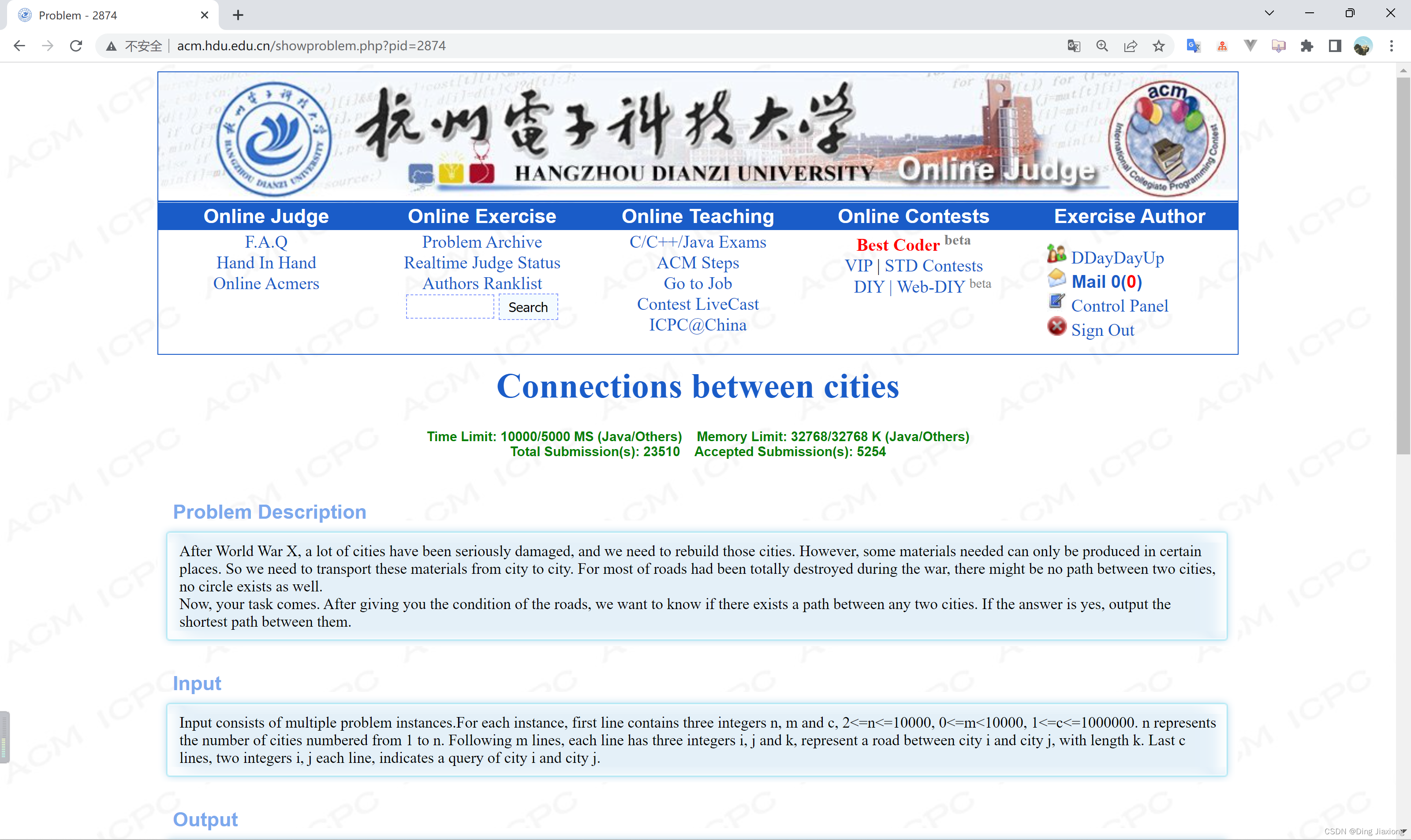
【题意】

由于大部分道路在战争期间已被完全摧毁，所以两个城市之间可能没有路径，也没有环。

已知道路状况，想知道任意两个城市之间是否存在路径。若答案是肯定的，则输出它们之间的最短距离。

【输入输出】

输入：

输入包含多个测试用例。每个用例的第1行都包含3个整数n、m、c （2≤n ≤10000，0≤m <10000，1≤c ≤1000000）。n 表示城市数，编号为1～n 。接下来的m 行，每行都包含3个整数i、j 和k，表示城市i 和城市j 之间的道路，长度为k 。

最后c 行，每行都包含i、j 两个整数，表示查询城市i 和城市j 之间的最短距离。

输出：

对每个查询，若两个城市之间没有路径，则输出“Not connected”，否则输出它们之间的最短距离。

【样例】

【思路分析】

这道题的两点之间无环，且有可能不连通，有可能不是一棵树，而是由多棵树组成的森林。

因此需要判断是否在同一棵树中，若不在同一棵树中，则输出“Not connected”，否则可以使用求解最近公共祖先的Tarjan算法求解。

【算法设计】

① 根据输入的数据，采用链式前向星存储图。

② 采用Tarjan算法离线处理所有查询。因为本题的操作对象可能有多棵树，因此需要注意两个问题：

• [1] 修改Tarjan算法，引入一个root参数，用来判断待查询的两个节点是否在同一棵树中；
• [2] 对未访问过的节点再次执行Tarjan算法。

③ 将每个查询中两个节点之间的距离都存储在答案数组中。

【算法实现】

#include<cstdio>
#include<cstring>

using namespace std;

const int maxn=1e4+10;
const int maxq=1e6+10;

struct Node{//边结构体 
	int to;//邻接点 
	int w;//边权 
	int next;//下一条边的下标 
}e[maxn<<1];

int ehead[maxn],dis[maxn],fa[maxn],ecnt,vis[maxn];

struct Query{//边结构体 
	int to;
	int id;//查询的编号 
	int next;
}qe[maxq<<1];

int qhead[maxn],ans[maxq],qcnt;
int n,m,c;
 
void init(){
	ecnt=qcnt=0;
	memset(ehead,-1,sizeof(ehead));
	memset(qhead,-1,sizeof(qhead));
	memset(vis,-1,sizeof(vis));
}
 
void add1(int u,int v,int w){
	e[ecnt].to=v;
	e[ecnt].w=w;
	e[ecnt].next=ehead[u];
	ehead[u]=ecnt++;
}
 
void add2(int u,int v,int id){
	qe[qcnt].id=id;
	qe[qcnt].to=v;
	qe[qcnt].next=qhead[u];
	qhead[u]=qcnt++;
}
 
int Find(int x){
	if(x!=fa[x])
		fa[x]=Find(fa[x]);
	return fa[x];
}
 
void LCA(int u,int deep,int root){
	fa[u]=u;
	dis[u]=deep;
	vis[u]=root;
	for(int i=ehead[u];~i;i=e[i].next){
		int v=e[i].to;
		if(vis[v]==-1){
			LCA(v,deep+e[i].w,root);
			fa[v]=u;
		}
	}
	for(int i=qhead[u];~i;i=qe[i].next){
		int v=qe[i].to;
		if(vis[v]==root)
			ans[qe[i].id]=dis[v]+dis[u]-2*dis[Find(v)];
	}
}
 
 
int main(){
	
	while(~scanf("%d%d%d",&n,&m,&c)){
		int u,v,w;
		init();
		while(m--){
			scanf("%d%d%d",&u,&v,&w);
			add1(u,v,w);
			add1(v,u,w);	
		}
		for(int i=0;i<c;i++){
			scanf("%d%d",&u,&v);
			ans[i]=-1;
			add2(u,v,i);
			add2(v,u,i);
		}
		for(int i=1;i<=n;i++){
			if(vis[i]==-1)
				LCA(i,0,i);
		}
		for(int i=0;i<c;i++){
			if(ans[i]==-1) printf("Not connected\n");
			else printf("%d\n",ans[i]);
		}
	}
	
	return 0;
}