摘要

剑指 Offer 30. 包含min函数的栈

一、栈解析

package Stock;

import java.util.Stack;

/**
 * @Classname JZ30min函数栈
 * @Description TODO
 * @Date 2023/2/24 18:59
 * @Created by xjl
 */
public class JZ30min函数栈 {

    /**
     * @description 最小栈的含义是每次从栈中获取的数据都是最小
      * @param: null
     * @date: 2023/2/24 19:00
     * @return:
     * @author: xjl
    */
    class MinStack {
        Stack<Integer> stack;

        /** initialize your data structure here. */
        public MinStack() {
            stack = new Stack<>();
        }
        /**
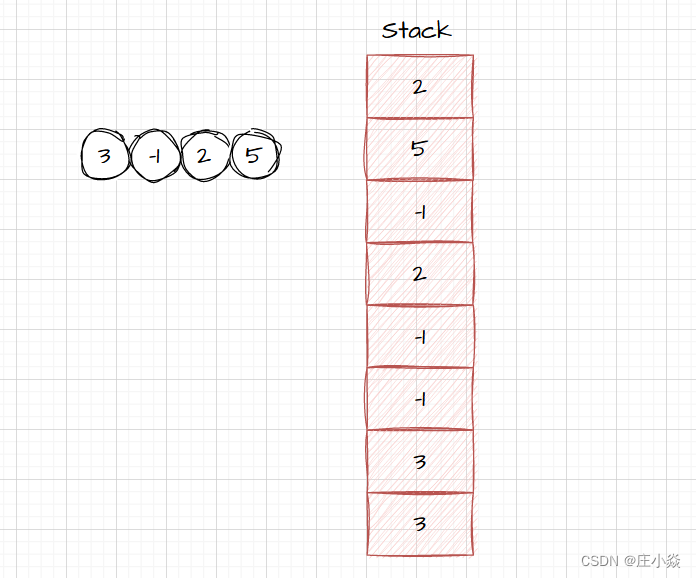
         * @description 每次都是push两个数据当前数据和当前最小的数据
          * @param: x
         * @date: 2023/2/24 19:01
         * @return: void
         * @author: xjl
        */
        public void push(int x) {
            if (stack.isEmpty()) {
                stack.add(x);
                stack.add(x);
            } else {
                int val=stack.peek();
                if (val > x) {
                    stack.add(x);
                    stack.add(x);
                } else {
                    stack.add(x);
                    stack.add(val);
                }
            }
        }
        /**
         * @description 每次都是弹出两个数据
          * @param:
         * @date: 2023/2/24 19:02
         * @return: void
         * @author: xjl
        */
        public void pop() {
            stack.pop();
            stack.pop();
        }

        /**
         * @description 获取顶部的元素，就是获取第二个元素
          * @param:
         * @date: 2023/2/24 19:02
         * @return: int
         * @author: xjl
        */
        public int top() {
            int min=stack.pop();
            int val=stack.pop();
            stack.push(val);
            stack.add(min);
            return val;
        }

        /**
         * @description 每次都是的获取最顶部的元素 
          * @param: 
         * @date: 2023/2/24 19:03
         * @return: int
         * @author: xjl
        */
        public int min() {
            return stack.peek();
        }
    }
}

复杂度分析

时间复杂度：对于题目中的所有操作，时间复杂度均为O(1)。因为栈的插入、删除与读取操作都是 O(1)，我们定义的每个操作最多调用栈操作两次。
空间复杂度：O(2n)，其中n为总操作数。最坏情况下，我们会连续插入n个元素，此时两个栈占用的空间为O(n)。

二、使用两个栈来实现

对于栈来说，如果一个元素a在入栈时，栈里有其它的元素b, c, d，那么无论这个栈在之后经历了什么操作，只要a在栈中，b, c, d 就一定在栈中，因为在 a 被弹出之前，b, c, d 不会被弹出。

因此，在操作过程中的任意一个时刻，只要栈顶的元素是 a，那么我们就可以确定栈里面现在的元素一定是 a, b, c, d。

那么，我们可以在每个元素a入栈时把当前栈的最小值m存储起来。在这之后无论何时，如果栈顶元素是 a，我们就可以直接返回存储的最小值m。

按照上面的思路，我们只需要设计一个数据结构，使得每个元素 a 与其相应的最小值 m 时刻保持对应。因此我们使用一个辅助栈，与元素栈同步插入与删除，用于存储与每个元素对应的最小值。

当一个元素要入栈时，我们取当前辅助栈的栈顶存储的最小值，与当前元素比较得出最小值，将这个最小值插入辅助栈中；
当一个元素要出栈时，我们把辅助栈的栈顶元素也一并弹出；
在任意一个时刻，栈内元素的最小值就存储在辅助栈的栈顶元素中。

class MinStack {
    Deque<Integer> Stack;
    Deque<Integer> minStack;

    public MinStack() {
        Stack = new LinkedList<Integer>();
        minStack = new LinkedList<Integer>();
        minStack.push(Integer.MAX_VALUE);
    }
    
    public void push(int x) {
        Stack.push(x);
        minStack.push(Math.min(minStack.peek(), x));
    }
    
    public void pop() {
        Stack.pop();
        minStack.pop();
    }
    
    public int top() {
        return Stack.peek();
    }
    
    public int min() {
        return minStack.peek();
    }
}

复杂度分析