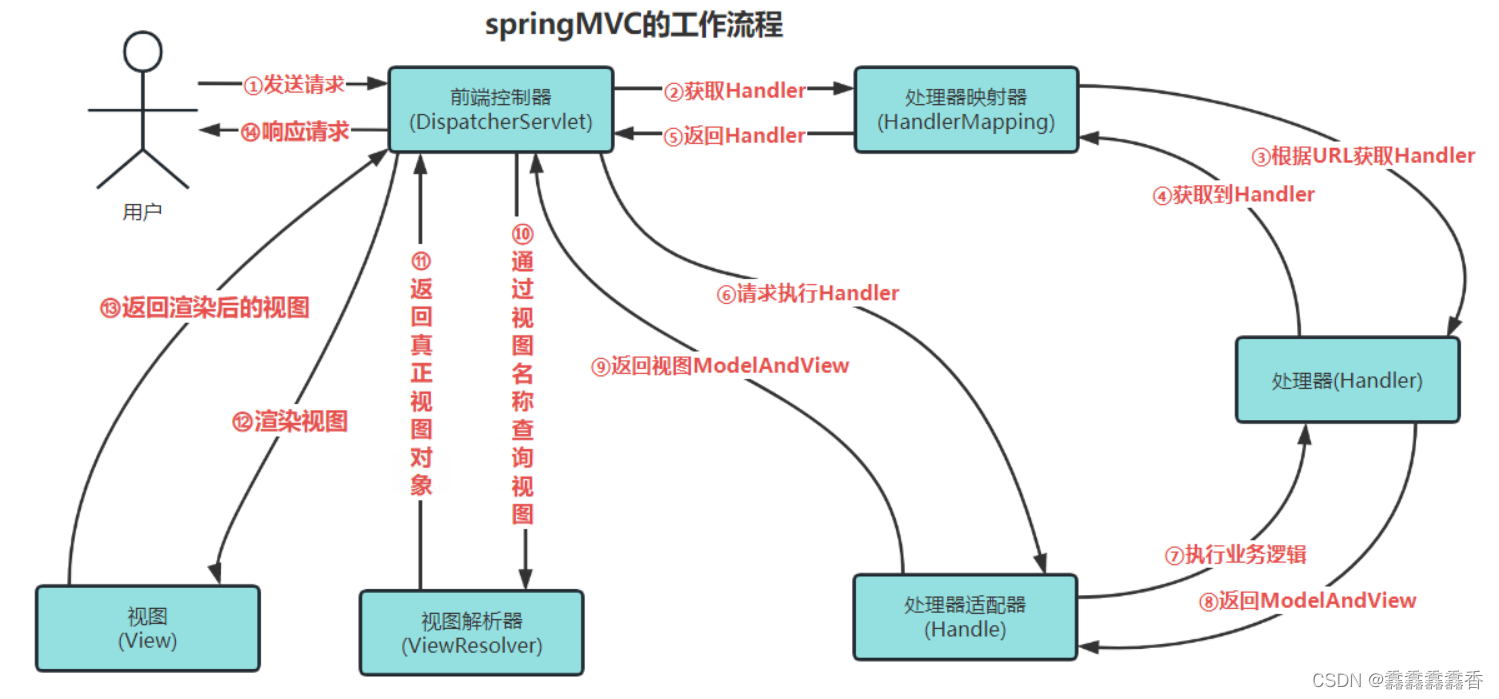
Julia 提供了一套高效、可移植的标准数学函数。

---

数值比较

下表列出了用于数值比较的函数：

函数	测试是否满足如下性质
isequal(x, y)	x 与 y 值与类型是否完全相同
isfinite(x)	x 是否是有限大的数字
isinf(x)	x 是否是（正/负）无穷大
isnan(x)	x 是否是 NaN

isequal 认为 NaN 之间是相等的：

实例

julia> isequal(NaN, NaN)
true

julia> isequal([1 NaN], [1 NaN])
true

julia> isequal(NaN, NaN32)
true

isequal 也能用来区分带符号的零：

实例

julia> -0.0 == 0.0
true

julia> isequal(-0.0, 0.0)
false

其他函数实例：

实例

julia> isfinite(5)
true

julia> isfinite(NaN32)
false

---

舍入函数

下表列出了 Julia 支持的舍入函数：

函数	描述	返回类型
round(x)	x 舍到最接近的整数	typeof(x)
round(T, x)	x 舍到最接近的整数	T
floor(x)	x 向 -Inf 舍入	typeof(x)
floor(T, x)	x 向 -Inf 舍入	T
ceil(x)	x 向 +Inf 方向取整	typeof(x)
ceil(T, x)	x 向 +Inf 方向取整	T
trunc(x)	x 向 0 取整	typeof(x)
trunc(T, x)	x 向 0 取整	T

实例

julia> round(3.8)
4.0
julia> round(Int, 3.8)
4
julia> floor(3.8)
3.0
julia> floor(Int, 3.8)
3
julia> ceil(3.8)
4.0
julia> ceil(Int, 3.8)
4
julia> trunc(3.8)
3.0
julia> trunc(Int, 3.8)
3

---

除法函数

下表列出了 Julia 支持的除法函数：

函数	描述
div(x,y), x÷y	截断除法，无论任何类型相除的结果都会省略小数部分，剩下整数部分，商向零近似。
fld(x,y)	向下取整除法；商向 -Inf 近似
cld(x,y)	向上取整除法；商向 +Inf 近似
rem(x,y)	取余；满足 x == div(x,y)*y + rem(x,y)；符号与 x 一致
mod(x,y)	取模；满足 x == fld(x,y)*y + mod(x,y)；符号与 y 一致
mod1(x,y)	偏移 1 的 mod；若 y>0，则返回 r∈(0,y]，若 y<0，则 r∈[y,0) 且满足 mod(r, y) == mod(x, y)
mod2pi(x)	对 2pi 取模；0 <= mod2pi(x) < 2pi
divrem(x,y)	返回 (div(x,y),rem(x,y))
fldmod(x,y)	返回 (fld(x,y),mod(x,y))
gcd(x,y...)	x, y,... 的最大公约数
lcm(x,y...)	x, y,... 的最小公倍数

实例

julia> div(11, 4)
2

julia> div(7, 4)
1

julia> fld(11, 4)
2

julia> fld(-5,3)
-2

julia> fld(7.5,3.3)
2.0

julia> cld(7.5,3.3)
3.0

julia> mod(5, 0:2)
2

julia> mod(3, 0:2)
0

julia> mod(8.9,2)
0.9000000000000004

julia> rem(8,4)
0

julia> rem(9,4)
1

julia> mod2pi(7*pi/5)
4.39822971502571

julia> divrem(8,3)
(2, 2)

julia> fldmod(12,4)
(3, 0)

julia> fldmod(13,4)
(3, 1)

julia> mod1(5,4)
1

julia> gcd(6,0)
6

julia> gcd(1//3,2//3)
1//3

julia> lcm(1//3,2//3)
2//3

---

符号和绝对值函数

下表列出了 Julia 支持的符号和绝对值函数：

函数	描述
abs(x)	x 的模
abs2(x)	x 的模的平方
sign(x)	表示 x 的符号，返回 -1，0，或 +1
signbit(x)	表示符号位是 true 或 false
copysign(x,y)	返回一个数，其值等于 x 的模，符号与 y 一致
flipsign(x,y)	返回一个数，其值等于 x 的模，符号与 x*y 一致

实例

julia> abs(-7)
7

julia> abs(5+3im)
5.830951894845301

julia> abs2(-7)
49

julia> abs2(5+3im)
34

julia> copysign(5,-10)
-5

julia> copysign(-5,10)
5

julia> sign(5)
1

julia> sign(-5)
-1

julia> signbit(-5)
true

julia> signbit(5)
false

julia> flipsign(5,10)
5

julia> flipsign(5,-10)
-5

---

符号和绝对值函数

下表列出了 Julia 支持的符号和绝对值函数：

函数	描述
sqrt(x), √x	x 的平方根
cbrt(x), ∛x	x 的立方根
hypot(x,y)	当直角边的长度为 x 和 y时，直角三角形斜边的长度
exp(x)	自然指数函数在 x 处的值
expm1(x)	当 x 接近 0 时的 exp(x)-1 的精确值
ldexp(x,n)	x*2^n 的高效算法，n 为整数
log(x)	x 的自然对数
log(b,x)	以 b 为底 x 的对数
log2(x)	以 2 为底 x 的对数
log10(x)	以 10 为底 x 的对数
log1p(x)	当 x接近 0 时的 log(1+x) 的精确值
exponent(x)	x 的二进制指数
significand(x)	浮点数 x 的二进制有效数（也就是尾数）

实例

julia> sqrt(49)
7.0

julia> sqrt(-49)
ERROR: DomainError with -49.0:
sqrt will only return a complex result if called with a complex argument. Try sqrt(Complex(x)).
Stacktrace:
 [1] throw_complex_domainerror(::Symbol, ::Float64) at .\math.jl:33
 [2] sqrt at .\math.jl:573 [inlined]
 [3] sqrt(::Int64) at .\math.jl:599
 [4] top-level scope at REPL[43]:1
 
julia> cbrt(8)
2.0

julia> cbrt(-8)
-2.0

julia> a = Int64(5)^10;

julia> hypot(a, a)
1.3810679320049757e7

julia> exp(5.0)
148.4131591025766

julia> expm1(10)
22025.465794806718

julia> expm1(1.0)
1.718281828459045

julia> ldexp(4.0, 2)
16.0

julia> log(5,2)
0.43067655807339306

julia> log(4,2)
0.5

julia> log(4)
1.3862943611198906

julia> log2(4)
2.0

julia> log10(4)
0.6020599913279624

julia> log1p(4)
1.6094379124341003

julia> log1p(-2)
ERROR: DomainError with -2.0:
log1p will only return a complex result if called with a complex argument. Try log1p(Complex(x)).
Stacktrace:
 [1] throw_complex_domainerror(::Symbol, ::Float64) at .\math.jl:33
 [2] log1p(::Float64) at .\special\log.jl:356
 [3] log1p(::Int64) at .\special\log.jl:395
 [4] top-level scope at REPL[65]:1
julia> exponent(6.8)
2

julia> significand(15.2)/10.2
0.18627450980392157

julia> significand(15.2)*8
15.2

---

三角和双曲函数

Julia 也提供了所有标准的三角和双曲函数：

sin    cos    tan    cot    sec    csc
sinh   cosh   tanh   coth   sech   csch
asin   acos   atan   acot   asec   acsc
asinh  acosh  atanh  acoth  asech  acsch
sinc   cosc

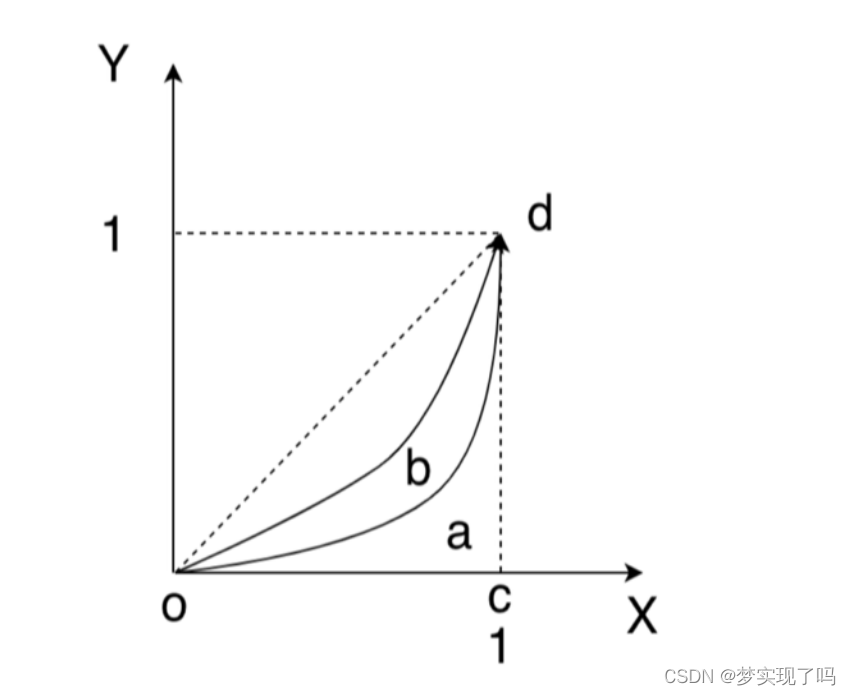
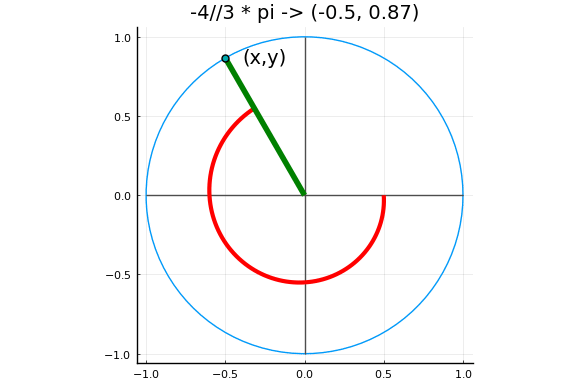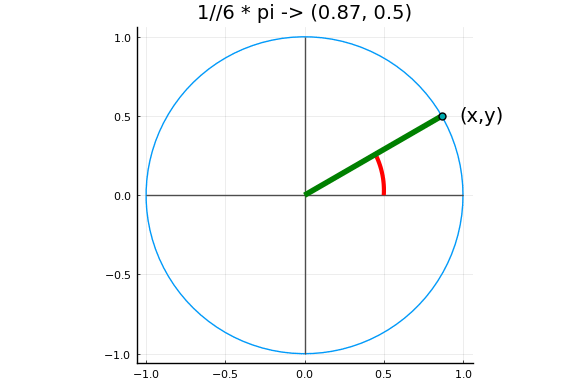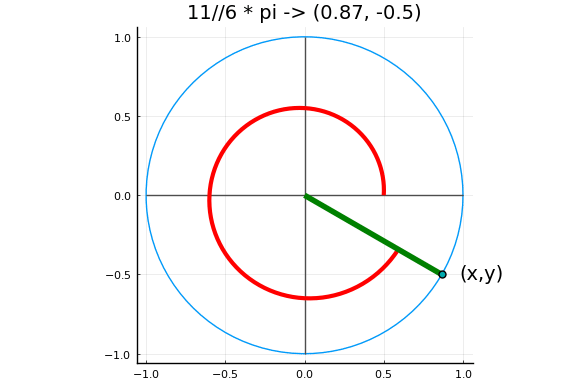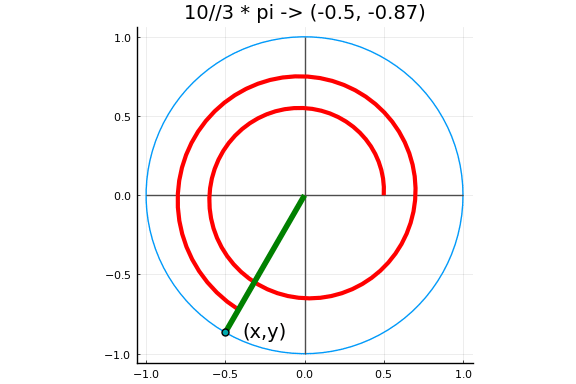
下图中以弧度为单位的角度对应于单位圆上的一个点，其坐标定义了角度的正弦和余弦。

实例

julia> pi
π = 3.1415926535897...

julia> sin(0)
0.0

julia> sin(pi/6)
0.49999999999999994

julia> sin(pi/4)
0.7071067811865475

julia> cos(0)
1.0

julia> cos(pi/6)
0.8660254037844387

julia> cos(pi/3)
0.5000000000000001

以上提供的函数都是单参数函数，不过 atan 也可以接收两个参数 来表示传统的 atan2 函数。

atan(y)
atan(y, x)

分别计算 y 或 y/x 的反正切。

实例

julia> theta = 3pi/4
2.356194490192345

julia> x,y = (cos(theta), sin(theta))
(-0.7071067811865475, 0.7071067811865476)

julia> atan(y/x)
-0.7853981633974484

julia> atan(y, x)
2.356194490192345

另外，sinpi(x) 和 cospi(x) 分别用来对 sin(pi*x) 和 cos(pi*x) 进行更精确的计算。

要计算角度而非弧度的三角函数，以 d 做后缀。 比如，sind(x) 计算 x 的 sine 值，其中 x 是一个角度值。 下面是角度变量的三角函数完整列表：

sind   cosd   tand   cotd   secd   cscd
asind  acosd  atand  acotd  asecd  acscd

实例

julia> cos(56)
0.853220107722584

julia> cosd(56)
0.5591929034707468