深度学习笔记：误差反向传播（2）

反向传播上一章内容可见http://t.csdn.cn/SHW3m

1 激活函数的反向传播

ReLU

ReLU函数在x > 0的时候返回x，在X <= 0的时候返回0。对该函数求导可得∂y/∂x 在x > 0时为1，在x <= 0时为0
在这里插入图片描述

class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0

        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout

        return dx

在该程序中，mask为一个boolean数组。self.mask = (x <= 0)将x中所有小于0的元素位置对应为True，将x大于0的元素位置对应False

Sigmoid
在这里插入图片描述
sigmoid函数求导结果为(1 + exp(-x)) ^ -2 * exp(-x),这一结果可以进一步简化为y(1 - y)

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx

Affine

Affine层即为矩阵乘法。作用是将输入值乘以权重再加上偏置
在这里插入图片描述
反向传播输出矩阵形状要和输入矩阵形状一致，如X形状为（N,2），∂L/∂X 的形状也要为（N,2）。通过这点我们可以推出图中的反向传播计算公式。如要计算∂L/∂X，我们要将反向传播的输入(N,3)乘以W的同时确保输出形状为（N,2）。要实现这一点，我们可以将（N,3）* (3, 2)得到（N,2）,对应过来即为∂L/∂Y x WT

WT为转置矩阵，其作用是将矩阵横纵颠倒
在这里插入图片描述

对于偏置量，由于在正向传播中将X * W结果的每一维都加上了偏置。如对[[1, 1, 1], [2, 2, 2], [3, 3, 3]]加上偏置[1, 2, 3]的结果为[[2, 3, 4], [3, 4, 5], [4, 5, 6]]。在加法反向传播中，导数结果∂L/∂Y，这里需要将∂L/∂Y关于第0维加和结果作为∂L/∂B。在例子中即为[6, 6, 6]

class Affine:
    def __init__(self, W, b):
        self.W =W
        self.b = b
        
        self.x = None
        self.original_x_shape = None
        # 权重和偏置参数的导数
        self.dW = None
        self.db = None

    def forward(self, x):
        # 对应张量
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x

        out = np.dot(self.x, self.W) + self.b

        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        
        dx = dx.reshape(*self.original_x_shape)  # 还原输入数据的形状（对应张量）
        return dx

softmax-with-loss

在分类问题的输出层，我们一般使用softmax函数。这里我们将softmax和cross-entropy层相连直接得到损失函数，因此被称为softmax-with-loss层。该层计算图如下：
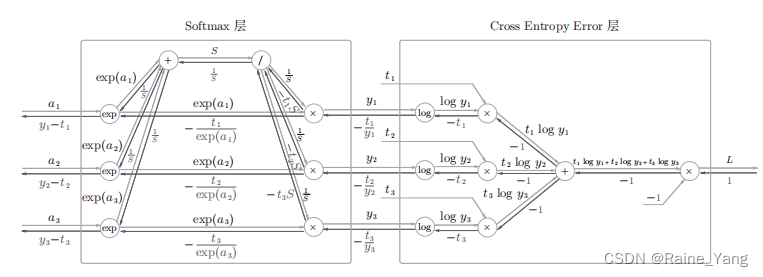
在这里插入图片描述
这里由计算图一步步推得导数结果过程过于复杂。这里我们直接给出反向传播结果为y - t，即为预测值和标签值的差值。

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None # softmax的输出
        self.t = None # 监督数据

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size
        
        return dx

利用误差反向传播搭建的完整神经网络

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict


class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
        # 初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) 
        self.params['b2'] = np.zeros(output_size)

        # 生成层
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])

        self.lastLayer = SoftmaxWithLoss()
        
    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
        
        return x
        
    # x:输入数据, t:监督数据
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)
        
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
        
    # x:输入数据, t:监督数据
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        
        return grads
        
    def gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.lastLayer.backward(dout)
        
        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 设定
        grads = {}
        grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grads

    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
        # 初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) 
        self.params['b2'] = np.zeros(output_size)

        # 生成层
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])

        self.lastLayer = SoftmaxWithLoss()

创建网络，使用随机正态初始化权重和偏置。创建了一个OrderedDict来保存各层。OrderedDict可以保存加入字典的元素顺序

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
        
        return x

逐层正向传播得到输出

    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)

利用sofmax with loss函数计算损失函数

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)
        
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

将网络输出和标签值比较得到预测准确率

    def gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.lastLayer.backward(dout)
        
        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 设定
        grads = {}
        grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grads

使用反向传播发计算梯度。创建layers将各层保存为列表，再将列表翻转得到反向传播的函数顺序。对输出进行反向传播即可得到各层的梯度

梯度确认

数值微分计算梯度是很低效的方法，但是其实现简单，一般不会出错。因此，我们一般利用数值微分的结果对反向传播的结果进行验算，如果验算误差很小，我们可以确定反向传播的方法结果正确。

# coding: utf-8
import sys, os
sys.path.append('D:\AI learning source code')  # 为了导入父目录的文件而进行的设定
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

x_batch = x_train[:3]
t_batch = t_train[:3]

grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backprop = network.gradient(x_batch, t_batch)

for key in grad_numerical.keys():
    diff = np.average( np.abs(grad_backprop[key] - grad_numerical[key]) )
    print(key + ":" + str(diff))

这里我们引入mnist数据集进行测试，结果如下：

W1:4.0712457921539956e-10
b1:2.5670347708844996e-09
W2:5.31776417291195e-09
b2:1.4023633097548504e-07

可以看到两种方法得到的梯度基本一致，反向传播程序正确

利用反向传播发对mnist手写数字集进行分类

# coding: utf-8
import sys, os
sys.path.append('D:\AI learning source code')

import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 梯度
    #grad = network.numerical_gradient(x_batch, t_batch)
    grad = network.gradient(x_batch, t_batch)
    
    # 更新
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print(train_acc, test_acc)

程序和上一章程序（http://t.csdn.cn/tDD17）完全相同，只是方法由数值微分改为反向传播，故不做详解

测试结果

0.11295 0.1126
0.9041 0.9066
0.92065 0.9222
0.9335333333333333 0.935
0.9434166666666667 0.9433
0.9489333333333333 0.9461
0.9547833333333333 0.9521
0.9597666666666667 0.956
0.9631666666666666 0.9579
0.9662666666666667 0.9584
0.9684666666666667 0.9631
0.97145 0.9656
0.9720833333333333 0.9655
0.9738666666666667 0.9659
0.9752833333333333 0.9691
0.9768833333333333 0.9681
0.9780666666666666 0.9679