归并排序算法基于分而治之的概念,具体来说就是遍历一棵树,归并的过程是一个后序执行的动作。 由于我们知道每个子部分在合并后都是有序的,我们可以利用这个特性来解决一些问题。
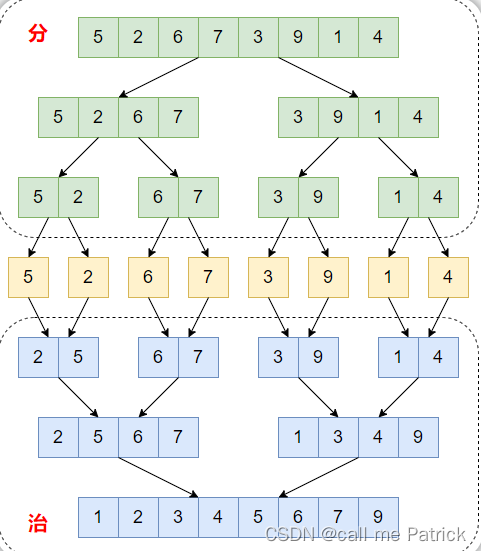
上图可视化了merge sort algorithm的过程,我们很容易看出树的深度是log(N)。 基本上我们必须在合并中对序列进行排序,时间复杂度是 O(N)。 所以这个算法的时间复杂度总共是Nlog(N)。
根据上图的思路,我们可以很容易的编写出下面这个程序。
class Solution
{
public:
vector<int> sortArray(vector<int> &nums)
{
int len = nums.size();
if (len < 2) return;
int mid = len >> 1;
vector<int> leftArray(nums.begin(), nums.begin() + mid);
vector<int> rightArray(nums.begin() + mid, nums.end());
sort(leftArray);
sort(rightArray);
mergeArray(nums, leftArray, rightArray);
return nums;
}
void mergeArray(vector<int> &nums, vector<int> &leftArray, vector<int> &right)
{
int leftSize = leftArray.size(), rightSize = rightArray.size();
int cur = 0, cur1 = 0, cur2 = 0;
while (cur1 < leftSize && cur2 < rightSize)
{
if (leftArray[cur1] <= rightArray[cur2])
nums[cur++] = leftArray[cur1++];
else
nums[cur++] = rightArray[cur2++];
}
while (cur1 < leftSize)
nums[cur++] = leftArray[cur1++];
while (cur2 < rightSize)
nums[cur++] = rightArray[cur2++];
}
};
关于它的应用,我们总是试图找到一个问题是否可以应用合并后子部件有序的特性。 以下是应用“合并排序算法”的一些问题。
315. 计算右侧小于当前元素的个数
假设 i 指向左边的第一个元素,j 和 mid+1 指向右边的第一个元素。 当我们合并的时候,如果 temp[i] 小于 temp[j] ,我们可以知道有 j-mid-1 个元素小于 temp[i] ,因为数组是单调递增的。

所以可以在合并的过程添加一些小小代码,其他的地方不变。
class Solution {
public:
vector<pair<int, int>> temp;
vector<int> count;
vector<int> countSmaller(vector<int>& nums) {
int n = nums.size();
vector<pair<int, int>> num_index;
for (int i = 0; i < n; i++)
num_index.push_back(pair<int, int>(nums[i], i));
temp = vector<pair<int, int>>(n);
count = vector<int>(n, 0);
merge_sort(num_index, 0, n-1);
return count;
}
void merge_sort(vector<pair<int, int>>& num_index, int l, int r){
if (l >= r) return;
int mid = l + (r - l) / 2;
merge_sort(num_index, l, mid);
merge_sort(num_index, mid+1, r);
merge(num_index, l, mid, r);
}
void merge(vector<pair<int, int>>& num_index, int l, int mid, int r){
int i = l, j = mid + 1;
int k = l;
while (i <= mid && j <= r){
if (num_index[i].first <= num_index[j].first){
count[num_index[i].second] += j - mid - 1;
temp[k++] = num_index[i++];
}
else temp[k++] = num_index[j++];
}
while (i <= mid) {
count[num_index[i].second] += j - mid - 1;
temp[k++] = num_index[i++];
}
while (j <= r) temp[k++] = num_index[j++];
for (i = l; i <= r; i++)
num_index[i] = temp[i];
}
};
或者可以在后序位置操作一点点东西。
493. 翻转对
这个问题和上一个一样,只是有点不同。 我们假设下面有有序的左孩子和右孩子。 下一步是合并,但在此之前,我们可以计算左右之间的数字,betValue。 假设左边的数字是 leftValue,右边的数字是 rightValue。 可以递归计算最终结果。
class Solution
{
public:
vector<int> tmp;
int mergeSort(vector<int> &nums, int left, int right)
{
if (left >= right)
return 0;
int mid = left + ((right - left) >> 1);
int retLeft = mergeSort(nums, left, mid);
int retRight = mergeSort(nums, mid + 1, right);
int cur1 = left, cur2 = mid + 1;
int ret = 0;
while (cur1 <= mid)
{
while (cur2 <= right && nums[cur1] / 2.0 > nums[cur2])
cur2++;
ret += cur2 - mid - 1;
cur1++;
}
merge(nums, left, mid, right);
return ret + retLeft + retRight;
}
void merge(vector<int> &nums, int left, int mid, int right)
{
int cur1 = left, cur2 = mid + 1, cur = left;
while (cur1 <= mid && cur2 <= right)
{
if (nums[cur1] <= nums[cur2])
tmp[cur++] = nums[cur1++];
else
tmp[cur++] = nums[cur2++];
}
while (cur1 <= mid)
tmp[cur++] = nums[cur1++];
while (cur2 <= right)
tmp[cur++] = nums[cur2++];
for (int i = left; i <= right; i++)
nums[i] = tmp[i];
}
int reversePairs(vector<int> &nums)
{
int len = nums.size();
tmp = vector<int>(len, 0);
return mergeSort(nums, 0, len - 1);
}
};
那么,如何获得betValue呢? 只需在后序空间添加一些代码。 我们可以得到右边第一个大于 nums[i] / 2.0 的元素。
327. 区间和的个数
是一样的,但是这里需要用到前缀和,理解为什么可以使用merge sort来解决这个问题。
class Solution
{
public:
vector<long> tmp;
int countRangeSum(vector<int> &nums, int lower, int upper)
{
int len = nums.size();
vector<long> preSum({0});
for (int i = 0; i < len; i++)
preSum.emplace_back(preSum[i] + nums[i]);
tmp = vector<long>(preSum.size(), 0);
return mergeSort(preSum, 0, preSum.size() - 1, lower, upper);
}
int mergeSort(vector<long> &nums, int left, int right, int lower, int upper)
{
if (left >= right)
return 0;
int mid = left + ((right - left) >> 1);
int retLeft = mergeSort(nums, left, mid, lower, upper);
int retRight = mergeSort(nums, mid + 1, right, lower, upper);
int cur1 = mid + 1, cur2 = mid + 1;
int ret = 0;
for (int i = left; i <= mid; i++)
{
while (cur1 <= right && nums[cur1] - nums[i] < lower)
cur1++;
while (cur2 <= right && nums[cur2] - nums[i] <= upper)
cur2++;
ret += cur2 - cur1;
}
merge(nums, left, mid, right);
return ret + retLeft + retRight;
}
void merge(vector<long> &nums, int left, int mid, int right)
{
int cur1 = left, cur2 = mid + 1, cur = left;
while (cur1 <= mid && cur2 <= right)
{
if (nums[cur1] <= nums[cur2])
tmp[cur++] = nums[cur1++];
else
tmp[cur++] = nums[cur2++];
}
while (cur1 <= mid)
tmp[cur++] = nums[cur1++];
while (cur2 <= right)
tmp[cur++] = nums[cur2++];
for (int i = left; i <= right; i++)
nums[i] = tmp[i];
}
};