🚀write in front🚀
📜所属专栏:初阶数据结构
🛰️博客主页:睿睿的博客主页
🛰️代码仓库:🎉VS2022_C语言仓库
🎡您的点赞、关注、收藏、评论,是对我最大的激励和支持!!!
关注我,关注我,关注我,你们将会看到更多的优质内容!!

文章目录
- 前言:
- 一.空间复杂度
- 栗子1:
- 栗子2:
- 栗子3:
- 栗子4:
- 二.常见复杂度对比
- 总结:
前言:
上一篇博客我们讲解了时间复杂度的相关知识,那么时间有复杂度,可以有复杂度吗?下面我们就来了解一下空间复杂度的相关知识!
一.空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间(变量个数)来确定。
常数个变量的复杂度:O(n)
栗子1:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
空间复杂度为O(1)
因为调用了常数个常数个额外空间。
栗子2:
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if (n == 0)
return NULL;
long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}
空间复杂度为O(n)
动态开辟了n+1个空间
栗子3:
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if (N == 0)
return 1;
return Fac(N - 1) * N;
}
空间复杂度为O(n)
递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。
栗子4:
// 计算斐波那契递归Fib的空间复杂度?
long long Fib(size_t N)
{
if (N < 3)
return 1;
return Fib(N - 1) + Fib(N - 2);
}
空间复杂度为O(N)
很多小伙伴可能会以为空间复杂度为O(2^N),但是实则不是。我们先来看看下面的图:

递归是有先后顺序,并不是同一时间内同时递归的,所以递归会按先后顺序依次递归,顺序就像如图所示的1 2 3 4 5 6……这样递归。所以开辟的空间最多为N个,随后返回空间。所以空间复杂度为O(N)。
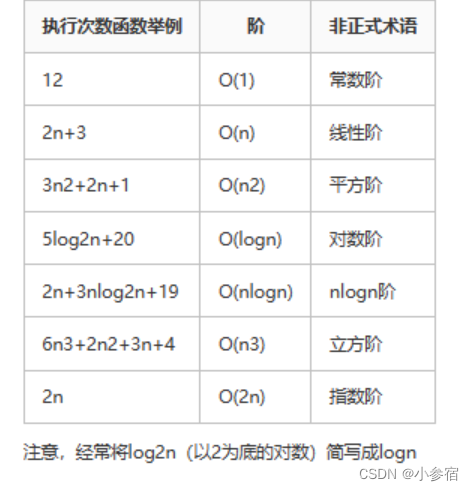
二.常见复杂度对比
总结:
这就是时间复杂度和空间复杂度的全部知识!希望对大家有所帮助
更新不易,辛苦各位小伙伴们动动小手,👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要!最后,本文仍有许多不足之处,欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正!
专栏订阅:
每日一题
c语言学习
算法
智力题
初阶数据结构
更新不易,辛苦各位小伙伴们动动小手,👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要!最后,本文仍有许多不足之处,欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正!