李宏毅2017机器学习课程 P3 回归 Regression
- 下文不区分w和ω(
文章目录
- 李宏毅2017机器学习课程 P3 回归 Regression
- 回归定义
- 举例:Pokemon精灵攻击力预测(Combat Power of a Pokemon)
- 模型步骤
- Step1:模型假设-线性模型
- 一元线性模型(单个特征)
- 多元线性模型(多个特征)
- Step2:模型评估-损失函数
- 收集和查看训练数据
- 如何判断众多模型的好坏
- Step 3:最佳模型 - 梯度下降
- 解决单个参数
- 解决两个参数
- 梯度下降推演最优模型的过程
- 梯度下降算法在现实世界中面临的挑战
- w和b偏微分的计算方法
- 如何验证训练好的模型的好坏
- 更强大复杂的模型:1元N次线性模型
- 考虑更复杂的模型,过拟合问题出现
- 步骤优化
- Step1优化:2个input的四个线性模型是合并到一个线性模型中
- Step2优化:如果希望模型更强大表现更好(更多参数,更多input)
- Step3优化:加入正则化(regularization)
- 总结
回归定义
- 找到一个函数function,通过输入特征x,输出一个数值scalar
举例:Pokemon精灵攻击力预测(Combat Power of a Pokemon)
李宏毅老师真是太有趣了哈哈哈哈
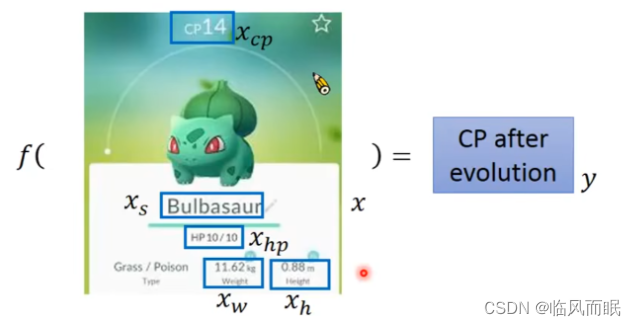
-
输入:进化前的CP值、物种(Bulbasaur)、血量(HP)、重量(Weight)、高度(Height)
-
输出:进化后的CP值
模型步骤
- 模型假设,选择模型框架(线性模型)
- 模型评估,如何判断众多模型的好坏(损失函数)
- 模型优化,如何筛选最优的模型(梯度下降)
Step1:模型假设-线性模型

一元线性模型(单个特征)
-
以一个特征 x c p x_{cp} xcp为例,线性模型假设 y = b + w ⋅ x c p y = b + w·x_{cp} y=b+w⋅xcp ,所以 ω \omega ω 和 b b b 可以猜测很多模型,比如
f 1 : y = 10.0 + 9.0 ⋅ x c p f 2 : y = 9.8 + 9.2 ⋅ x c p f 3 : y = − 0.8 − 1.2 ⋅ x c p ⋅ ⋅ ⋅ f_1: y = 10.0 + 9.0·x_{cp} \\ f_2: y = 9.8 + 9.2·x_{cp} \\ f_3: y = - 0.8 - 1.2·x_{cp} \ ··· f1:y=10.0+9.0⋅xcpf2:y=9.8+9.2⋅xcpf3:y=−0.8−1.2⋅xcp ⋅⋅⋅
-
虽然可以做出很多假设,但在这个例子中,显然 f 3 : y = − 0.8 − 1.2 ⋅ x c p f_3: y = - 0.8 - 1.2·x_{cp} f3:y=−0.8−1.2⋅xcp 的假设是不合理的,不能进化后CP值是个负值吧~~
多元线性模型(多个特征)
-
在实际应用中,输入特征肯定不止 x c p x_{cp} xcp 这一个。例如,进化前的CP值、物种(Bulbasaur)、血量(HP)、重量(Weight)、高度(Height)等,特征会有很多
-
所以我们假设 线性模型 Linear model: y = b + ∑ w i x i y = b + \sum w_ix_i y=b+∑wixi
-
x i x_i xi:就是各种特征(fetrure) x c p , x h p , x w , x h , ⋅ ⋅ ⋅ x_{cp},x_{hp},x_w,x_h,··· xcp,xhp,xw,xh,⋅⋅⋅
-
ω i \omega_i ωi:各个特征的权重 ω c p , ω h p , ω w , ω h , ⋅ ⋅ ⋅ \omega_{cp},\omega_{hp},\omega_w,\omega_h,··· ωcp,ωhp,ωw,ωh,⋅⋅⋅
-
b b b:偏移量
-
注意:接下来的内容需要看清楚是【单个特征】还是【多个特征】的示例
Step2:模型评估-损失函数
【单个特征】: $x_{cp} $
收集和查看训练数据
-
这里定义 x 1 x^1 x1 是进化前的CP值, y ^ 1 \hat{y}^1 y^1 进化后的CP值, ^ \hat{} ^ 所代表的是真实值
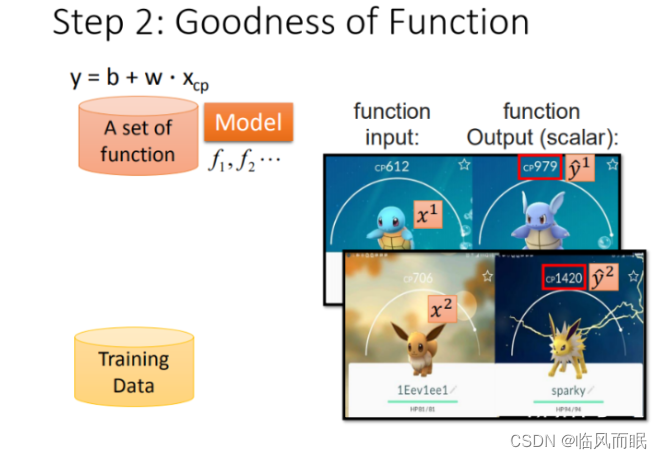
-
将10组原始数据在二维图中展示,图中的每一个点 $(x_{cp}n,\hat{y}n) $ 对应着进化前的CP值 和 进化后的CP值
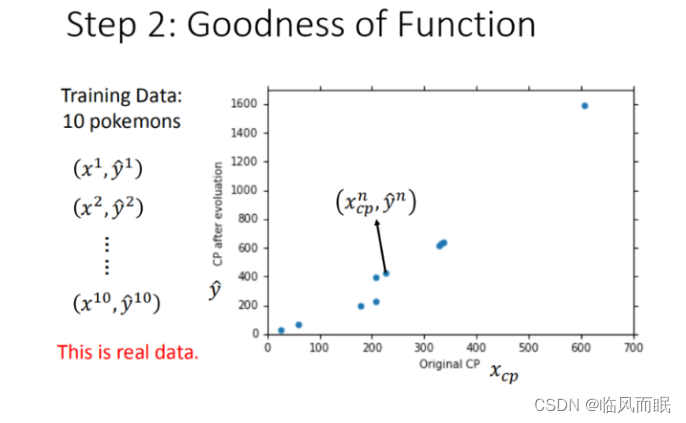
如何判断众多模型的好坏
-
有了这些真实的数据,那我们怎么衡量模型的好坏呢?从数学的角度来讲,我们使用距离。求【进化后的CP值】与【模型预测的CP值】差,来判定模型的好坏。也就是使用损失函数(Loss function) 来衡量模型的好坏,统计10组原始数据 $\left ( \hat{y}^n - f(x_{cp}^n) \right )^2 $ 的和,和越小模型越好。如下图所示:

L ( f ) = ∑ n = 1 10 ( y ^ n − f ( x c p n ) ) 2 , 将 [ f ( x ) = y ] , [ y = b + w ⋅ x c p ] 代 入 = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p ) ) 2 \begin{aligned} L(f)&=\sum\limits_{n=1}^{10} (\hat{y}^n-f(x_{cp}^n))^2,将[f(x)=y],[y=b+w·x_{cp}]代入 \\&=\sum\limits_{n=1}^{10}(\hat{y}^n-(b+w·x_{cp}))^2\end{aligned} L(f)=n=1∑10(y^n−f(xcpn))2,将[f(x)=y],[y=b+w⋅xcp]代入=n=1∑10(y^n−(b+w⋅xcp))2
-
最终定义 损失函数 Loss function:

L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p ) ) 2 L(w,b)= \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2 L(w,b)=n=1∑10(y^n−(b+w⋅xcp))2
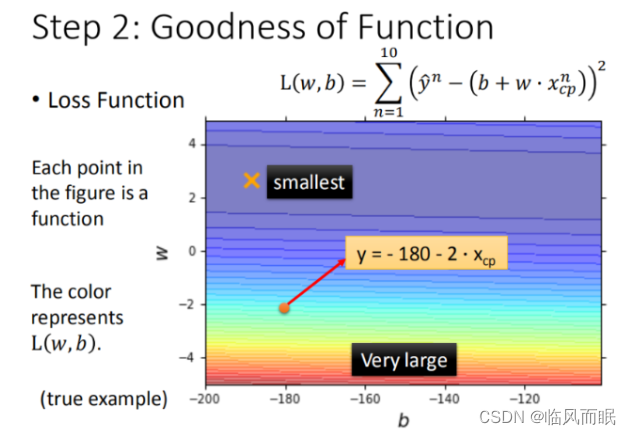
- 图中每一个点代表着一个模型对应的 w w w 和 b b b
Step 3:最佳模型 - 梯度下降
- 目标:筛选最优模型(参数 ω , b \omega,b ω,b)
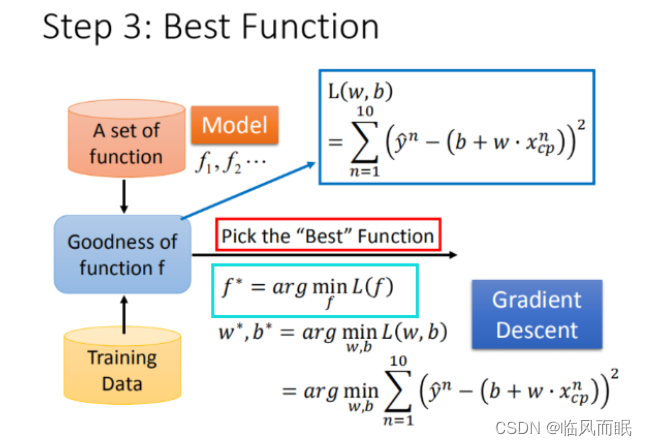
-
对上图的解释:
已知损失函数是
L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p ) ) 2 L(w,b) = \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2 L(w,b)=n=1∑10(y^n−(b+w⋅xcp))2
需要找到一个令结果 L ( f ) L(f) L(f)最小的 f f f,记作 f ∗ f^* f∗,或者说使得结果最小的 w w w和 b b b,记作 w ∗ , b ∗ w^*,b^* w∗,b∗
解决单个参数
-
如何筛选:梯度下降
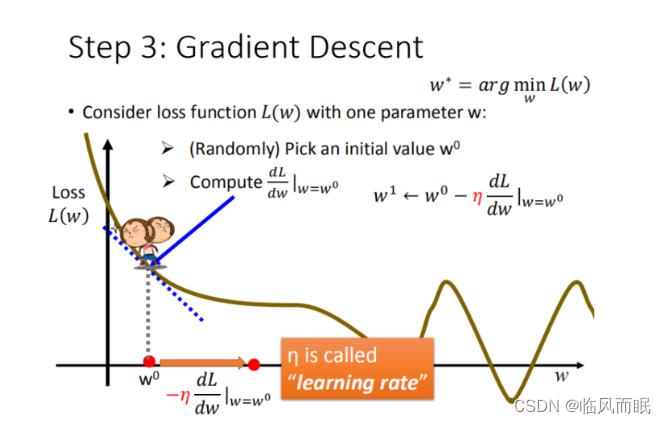
-
学习率 :移动的步长,如图中 η \eta η
-
先随机选取一个初始点 ω 0 {\omega}^0 ω0
-
计算 d L d w ∣ w = w 0 \dfrac{dL}{dw}|_{w=w^0} dwdL∣w=w0
更新 ω \omega ω,前面是要乘以一个- η η η
- 当前斜率大于0,减少w的值
- 斜率小于0,增加w的值
-
根据学习率移动
-
重复2和3
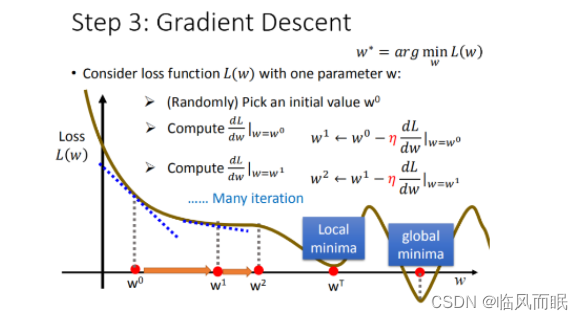
步骤1中,我们随机选取一个 w 0 w^0 w0,如上图所示,我们有可能会找到当前的最小值(局部最优),并不是全局的最小值,这里我们保留这个疑问,后面解决。
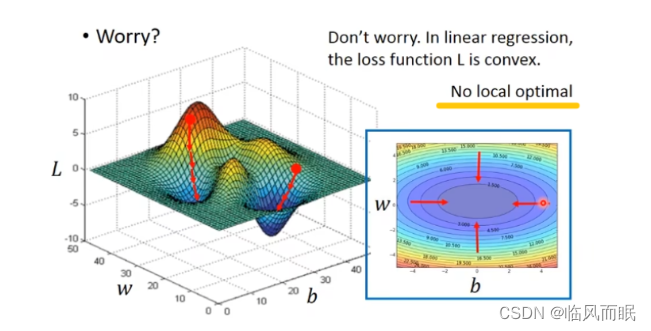
loss function L is convex(凸函数)
解决两个参数
- 解释完单个模型参数 ω \omega ω,引入2个模型参数 ω \omega ω 和 b b b , 其实过程是类似的,需要做的是偏微分,过程如下图

- 引入算子
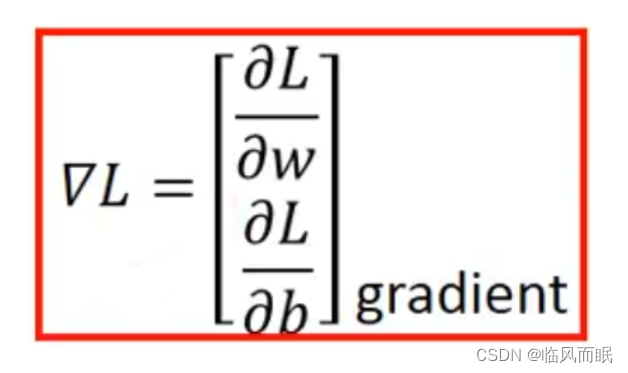
梯度下降推演最优模型的过程
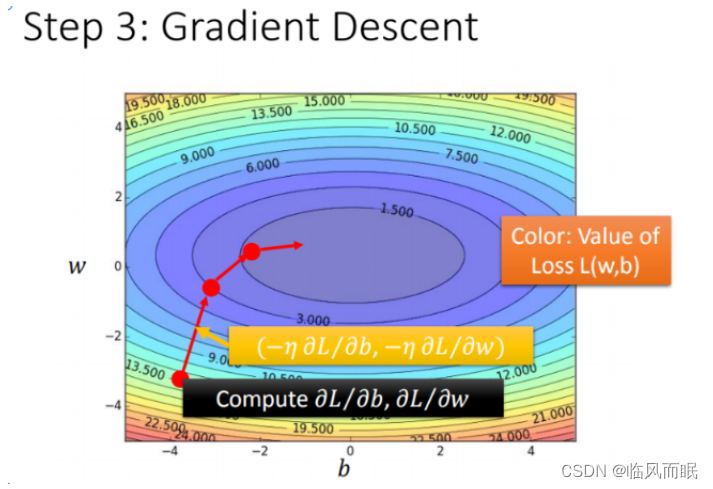
-
每一条线围成的圈就是等高线,代表损失函数的值,颜色约深的区域代表的损失函数越小
想到了高中电场学的等势线,电场线方向是电势降低最快的方向, 电场强度是电势的负梯度
把上面那个轨迹看成电荷挺好玩的,它在寻求低势
-
红色的箭头代表等高线的法线方向
梯度下降算法在现实世界中面临的挑战
-
我们通过梯度下降gradient descent不断更新损失函数的结果,这个结果会越来越小,那这种方法找到的结果是否都是正确的呢?前面提到的当前最优问题外,还有没有其他存在的问题呢?

其实还会有其他的问题:
-
问题1:当前最优(Stuck at local minima)
-
问题2:等于0(Stuck at saddle point)
-
问题3:趋近于0(Very slow at the plateau)
-
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TKEOmi3n-1669429689091)(https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20221126101632.png)]
注意:其实在线性模型里面都是一个碗的形状(山谷形状),梯度下降基本上都能找到最优点(不会stuck at local minima),但是再其他更复杂的模型里面,就会遇到 问题2 和 问题3 了
w和b偏微分的计算方法

如何验证训练好的模型的好坏
- 使用训练集和测试集的平均误差来验证模型的好坏 我们使用将10组原始数据,训练集求得平均误差为31.9,如图所示:
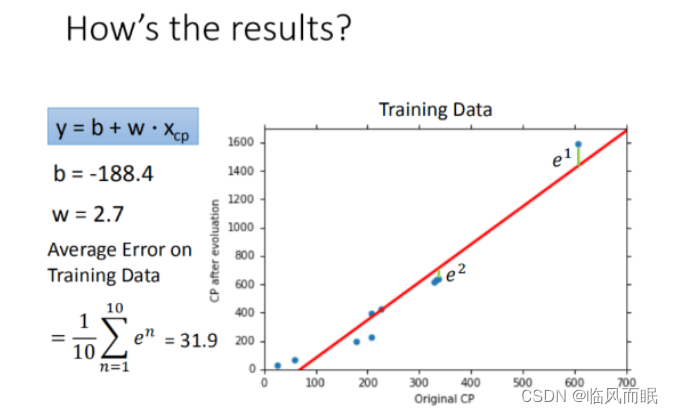
- 然后再使用10组Pokemons测试模型,测试集求得平均误差为35.0 如图所示:
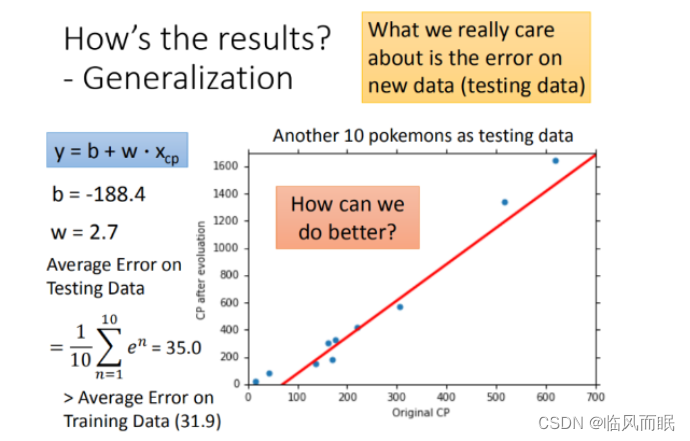
-
此时,模型还需要优化,需要一个更复杂的model
更强大复杂的模型:1元N次线性模型
-
在模型上,我们还可以进一步优化,选择更复杂的模型,使用1元2次方程举例,还是根据training data,利用gradient descent,求出best function
-
求出best function之后,来验证模型的好坏,发现训练集求得平均误差为15.4,测试集的平均误差为18.4
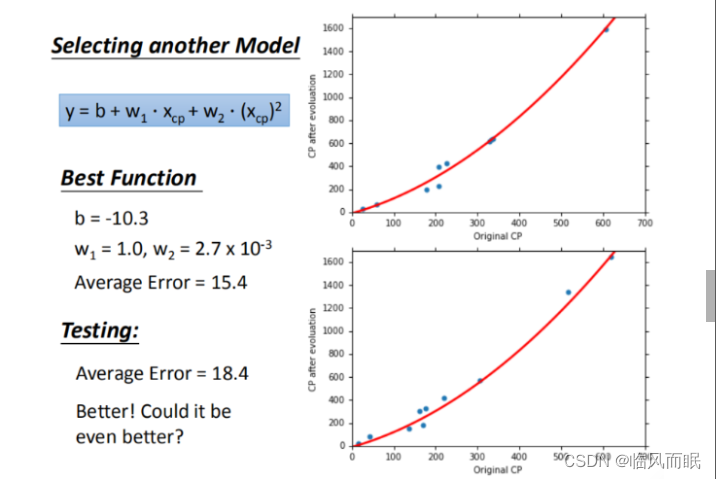
- leeml notes👇

考虑更复杂的模型,过拟合问题出现
在模型上,我们再可以进一部优化,使用更高次方的模型,如图所示
-
训练集平均误差【15.4】【15.3】【14.9】【12.8】
-
测试集平均误差【18.4】【18.1】【28.8】【232.1】
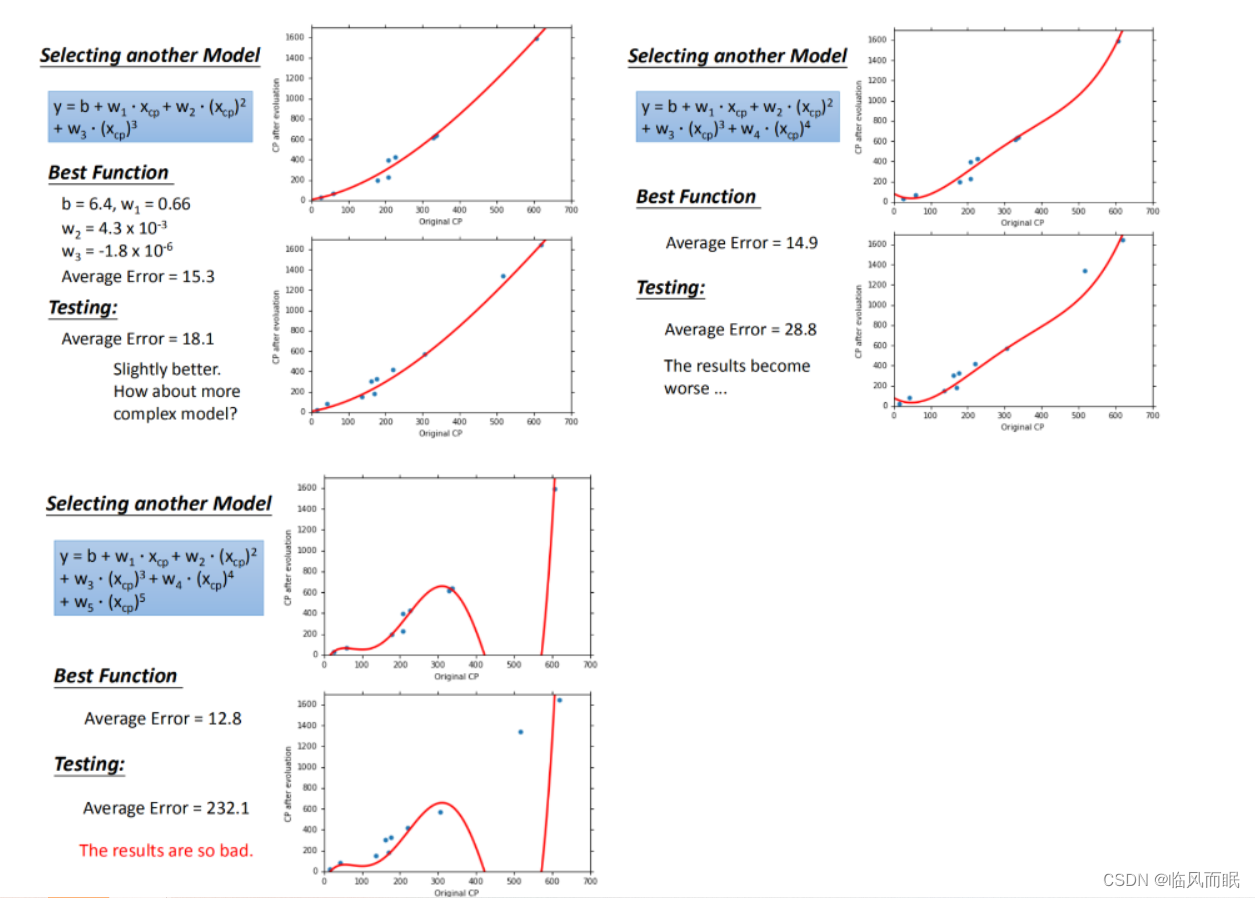
在训练集上面表现更为优秀的模型,为什么在测试集上效果反而变差了?这就是模型在训练集上过拟合的问题
-
如图所示,每一个模型结果都是一个集合,5次模型 ⊇ \supseteq ⊇ 4次模型 ⊇ \supseteq ⊇ 3次模型

- 将错误率结果图形化展示,发现3次方以上的模型,已经出现了过拟合的现象:

- 选择3次的目前较为合理
步骤优化
- 输入更多Pokemons数据,相同的起始CP值,但进化后的CP差距竟然是2倍。如图,其实将Pokemons种类通过颜色区分,就会发现Pokemons种类是隐藏得比较深的特征,不同Pokemons种类影响了进化后的CP值的结果
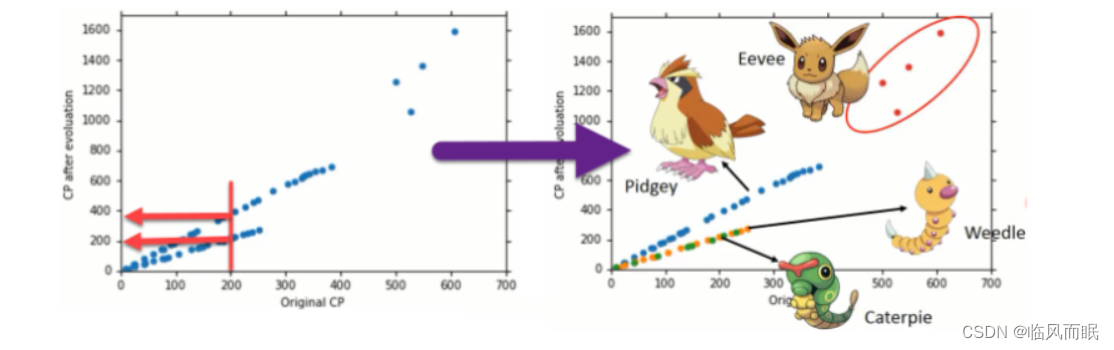
Step1优化:2个input的四个线性模型是合并到一个线性模型中
- 通过对 Pokemons种类判断,将 4个线性模型合并到一个线性模型中
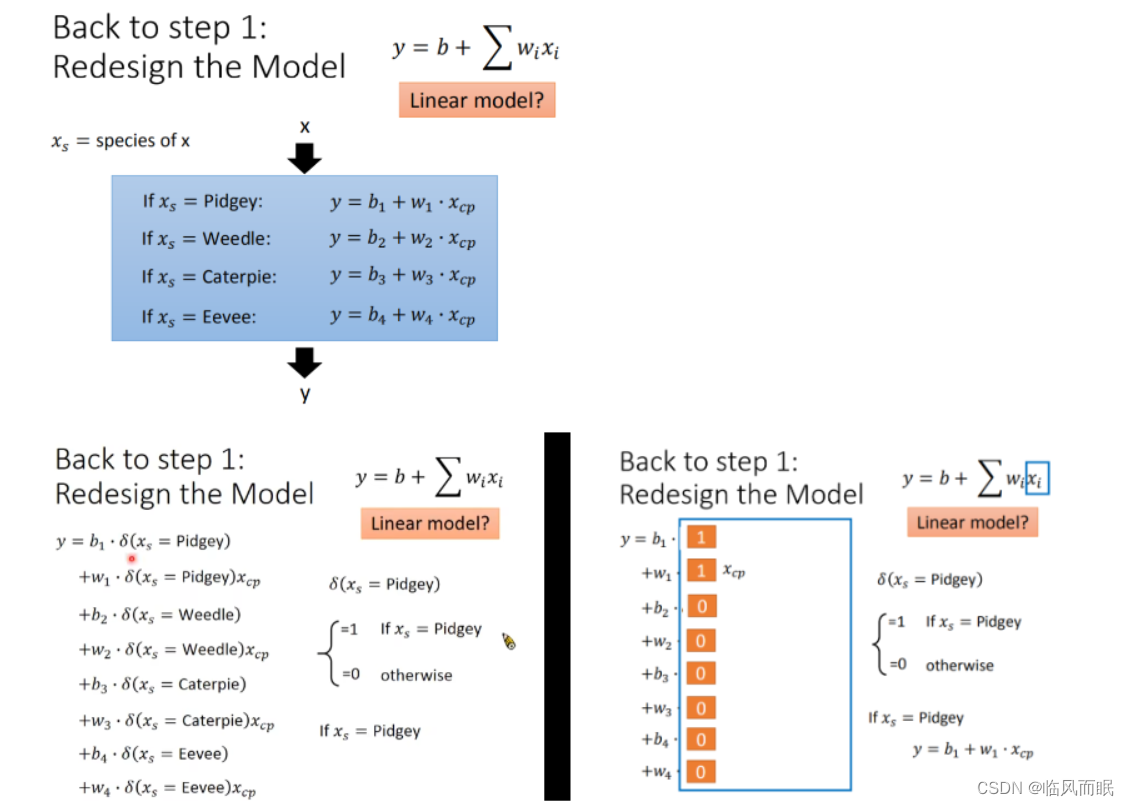
-
不同种类的宝可梦,参数不一样,按这个思路来考虑
error如下 训练数据3.8 测试数据14.3

Step2优化:如果希望模型更强大表现更好(更多参数,更多input)
-
在最开始我们有很多特征,图形化分析特征,将血量(HP)、重量(Weight)、高度(Height)也加入到模型中
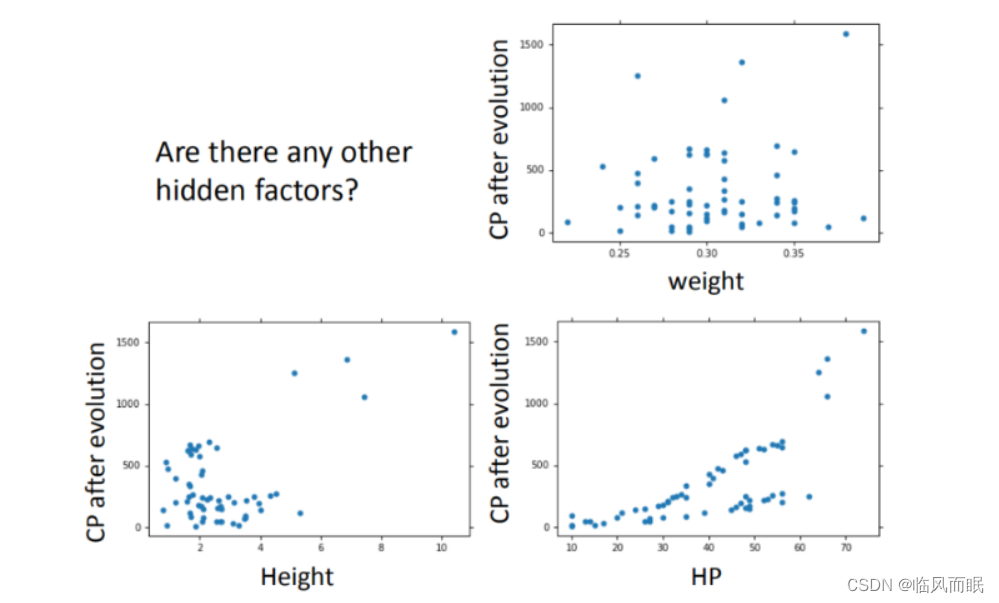
-
弄一个function
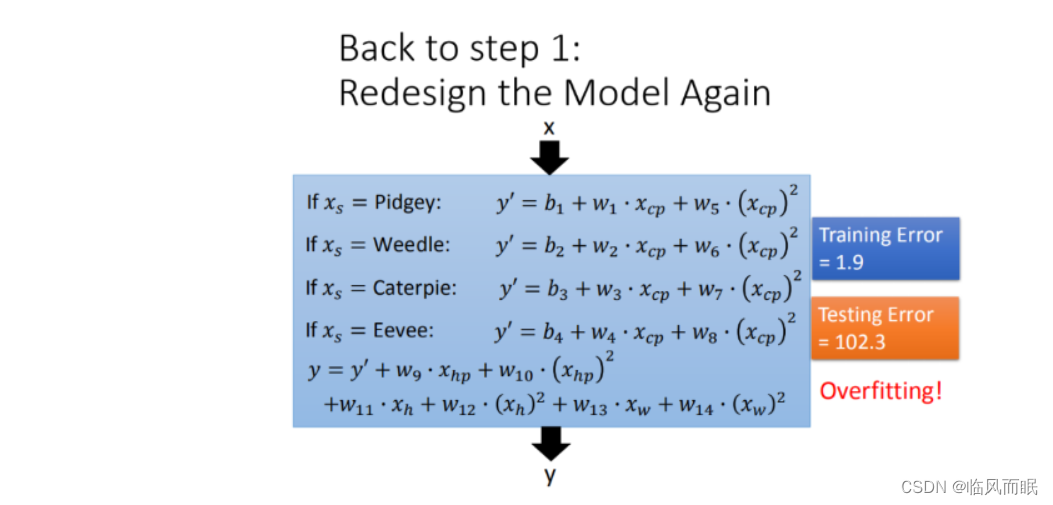
更多特征,更多input,数据量没有明显增加,仍旧导致overfitting
Step3优化:加入正则化(regularization)
- 更多特征,但是权重 w w w可能会使某些特征权值过高,仍旧导致overfitting,所以加入正则化
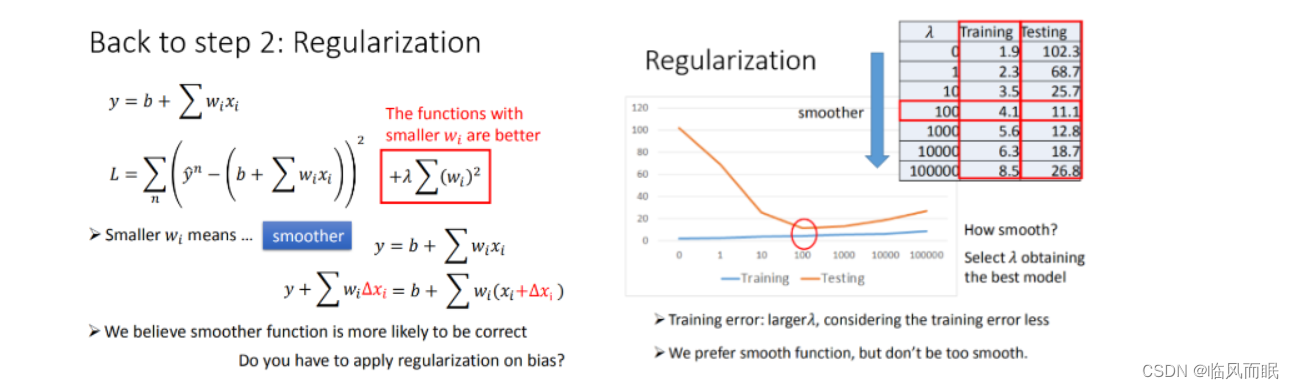
-
w 越小,表示 function 较平滑的, function输出值与输入值相差不大
-
在很多应用场景中,并不是 w 越小模型越平滑越好,但是经验值告诉我们 w越小大部分情况下都是好的。
-
b的值接近于0 ,对曲线平滑是没有影响
总结







![[附源码]java毕业设计智能超市导购系统](https://img-blog.csdnimg.cn/115bad91fc904e0a91a29db6cabb1cce.png)