目录

3.3.2 Proofs by Reduction

最后来理一遍：

---

3.3.2 Proofs by Reduction

如果我们希望证明一个给定的构造（例如，加密方案）在计算上是安全的，那么——除非该方案在信息理论上是安全的——我们必须依赖于未经证明的假设。我们的策略是假设一些数学问题是困难的，或者一些低级的密码原语是安全的，然后证明只要我们的初始假设是正确的，基于该问题/原语的给定构造是正确的。

我们首先假设一些问题X不能用任何多项式时间算法来解决(除了可以忽略的概率)。

归约证明的步骤：

确定一些有效的（即概率多项式时间）敌手A攻击Π。用ε(n)表示这个敌手的成功概率。

使用A作为子程序构造一个有效的算法A’试图解决问题X。A’对A是如何工作的一无所知；A’唯一知道的是A期望攻击Π。给定问题X的一些输入实例x，算法A’将其模拟为对于A的实例Π

当A作为A’的子程序的时候的运行环境应该和当A和Π进行互动的时候的运行环境一致

当A成功地破解了被A’模拟的Π实例，这意味着A’可以解决实例x，当然，A’解决以x作为实例输入的数学难题X的概率应至少为概率多项式的倒数1/p(n)

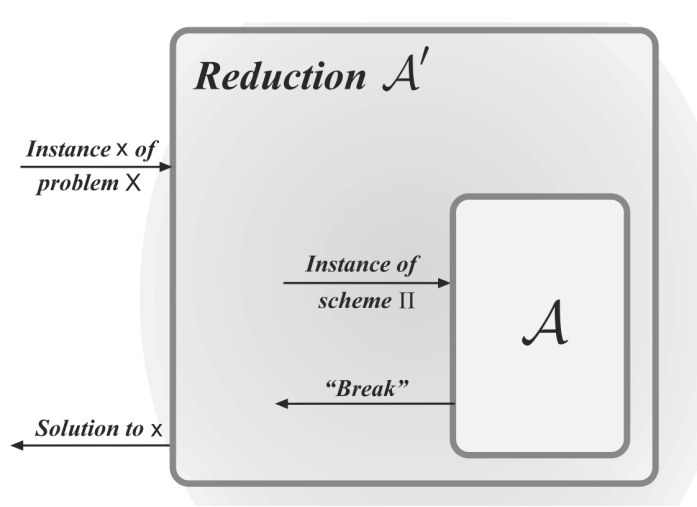
综上所述，说明A’解决X的概率为ε(n)/p (n)。如果ε(n)是不可忽略，那么ε(n)/p (n)也不可忽略。此外，如果A是有效的，那么我们得到了一个有效的算法A’有不可忽略的概率求解X，与我们的初始假设相矛盾。

鉴于我们关于X的假设，我们得出结论，没有一个有效的对手A能够以不可忽略的概率成功地打破Π。换句话说，Π是计算安全的。

---

最后来理一遍：

• 假设某个问题X（比如某数学难题）不能用任何多项式时间算法来解决
• 解决问题X可以通过多项式次调用Π来实现
• 如果Π可以在多项式时间内解决，根据多项式的闭包性质，那么X就能在多项式时间内解决
• 这显然与假设矛盾
• 因此Π也不能在多项式时间内解决