CRC校验码,顾名思义是用于校验的。它可以用于检测数据传输过程中是否出现错误(某些位,或某几位,或者某块区域位错误),反正 可以知道数据出错了,但是不能纠错。
CRC校验,本质上是模2除法求余。将发送信息M当做被除数,发送方和接收方共同约定一个除数G
(可以随机选择,也可以使用国际标准,但是最高位和最低位必须为1)
,然后求余R,该余数R即为CRC值。
然而在 verilog实现的时候却并不会通过最原始的模2除法实现,而是用串行CRC电路来实现,这本质上也是一种模2除法。下面我将指出两种方法的一致性以便于记录和理解:
理论思路
- 模2除法
- 串行CRC电路
- 总结
在描述CRC校验的流程之前,需要先描述一下模2除法
模2除法
模2除法可以说和二进制除法没什么关系,千万不要搞混了。它的计算其实也很简单,就是简单的移位和异或处理。
模2除法有三个准则:
- 被除数的首位为1,则商的该位为1。被除数的首位为0,则商的该位为0。
- 减法运算时需要模2减,即异或操作。
- 当被除数的位数小于除数,计算结束。
为便于理解,我们举个例子。
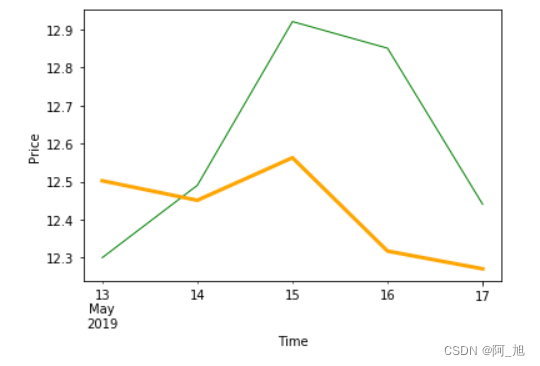
假设原始数据M为 1101011011
多项式为
x
4
+
x
+
1
x^4 + x + 1
x4+x+1
可以得到除数G为 10011
首先在原始数据后面添加4个0(因为多项式是5位,添加5-1=4位)
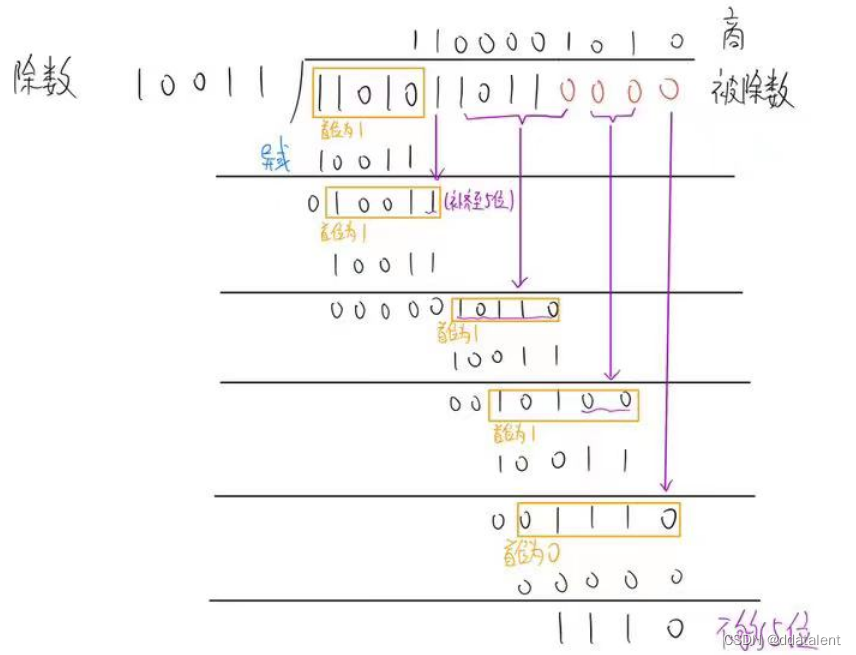
上图为计算流程,图中很多次涉及到被除数的首位为0,则该商的该位为0的计算时,都略过了,只有最后一次没有略过,但是依然是便于理解的。
最终得到商为 1100001010
余数R为 1110
因为多项式是5位的,所以得到的校验位是5-1=4位的。余数R恰好为4位,无需在前面补0。因此哦我们得到校验位就是1110。
CRC模块的输出就是1101011011 1110
串行CRC电路
在FPGA中该如何实现CRC校验的工作呢?仔细观察上面的操作,可以发现,CRC校验码的计算,相当于是把多项式和原始数据左对齐,然后按位进行异或、再把多项式右移到新的1处,如此重复的操作,最终可以得到一个余数。
在电路里,右移和异或都是很基本的操作,只要了解该原理,我们就可以尝试复现该算法。
描述不清,我们直接看刚刚的例子
假设原始数据M为 1101011011
多项式为
x
4
+
x
+
1
x^4 + x + 1
x4+x+1
可以得到除数G为 10011
老样子,首先在原始数据后面添加4个0(因为多项式是5位,添加5-1=4位)。
- 第一步
1 1 0 1 0 | 1 1 0 1 1 0 0 0 0 //原始数据串
1 0 0 1 1 //多项式,左对齐,二者进行按位异或
-------------------------------
0 1 0 0 1 //第一次异或结果
- 第二步
0 | 1 0 0 1 1 | 1 0 1 1 0 0 0 0 //第一次异或结果和原始数据串中未操作的数合并得到新的数据串
1 0 0 1 1 //多项式右移到下一个1处,再次按位异或
-------------------------------
0 0 0 0 0 //第二次异或结果
- 第三步
0 0 0 0 0 0 | 1 0 1 1 0 | 0 0 0 //第二次异或结果和原始数据串中未操作的数合并得到新的数据串
1 0 0 1 1 //多项式右移到下一个1处,再次按位异或
-------------------------------
0 0 1 0 1 //第三次异或结果
- 第四步
0 0 0 0 0 0 0 0 | 1 0 1 0 0 | 0 //第三次异或结果和原始数据串中未操作的数合并得到新的数据串
1 0 0 1 1 //多项式右移到下一个1处,再次按位异或
-------------------------------
0 0 1 1 1 //第四次异或结果
- 第五步
0 0 0 0 0 0 0 0 0 0 1 1 1 0 //第四次异或结果和原始数据串中未操作的数合并得到新的数据串
1 0 0 1 1 //多项式右移到到下一个1处,发现移不过去,于是结束
-------------------------------
得到最终结果之后,因为一开始在数据串后面添加了4个0,所以这里保留低4位,得到校验码1110,加在数据串后面得到1101011011 1110。
仔细看完这一步操作,细细思索就会发出疑问:多项式右移到下一个1处 这一关键的步骤是怎么实现的呢?
其实很简单,我们只需要记住:对于10011这个多项式来说,和数据做异或就是把数据的最高位(即第五位)和低两位(即第一第二位)做翻转。
当数据为0开头的时候,我们不想翻转。当数据为1的时候我们想要翻转。那我们就把输入数据的最高位也加入运算当中去即可(众所周知,在异或操作中,1代表翻转,0代表不翻转)
譬如当多项式右移到0开头的位置的时候
0 1 1 1 0 //某数据串
1 0 0 1 1 //多项式
-------------------------------
1 1 1 0 1
这个时候应该是跳过的,为了让数据恢复原样,我们就把结果的最高位和低两位与原始数据的最高位取反后的结果进行异或即可
1 1 1 0 1 //某数据串
1 1 1 //多项式
-------------------------------
0 1 1 1 0
而当多项式右移到1开头的位置的时候
1 1 1 1 0 //某数据串
1 0 0 1 1 //多项式
-------------------------------
0 1 1 0 1
这个时候应该是正确的,但是我们也同样可以把结果的最高位和低两位与数据的最高位进行异或
0 1 1 0 1 //某数据串
0 0 0 //多项式
-------------------------------
0 1 1 0 1
总结
比较模2除法和CRC串行电路两种方法,其实大同小异。但是如果不从电路的视角来理解,会觉得二者差异很大。个人比较偏向于CRC串行电路的理解方法,直观且便于实现。
解CRC就重复加CRC的步骤即可。
本文参考:
- B站视频
- 其他人的博客