前言

1、最长公共子序列
2、不相交的线
3、最大子序和
4、判断子序列

一、最长公共子序列（力扣1143）

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列，返回 0 。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的公共子序列是这两个字符串所共同拥有的子序列。
在这里插入图片描述
分析：
感觉类似于单词拆分问题
单词拆分问题
1、dp[i]数组以及下标含义
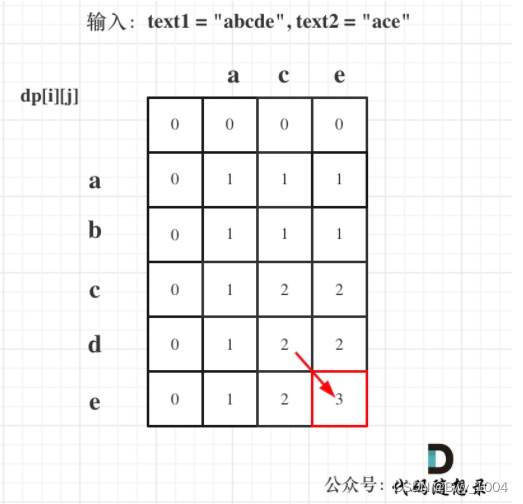
dp[i][j]: 以i-1为结尾的text1子数组和以j-1为结尾的text2子数组的最长公共子序列长度。
这样定义的好处可以节省初始化里面的过程
2、递推公式
if(nums1[i-1]==nums2[j-1])
dp[i][j] = dp[i-1][j-1]+1;
else dp[i][j] = max(dp[i-1][j], dp[i][j-1])
3、初始化
dp[0][j] = 0;
dp[i][0] = 0;
4、遍历顺序
先遍历哪个字符串都可以从前向后
5、举例推导dp数组
以输入：text1 = “abcde”, text2 = “ace” 为例，dp状态如图：
在这里插入图片描述

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
       

        char[] char1 = text1.toCharArray();
        char[] char2 = text2.toCharArray();

        int[][] dp = new int[char1.length+1][char2.length+1];

        for(int i=1;i<=char1.length;i++){
            for(int j=1;j<=char2.length;j++){
                if(char1[i-1]==char2[j-1]){
                    dp[i][j] = dp[i-1][j-1]+1;
                }
                else dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[char1.length][char2.length];
    }
}

在这里插入图片描述

二、不相交的线（力扣1035）

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

nums1[i] == nums2[j]
且绘制的直线不与任何其他连线（非水平线）相交。
请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。
在这里插入图片描述
分析：
与上一题几乎一模一样
说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length+1][nums2.length+1];
        for(int i=1;i<=nums1.length;i++){
            for(int j=1;j<=nums2.length;j++){
                if(nums1[i-1]==nums2[j-1])
                    dp[i][j] = dp[i-1][j-1]+1;
                else dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[nums1.length][nums2.length];
    }
}

在这里插入图片描述

三、最大子序和（力扣53）

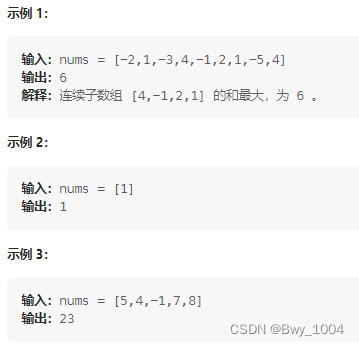
给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。
在这里插入图片描述
分析：
之前用贪心算法已经求解过
贪心算法求解

通过动态规划求解：
1、确定dp数组以及下标的含义
dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]。
2、递推公式
dp[i]只有两个方向可以推出来：

dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
nums[i]，即：从头开始计算当前连续子序列和

dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);
3、初始化
dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础。
dp[0] = nums[0]
4、遍历顺序
从前向后遍历

class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int res = dp[0];
        for(int i=1;i<nums.length;i++){
            dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);
            res = Math.max(res,dp[i]);

        }
        return res;
    }
}

在这里插入图片描述

四、判断子序列（力扣392）

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）
在这里插入图片描述

暴力求解：

class Solution {
    public boolean isSubsequence(String s, String t) {
        int index = -1;
        for (char c : s.toCharArray()){
            index = t.indexOf(c, index+1);
            if (index == -1) return false;
        }
        return true;
    }
}

动态规划求解：
1、dp[]数组以及下标含义
dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。
2、递推公式
if(s[i-1]==t[j-1])
dp[i][j] = dp[i-1][j-1]+1
else
dp[i][j] = dp[i][j-1]

参考最长公共子序列（力扣1143）
3、初始化
dp[0][j] = 0;
dp[i][0] = 0;
4、遍历顺序
先遍历哪个字符串都可以从前向后

class Solution {
    public boolean isSubsequence(String s, String t) {
        char[] ss = s.toCharArray();
        char[] tt = t.toCharArray();
        int[][] dp = new int[ss.length+1][tt.length+1];
        for(int i=1;i<=ss.length;i++){
            for(int j=1;j<=tt.length;j++){
                if(ss[i-1]==tt[j-1])
                    dp[i][j] = dp[i-1][j-1]+1;
                else
                    dp[i][j] = dp[i][j-1];
            }
        } 
        return dp[ss.length][tt.length]==ss.length;
    }
}