题目链接：无

1. 题目介绍（10- Ⅲ. 矩形覆盖 ）

我们可以用2x1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2x1的小矩形无重叠地覆盖一个2xn的大矩形，总共有多少种方法？

【测试用例】：
示例 1：

输入：n = 2
输出：2

示例 2：

输入：n = 8
输出：34

【条件约束】：

提示：

• 0 <= n <= 100

【拓展题目】：

• LCP 04. 覆盖
  你有一块棋盘，棋盘上有一些格子已经坏掉了。你还有无穷块大小为1 * 2的多米诺骨牌，你想把这些骨牌不重叠地覆盖在完好的格子上，请找出你最多能在棋盘上放多少块骨牌？这些骨牌可以横着或者竖着放。

2. 题解

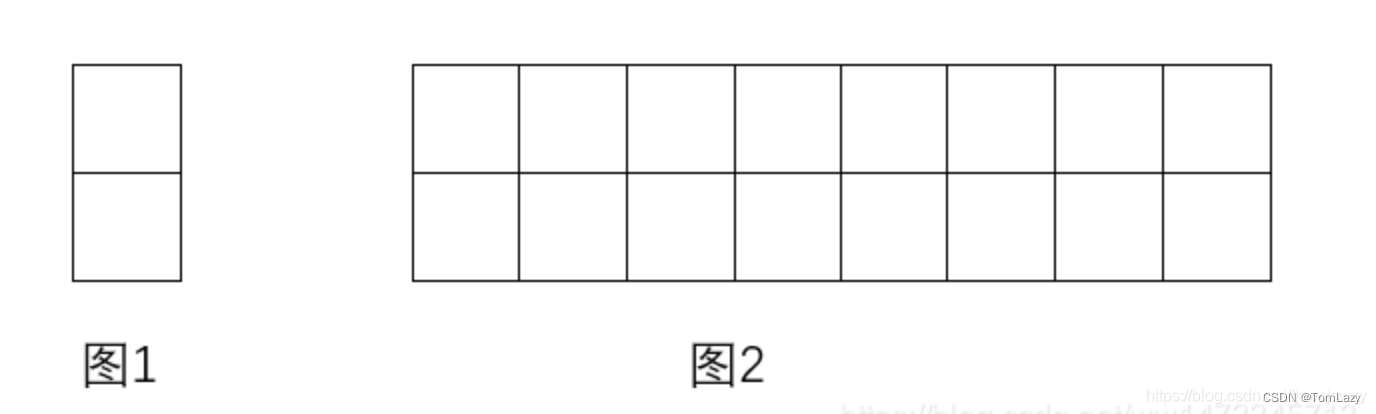
该题的本质依旧是 斐波那契数列 的应用

当n=1时，只有1种；当n=2时，有2种；
当n>2时，如果竖着放最后一列，则结果为n-1的结果；横着放就是n-2的结果；
所以最后的结果为f(n) = f(n-1) + f(n-2)；还是一个斐波那契数列

把覆盖2x8矩形的覆盖方法总数记为f(8).用第一个矩形去覆盖大矩形时，有两种选择，横放或者竖放。竖放时，右边有2x7的区域尚未被覆盖，那么剩下区域覆盖方法的总数为f(7)。

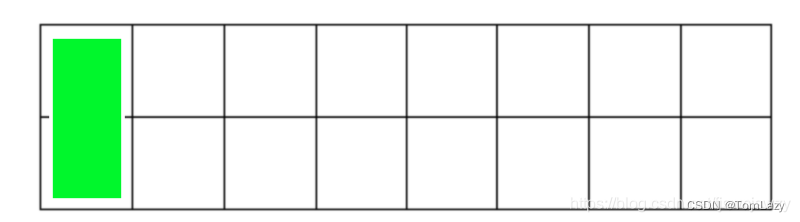
第一个矩形横向的情况下，必须占用另外一个小矩形去覆盖左下角。此时就能确定最左边2x2的格子了，因此右边还剩下2x6的区域尚未被覆盖，记为f(6)。

因此可以得出关系， f(8) = f(7) + f(6)。显然我们也知道f(1)=1,f(2) = 2.

2.1 递归法 – O(2ⁿ)

时间复杂度O(2ⁿ)，空间复杂度O(1)

public static long RectCover1(int target) {
   if(target < 3)return target;
   return RectCover(target - 1) + RectCover(target - 2);
  }

2.2 非递归 – O(n)

时间复杂度O(n)，空间复杂度O(1)

public static long RectCover(int target) {
   if(target < 3)return target;
   long pre1 = 1;
   long pre2 = 2;
   
   for(int i = 3; i<= target; i++){
    long sum = pre1 + pre2;
    pre1 = pre2;
    pre2 = sum;
   }
   return pre2;
  }

3. 参考资料

[1] 【LeetCode】剑指 Offer 10- I. 斐波那契数列 p74 – Java Version
[2] 【LeetCode】剑指 Offer 10- II. 青蛙跳台阶问题 p77 – Java Version
[3] LeetCode之矩形覆盖 – （代码来源）
[4] (java)矩形覆盖:我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？ – 部分图片来源