基于信息论的熵值法是根据各指标所含信息有序程度的差异性来确定指标权重的客观赋权方法，仅依赖于数据本身的离散程度。

熵用于度量不确定性，指标的离散程度越大（不确定性越大）则熵值越大，表明指标值提供的信息量越多，则该指标的权重也应越大。

1. 多属性决策问题

熵权法多用于多属性决策问题中求解各个属性的权值。我们先简单介绍下多属性决策：
多属性决策指的是在考虑多个属性的情况下，对一组（有限个）备选方案进行排序或者择优。
主要包含以下几个组成部分：
（1）获取属性信息。
（2）属性权重确定：包括主观赋权法、客观赋权法、主客观结合的赋权法。
（3）多属性决策：对决策所需的属性信息进行集结，并基于相应策略对备选方案进行排序和择优。

这里，假设我们的数据的样本数量为$n$，每个样本有$j$个feature，那么对于一个样本的一个feature的取值为： $x_{ij}$
其中：
$i$ ：第个样本
$j$ ：第个feature

假设有这样一个应用场景，由于每一个样本都有很多feature，我想把这个样本的这些feature总结为一个值，应该怎么做？即

我们有一万种方法能达到这个目的，有了这个值，我们就可以进行排名、比较等操作。所以，这个值还得有点实际意义，不能是瞎攒出来的一个数。

熵权法(EEM, entropy evaluation method)是根据指标信息熵的大小对指标客观赋值的一种方法，信息熵越大，代表该指标的离散程度很大，包含的信息就多，所赋予的权重就越大。也就是说，这个方法实际上关注的是变量的取值的多样性，取值大小差异越大的，即离散程度越高的，就说明这个feature的重要程度很大，包含了更多的信息。

2. 熵（entropy）

熵的概念是由德国物理学家克劳修斯于1865年所提出。最初是用来描述“能量退化”的物质状态参数之一，在热力学中有广泛的应用。

热力学第二定律又被称为”熵增“定律，从它的描述中大家也能明白一二：在自然状态下，热量只会从热水杯传递给冷水杯，这个过程是不可逆的，而”熵“则是这个不可逆过程的度量。换而言之，封闭系统的熵只会不变或增加，不会减少。关于“热力学熵”，最原始的宏观表达式是：

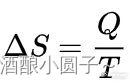
那时的熵仅仅是一个可以通过热量改变来测定的物理量，其本质仍没有很好的解释，直到统计物理、信息论等一系列科学理论发展，熵的本质才逐渐被解释清楚，即，熵的本质是一个系统“内在的混乱程度”。

3. 信息熵

信息熵是一个数学上颇为抽象的概念，由大名鼎鼎的信息论之父——克劳德 • 香农提出。在这里不妨把信息熵理解成某种特定信息的出现概率（离散随机事件的出现概率）。一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高。信息熵也可以说是系统有序化程度的一个度量。

一般说来，信息熵的表达式为：

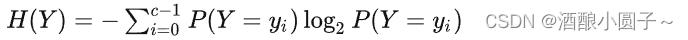
举例1：

假设一个硬币，投出正反两面的概率都是50%，那么它的entropy为：

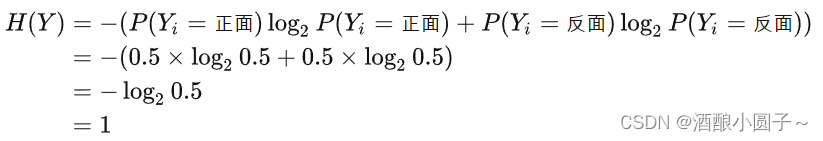
也就是说，一个公平的硬币，其正反面概率都是50%的情况下，熵最大化了。这件事推广到有多个面的骰子也是一样的，每个事件出现的概率越接近，样本的混乱程度就越高，熵就越大。而如果某个事件的出现概率是压倒性的，比其他所有事件出现概率加一起都高得多，那么熵就会比较小。

举例2：

假设4个元素，每个元素的feature有1个特征x1，并且它有个类型y，即

我们发现一个很有趣的现象，就是进行分组以后，熵降低了。这实际上就是决策树的基本原理，通过对属性进行分割，从而降低整体的混乱程度。即对一个属性的不同取值进行分组以后，每一组的混乱程度做个加权和，整体混乱程度要比分组之前的混乱程度还要低，也就是说每一组都更纯粹一些。

当然，这里计算entropy的$lo{g}_2$是以2为底，也可以以自然对数为底，函数图像形状是基本不变的。

4. 熵权法

回到最开始我们问的问题，就是我怎么对一大堆指标(feature)进行综合一下，形成一个综合的值。当然我们就是用简单的加权和来做，但是我们还希望这个值具有一定的代表性。这个代表性我们就视为该feature下取值的多样性，或者说离散程度。

也就是说，如果一张数据表有很多行数据，每个数据又有很多feature，**如果某个feature的取值大家都一样，这实际上也说明这个feature可以丢掉了，用什么数据训练模型它都没啥用。但如果这个feature的取值特别多，那么这么指标对于决策更有用。**因此我们如果要综合一个指标的话，我们就要给最多样化，即离散程度最高的feature以最高的权重。

主要计算步骤如下：

（1）归一化数据

这里对数据进行归一化，主要是消除量纲的影响。可以采用 min-max归一化或者mean-std归一化方法。
数据归一化方法可以参考博客：数据预处理——数据无量纲化（归一化、标准化）

这里以min-max归一化为例：

这里有几点需要注意的：

• 如果原始数据中，不同属性的取值在相近的量级上，$x_{max}$和$x_{min}$可以直接取所有数据的最大最小值。

X_std = (X - np.min(X)) / (np.max(X) - np.min(X)

• 如果原始数据中，不同属性的取值量级相差较大，可以考虑使用列归一化，即$x_{max}$和$x_{min}$取列数据的列最大值和列最小值。

X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))

• 如果原始数据中，某个属性的取值完全一样为$x_v$，min、max、x 均相等，则基于min-max归一化方法计算分子分母均为0，默认算出的该属性数据均为0。

该属性的取值大家都一样，对于决策没有作用，参与决策过程的权重理应很小很小。而归一化后的0值数据，经过信息熵的计算后，$P=1$， $log(P)=0$，$-P\ast log(P)=0$，$E=0$，安全权重系数计算公式，最后算出来的权值很大，不符合实际情况。

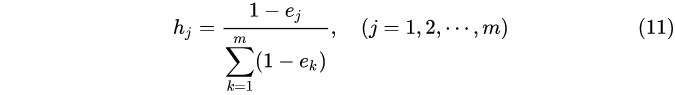
这种情况下，我们可以在数据归一化后，给数据加上一个很小的数值（比如1e-3）来避免样本取值为0情况，即：${x^{\prime \prime }}_{ij}=x_{ij}^{\prime }+0.001$

（2）只关注第$j$个feature，计算每个样本${x^{\prime \prime }}_{ij}$在第个feature下所占的全部取值的比例。

这个比例其实就是视为概率了。
举个例子，如果对于第$j$个feature，我们的样本经过归一化以后取值为：

我们可以理解为，取值越大，这个$p_{ij}$的值就越大。相当于我们自定义了一个"概率"，将其与取值联系到了一起，这么做，是因为我们要计算的熵仅仅与概率有关，而如果$x_{ij}$的取值特别多样化，我们用它算出来的这个概率也会特别多样化，有大有小，从而降低熵。

（3）计算第$j$个feature的熵。

（4）计算第$j$个feature的差异系数。

这个差异系数的含义显而易见，就是该feature的离散程度越高，该差异系数越高。

（5）对差异系数归一化，计算第个feature的权重

这样对于每个feature，其离散程度越高，所占比重就会越高。这样一来，我们就有了每个feature的权重了，下面我们用这个权重来算每个样本的指标

（6）计算最终的统计测度：

5. 熵权法的实现

先定义基础数据：

data = pd.DataFrame(
        {'人均专著': [0.1, 0.2, 0.4, 0.9, 1.2], '生师比': [5, 6, 7, 10, 2], '科研经费': [5000, 6000, 7000, 10000, 400],
         '逾期毕业率': [4.7, 5.6, 6.7, 2.3, 1.8]}, index=['院校' + i for i in list('ABCDE')])

【实现代码 1】：

import numpy as np

def get_entropy_weight_1(data): # 熵权法需要使用原始数据作为输入
	data = np.array(data)
	# 数据归一化
	# 这里可以根据需要选择mean-std归一化或者min-max归一化
	
    # 计算Pij
	P = data / data.sum(axis=0) # 需要考虑分子为0的情况，可以考虑加一个epsilon=1e-3

	# 计算熵值
	E = np.nansum(-P * np.log(P) / np.log(len(data)), axis=0)

	# 计算权系数
	return (1 - E) / (1 - E).sum()

get_entropy_weight_1(data)

程序输出结果：

array([ 0.41803075,  0.14492264,  0.28588943,  0.15115718])

【实现代码 2】：

def get_entropy_weight_2(data):
    """
    :param data: dataframe类型
    :return: 各指标权重列表
    """
    # 数据归一化
    # 这里可以根据需要选择mean-std归一化或者min-max归一化
    
    m,n=data.shape
    
    #将dataframe格式转化为matrix格式
    data=data.as_matrix(columns=None)
    
    # 第一步：计算k
    k=1/np.log(m)
    
    #第二步:计算pij
    pij=data/data.sum(axis=0)

    # 第三步：计算每种指标的信息熵
    tmp=np.nan_to_num(pij*np.log(pij))
    ej=-k*(tmp.sum(axis=0))
    
    # 第四步：计算每种指标的权重
    wi=(1-ej)/np.sum(1-ej)
    wi_list=list(wi)
    
    return  wi_list

get_entropy_weight_2(data)

[0.41803075156086411,
 0.14492263660659988,
 0.28588943395852595,
 0.15115717787401006]

可以看到，两个代码的输出结果一致，且各个属性的权值加起来和为1。

这里，有几个需要注意的点：

• 数据归一化：在原始数据量纲不一致时，我们使用熵权法之前可以先对数据做归一化处理。这里可以根据数据的实际情况和业务需要选择mean-std归一化或者min-max归一化。不同的归一化方法，对最后求出来的权值会有影响。
• 可以在数据归一化后，给数据加上一个很小的数值（比如1e-3）来避免样本取值为0情况，即：${x^{\prime \prime }}_{ij}=x_{ij}^{\prime }+0.001$
• 除数为0的情况：上述计算过程涉及除法，会遇到除数为0的情况。可以给除数加一个很小的数值，如epsilon=1e-3，以避免除以0的情况发生。

【参考博客】：

• TOPSIS法(优劣解距离法)介绍及 python3 实现
• https://zhuanlan.zhihu.com/p/551107230