文章目录
- refs
- 逻辑闸或逻辑门
- 与或非门
- 反相器和泡泡
- 与非/或非/异或
- 同或/是/蕴含/蕴含非
- 逻辑函数的表示方法及相互转换
- 逻辑表达式化简
- 基本公式
- 异或和同或的常用运算公式
refs
- digital_logic同或和异或的关系_xuchaoxin1375的博客-CSDN博客_异或与同或的关系
- 模2运算_模二除法和CRC循环冗余校验_xuchaoxin1375的博客-CSDN博客_模二运算
逻辑闸或逻辑门
-
逻辑闸或逻辑门是集成电路的基本组件。
-
简单逻辑门可由晶体管组成。这些晶体管的组合可以使代表两种信号的高低电平在通过它们之后产生高电平或者低电平的信号。
-
高,低电平可以分别代表逻辑上的“真”(T;true)与“假”(F;false)或二进制的1和0,从而实现逻辑运算。
-
常见的逻辑闸包括与闸,或门,非闸,异或闸(也称异或)。
-
逻辑闸是组成数字系统的基本结构,通常组合使用运算更复杂的逻辑。
- 一些厂商通过组合逻辑门生产实用,小型,集成的产品,如可编程逻辑器件。
-
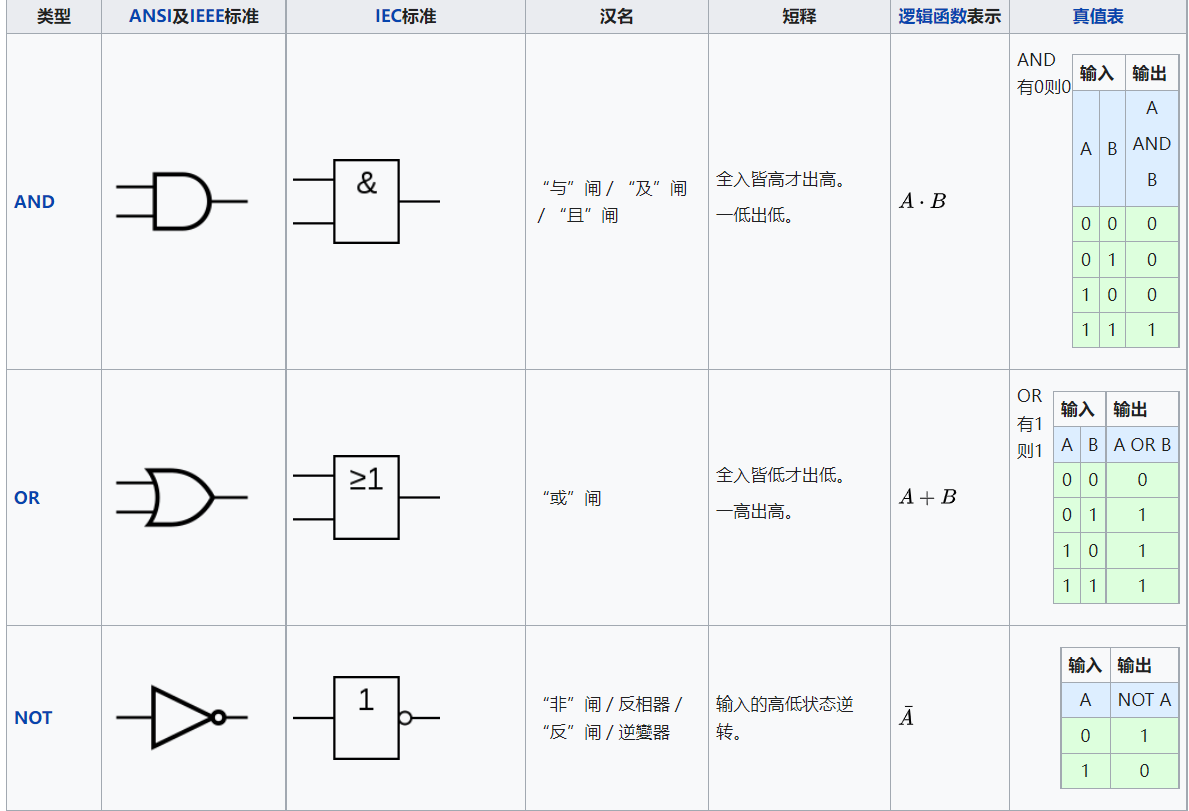
常用的逻辑门有两种常用表示
-
皆由ANSI(美国国家标准协会)/IEEE(电机电子工程师学会)Std 91-1984跟作为其补充的ANSI/IEEE Std 91a-1991。
-
“特殊形状符号”是用过去电路简图为基础以及50年代,60年代MIL-STD-806作衍生;
-
有时也描述成“军事”,而这个也反映了它的起源。
-
“IEC矩形国标符号”是以ANSI Y32.14跟一些早期工业用的符号为基础,再重新由IEEE跟IEC(国际电工委员会)做微调而成;在每个符号中皆可以发现有矩形的外框围着所代表的字,且相较于旧的表示法,他可以涵盖更多的逻辑门[1]。
-
ICE的标准也被转换成其他表示法,像是欧洲的EN(欧洲标准委员会)60617-12:1999,英国的BS(由英国标准学会制定) EN 60617-12:1999跟德国的DIN EN 60617-12:1998。
-
IEEE Std 91-1984跟IEC 60617-12的共同目标是提供一套有系统符号来描述复杂的逻辑功能跟数字电路。
- 这些逻辑的功能相较于AND闸和OR闸更加的复杂,例如中等大小的4比特计数器或大型的微处理器。
-
IEC 617-12以及接替他的IEC 60617-12没有很明确的标示出“特殊形状符号”,但是不可能不使用他们[1]。
-
然而在ANSI/IEEE 91和ANSI/IEEE 91a有提到:“根据IEC刊物第617期的第12部分指出特殊形状符号不会优先使用,但也没有和特殊形状符号有冲突”。
-
IEC 60617-12则包含了相应说明 :“即使非优先使用,使用其他由国家标准认可的符号-特殊形状符号,不应被认为和这个标准有冲突。
-
在使用其他特殊形状符号,以形成复数符号(例如使用如嵌入的符号)不应鼓励”。这项妥协方案使IEEE跟IEC协会遵守各自的标准。
-
第三种表示法较广泛用在欧洲,尤其是欧洲的学术界
-
在1980年代,示意图成为主要的方式用来设计印刷电路板以及客制化IC(例如逻辑阵列)。
- 而现在,客制化IC和现场可编程逻辑门阵列(field-programmable gate array)通常用Verilog或VHDL等硬件描述语言(Hardware Description Language;HDL)来设计。
-
与或非门
反相器和泡泡
- 在电子领域,NOT闸也常称反相器(Inverter)。
- 符号后圆圈常称泡泡,泡泡常用来表示外部逻辑状态及内部逻辑状态(气泡右侧及气泡左侧)的否定关系(1变0,0变1)。
- 电路图一定要定义0和1的状态,通常高电位=1 (=5V) , 低电位=0(=GND);
- 当然有些时候如果要将高电位设为0时,可以直接在电路图中说明,这称为直接极性指示,可参见IEEE Std 91/91A跟IEC 60617-12,
- 两者表示法中泡泡跟电路图中的说明可以在使用特殊形状符号及矩形国标符号的电路图中使用,但纯逻辑电路图只有泡泡可用。
与非/或非/异或

- XOR闸(exclusive-OR)的输出为1只有当两项输入是不同的状态;反之当两者输入相同,输出为0,不论输入为0或1。
- 如果有超过两项输入,当输入端为1的数目是奇数。
- 实际使用上,这些闸由更基本的逻辑门组合而成。
同或/是/蕴含/蕴含非

逻辑函数的表示方法及相互转换
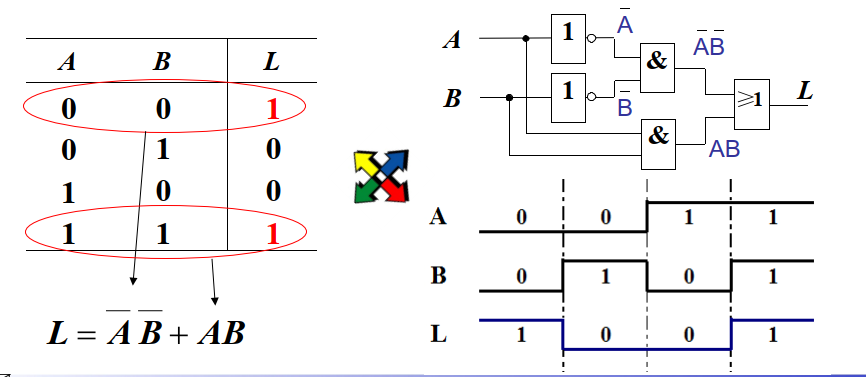
- 真值表:表征逻辑事件输入和输出之间全部可能状态的表格
- 逻辑代数式:用与,或,非等逻辑运算表示逻辑函数中各变量之间的逻辑关系
- 逻辑图:用与,或,非等逻辑符号表示逻辑函数中各变量之间的逻辑关系
- 波形图:不同输入信号作用下所对应的输出信号曲线表示电路的逻辑关系
逻辑表达式化简
基本公式
- 恒等式 1 恒等式2 0 − 1 律 A ⋅ 0 = 0 A + 1 = 1 自等律 A ⋅ 1 = A A + 0 = A 互补律 A ⋅ A ‾ = 0 A + A ‾ = 1 重叠律 A ⋅ A = A A + A = A 反演律 A B ‾ = A ‾ + B ‾ A + B ‾ = A ‾ ⋅ B ‾ 交换律 A ⋅ B = B ⋅ A A + B = B + A 结合律 A ⋅ ( B ⋅ C ) = ( A ⋅ B ) ⋅ C A + ( B + C ) = ( A + B ) + C 分配律 A ( B + C ) = A B + A C A + B C = ( A + B ) ( A + C ) 还原律 A ‾ ‾ = A ♣ \begin{array}{|c|c|c|} \hline & \text { 恒等式 } 1 & \text { 恒等式2 } \\ \hline \mathbf{0 - 1} \text { 律 } & {A} \cdot \mathbf{0}=\mathbf{0} & A+1=1 \\ \hline \text { 自等律 } & {A} \cdot \mathbf{1}= {A} & A+\mathbf{0}= {A} \\ \hline \text { 互补律 } & A \cdot \overline{A}=\mathbf{0} & A+\overline{A}=1 \\ \hline \text { 重叠律 } & {A} \cdot {A}= {A} & A+A=A \\ \hline \text { 反演律 } & \overline{A B}=\overline{A}+\overline{B} & \overline{A+B}=\overline{A} \cdot \overline{B} \\ \hline \text { 交换律 } & A \cdot B=B \cdot A & A+B=B+A \\ \hline \text { 结合律 } & A \cdot(B \cdot C)=(A \cdot B) \cdot C & A+(B+C)=(A+B)+C \\ \hline \text { 分配律 } & A(B+C)=A B+A C & A+B C=(A+B)(A+C) \\ \hline \text { 还原律 } & \overline{\overline{A}}=A &\clubsuit\\ \hline \end{array} 0−1 律 自等律 互补律 重叠律 反演律 交换律 结合律 分配律 还原律 恒等式 1A⋅0=0A⋅1=AA⋅A=0A⋅A=AAB=A+BA⋅B=B⋅AA⋅(B⋅C)=(A⋅B)⋅CA(B+C)=AB+ACA=A 恒等式2 A+1=1A+0=AA+A=1A+A=AA+B=A⋅BA+B=B+AA+(B+C)=(A+B)+CA+BC=(A+B)(A+C)♣
异或和同或的常用运算公式
-
F = A ⊕ B F = A ⊙ B A ⊕ 0 = A A ⊙ 1 = A A ⊕ 1 = A ˉ A ⊙ 0 = A ˉ A ⊕ A = 0 A ⊙ A = 1 A ⊕ A ˉ = 1 A ⊙ A ˉ = 0 A ⊕ B ˉ = A ⊕ B ‾ = A ⊕ B ⊕ 1 A ⊙ B ˉ = A ⊙ B ‾ = A ⊙ B ⊙ 0 A ⊕ B = B ⊕ A A ⊙ B = B ⊙ A A ⊕ ( B ⊕ C ) = ( A ⊕ B ) ⊕ C A ⊙ ( B ⊙ C ) = ( A ⊙ B ) ⊙ C A ( B ⊕ C ) = A B ⊕ A C A + ( B ⊙ C ) = ( A + B ) ⊙ ( A + C ) \begin{array}{|l|l|} \hline {F=A \oplus B} & {F=A \odot B} \\ \hline A \oplus 0=A & A \odot 1=A \\ \hline A \oplus 1=\bar{A} & A \odot 0=\bar{A} \\ \hline A \oplus A=0 & A \odot A=1 \\ \hline A \oplus \bar{A}=1 & A \odot \bar{A}=0 \\ \hline A \oplus \bar{B}=\overline{A \oplus B}=A \oplus B \oplus 1 & A \odot \bar{B}=\overline{A \odot B}=A \odot B \odot 0 \\ \hline A \oplus B=B \oplus A & A \odot B=B \odot A \\ \hline A \oplus(B \oplus C)=(A \oplus B) \oplus C & A \odot(B \odot C)=(A \odot B) \odot C \\ \hline A(B \oplus C)=A B \oplus A C & A+(B \odot C)=(A+B) \odot(A+C) \\ \hline \end{array} F=A⊕BA⊕0=AA⊕1=AˉA⊕A=0A⊕Aˉ=1A⊕Bˉ=A⊕B=A⊕B⊕1A⊕B=B⊕AA⊕(B⊕C)=(A⊕B)⊕CA(B⊕C)=AB⊕ACF=A⊙BA⊙1=AA⊙0=AˉA⊙A=1A⊙Aˉ=0A⊙Bˉ=A⊙B=A⊙B⊙0A⊙B=B⊙AA⊙(B⊙C)=(A⊙B)⊙CA+(B⊙C)=(A+B)⊙(A+C)
-
调换律:
若 A ⊕ B = C , 则 必 有 A ⊕ C = B , B ⊕ C = A ; 若 A ⊙ B = C , 则 必 有 A ⊙ C = B , B ⊙ C = A . 若 {A} \oplus \mathrm{B}=\mathrm{C} , 则必有 {A} \oplus \mathrm{C}= {B}, {B} \oplus \mathrm{C}= {A} ; \\ 若 {A} \odot B=\mathrm{C} , 则必有 {A} \odot \mathrm{C}=\mathrm{B}, {B} \odot \mathrm{C}= {A} . 若A⊕B=C,则必有A⊕C=B,B⊕C=A;若A⊙B=C,则必有A⊙C=B,B⊙C=A.