1. 创建一棵简单的二叉树

本篇文章重点讲解关于二叉树的几种遍历，所以手动创建一棵二叉树举例子。

1.1 二叉树结构体实现

typedef int data_type; //把数据类型typedef一下，方便随时更换数据类型

typedef struct BTreeNode
{
	data_type x;     //结点要存储的数据
	struct BTreeNode* left;  //二叉树的左孩子
	struct BTreeNode* right;  // 二叉树的右孩子
}Node;

1.2 创造一个二叉树结点的函数

本篇文章我们要手动创建一棵二叉树来举例子，所以写一个函数方便创造结点，结点创建好后，我们手动连接结点，就可形成二叉树。

Node* buyNode(data_type a) //传入结点的数据
{
	Node* node = (Node*)malloc(sizeof(Node)); //创造一个结点
	if (node == NULL) //养成好习惯，判断是否malloc成功
	{
		perror("malloc:");
		exit(-1);
	}
	node->x = a; // 结点的值
	node->left = node->right = NULL; // 结点的左孩子和右孩子都为空
	return node; //返回这个结点
}

1.3 手动创造一棵二叉树

    Node* n1 = buyNode(1); //1是该结点的值，以此类推
	Node* n2 = buyNode(2);
	Node* n3 = buyNode(3);
	Node* n4 = buyNode(4);
	Node* n5 = buyNode(5);
	Node* n6 = buyNode(6);
	Node* n7 = buyNode(7);

	n1->left = n2;  //手动连接，结点n1的左孩子是 n2
	n1->right = n3; // 结点n1的右孩子是 n3
	n2->left = n4; // 结点n2的左孩子是 n4
	n2->right = n5; //结点n2的右孩子是 n5
	n3->left = n6;  //结点n3的左孩子是 n6
	n4->left = n7;  //结点n4的左孩子是 n7

创建的二叉树逻辑图如下：

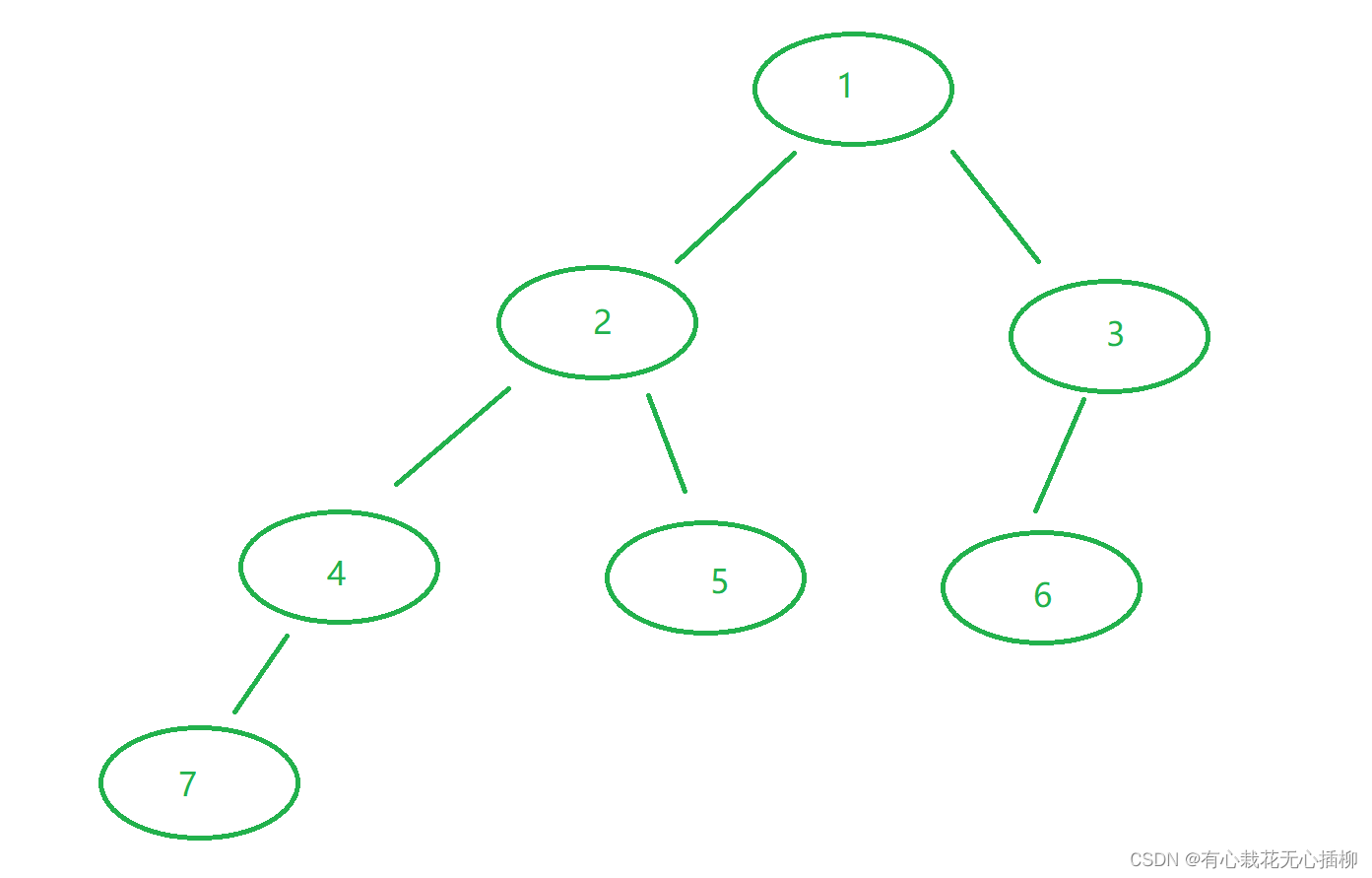
我们的二叉树就创建好了，接下来开始用这颗二叉树讲解我们的几种遍历
（实际上创建二叉树并不是这样创建的）

2.为什么要遍历？

我们先来点知识的铺垫：

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前,前序遍历又叫深度优先遍历（根-左-右）
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。(左-根-右)
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。（左-右-根）

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

3.最重要的知识：由二叉树引出的子问题分析

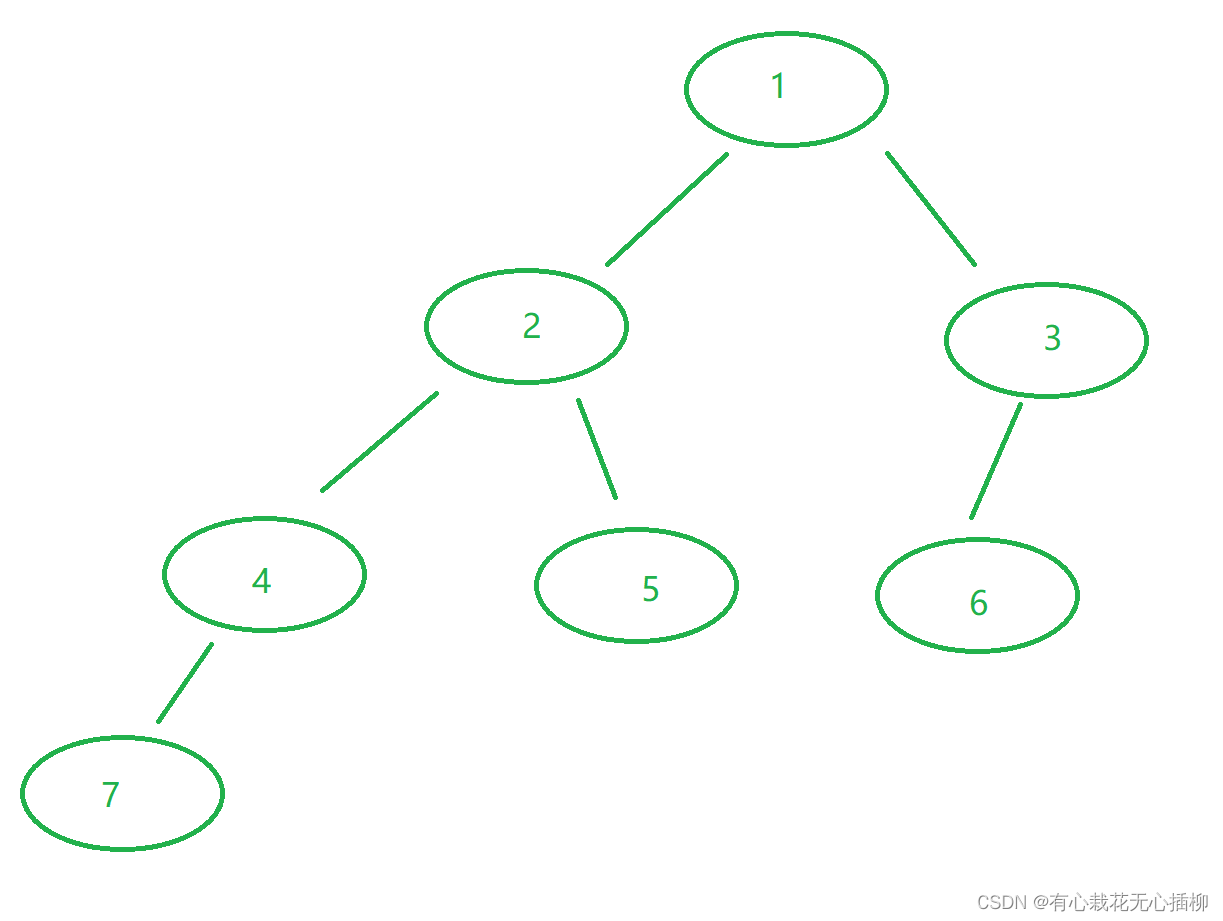
为什么二叉树这么好用，引出了各种各样的二叉树。
主要是二叉树可以把一个大树分为一棵课子树，让一棵棵子树去解决问题，最终大树的问题得到解决。
也就说，二叉树把一个问题，转化成了规模更小的子问题，子问题解决了，我们最终的问题也就解决了。这是一个非常重要的思想，算法里随处可见。

注意：二叉树里规模最小的问题是 NULL，而不是最后一个结点。
最后一个结点的子问题是NULL，NULL不可再被分解。

也就是说，我们上图中，实际应该是这样的。

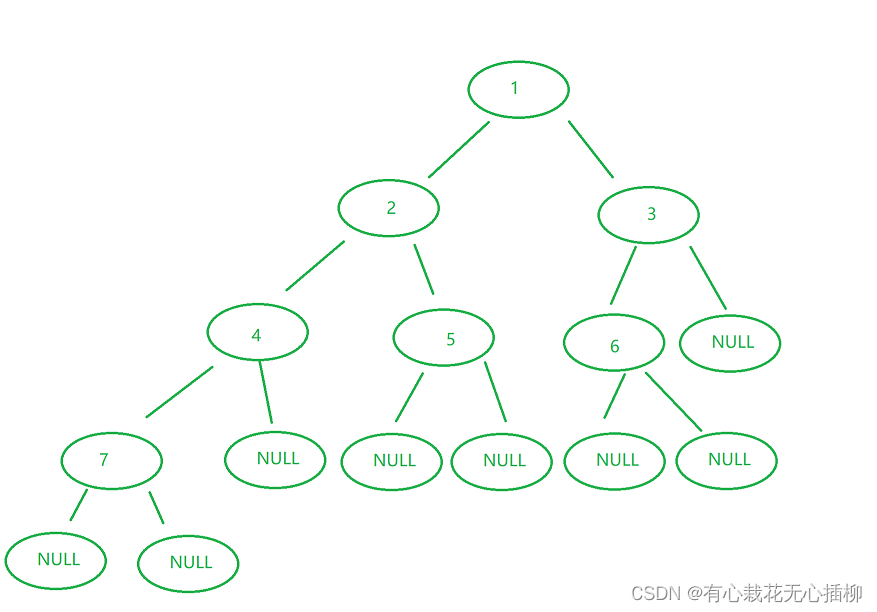
这点非常重要 切记！！！

4.遍历

4.1 前序遍历

前序遍历就是 先打印根，再打印左子树和右子树。也就是（根-左-右）
注意是，左子树和右子树，子树还能再被分成更小的子树。
先看代码

void preOrder(Node* root)
{
	if (root == NULL) // 如果遇到NULL就直接return返回
	{
	    printf("NULL "); //不打印NULL也可以，我们这里打印，显示最真实的结构
		return;
	}
	printf("%d ", root->x);//遇到根结点就打印
	preOrder(root->left);//递归进左子树
	preOrder(root->right);//递归进右子树
}

preOrder(n1);
//1 2 4 7 NULL NULL NULL 5 NULL NULL 3 6 NULL NULL NULL

来画个图感受一下

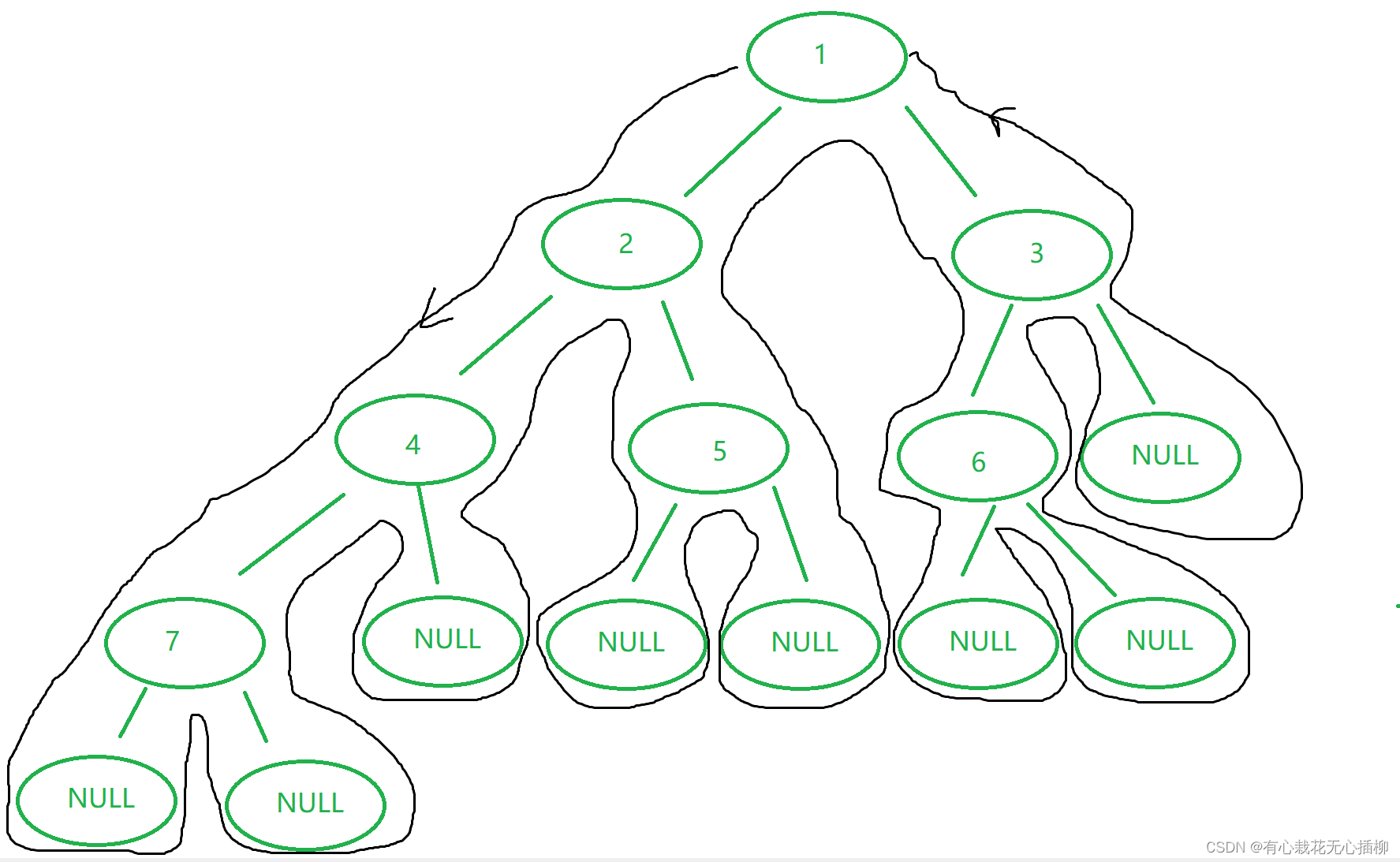
整个过程就形成了这个看起来像大树根一样的图
这就是前序遍历，也叫深度优先遍历。
别小看这个过程，这个过程利用递归，完成了从深入到回溯的过程，遍历了整棵树。其思想是以深度为优先，就是每次先走到最底层，走不下来再返回来，走另外一条路。

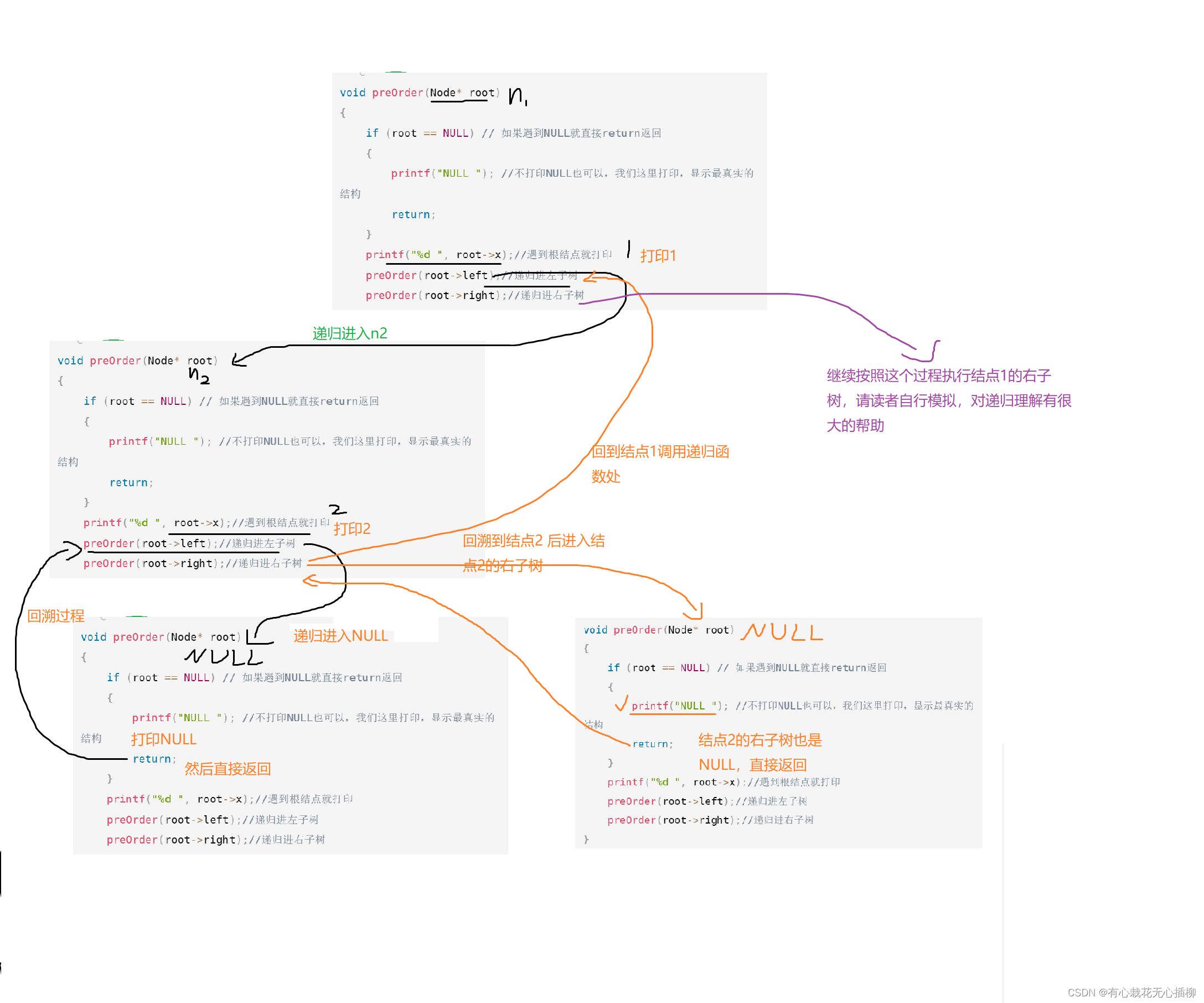
接下来以代码模拟一下，以下图可能很长，耐心看一下，自己也可以手动像我这样模拟一下，对理解递归有很大的帮助。
因为上面那个图画起来步骤太烦琐，我们这里举这么一棵树模拟一下
这棵树打印结果是：
1 2 NULL NULL 3 NULL NULL

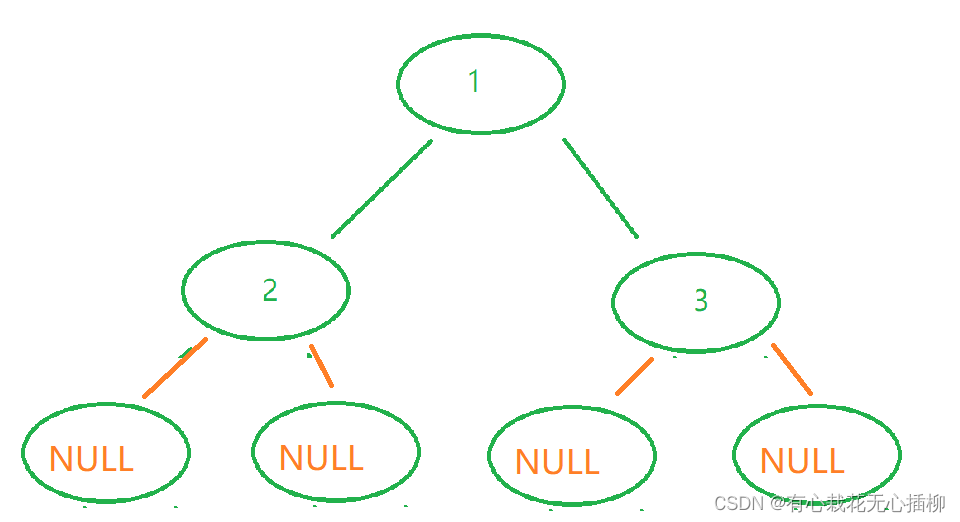
首先，先解决每一棵左子树，到达NULL后回溯

然后回溯到结点2后，继续递归进入结点2右子树，右子树也是NULL，直接返回，此时结点2的函数执行完成，直接回到n1调用处

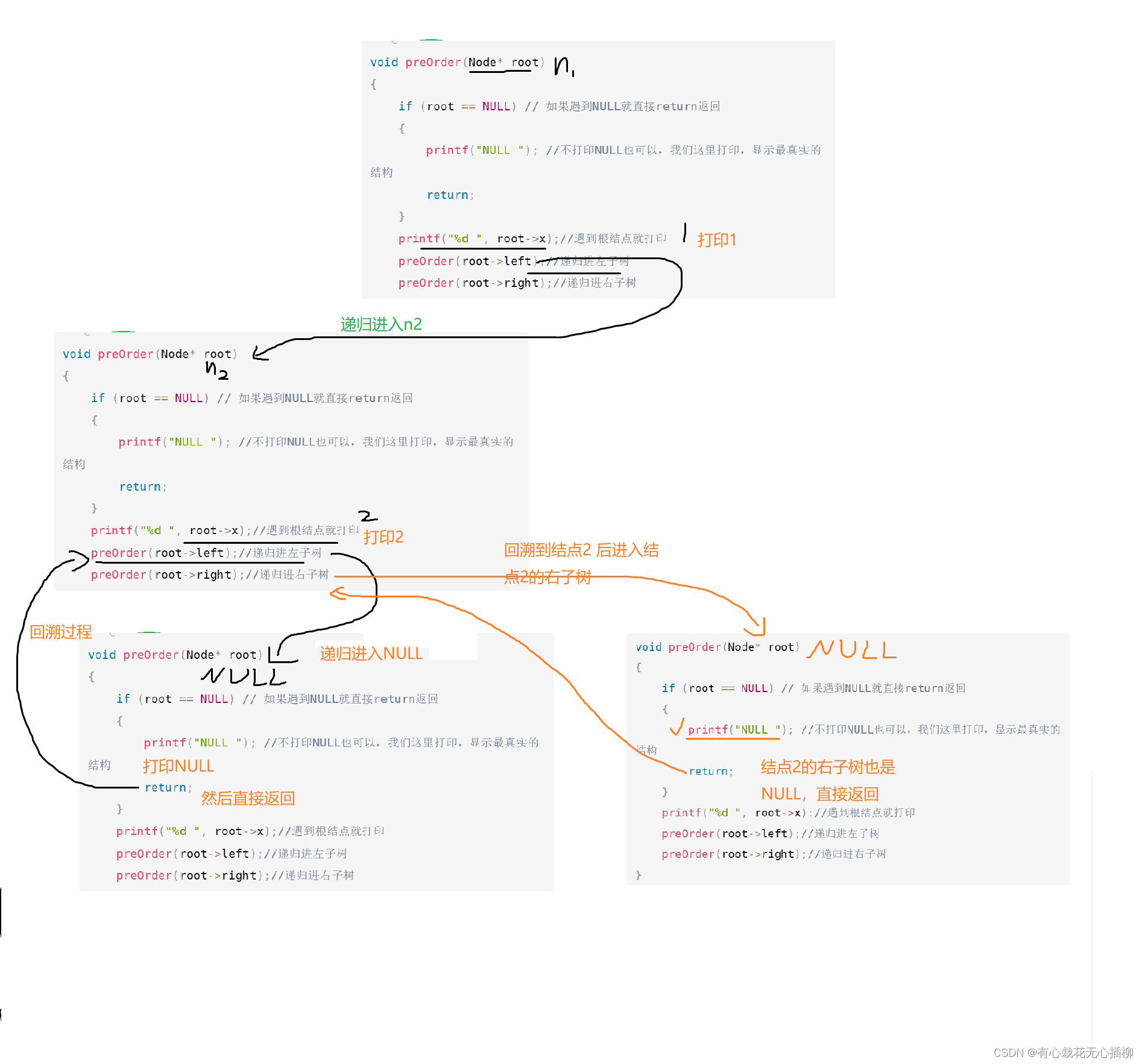
到这里为止打印了 1 2 NULL NULL，1的右子树交给读者去自行模拟一下吧~

4.2 中序遍历

中序遍历就是先打印左子树，再打印根，再打印右子树（也就是左-根-右）
整个过程和前序遍历一样可以自行模拟一下。
答案是7 4 2 5 1 6 3 (未打印NULL的情况)

void inOrder(Node* root)
{
	if (root == NULL)
	{
		return;
	}
	inOrder(root->left);
	printf("%d ", root->x);
	inOrder(root->right);
}

4.3 后序遍历

后序遍历就是先打印左子树，再打印右子树，再打印根（也就是左-右-根）
整个过程和前序遍历一样，可以自行模拟一下。
答案是 7 4 5 2 6 3 1 （为打印NULL的情况）

void postOrder(Node* root)
{
	if (root == NULL)
	{
		return;
	}
	postOrder(root->left);
	postOrder(root->right);
	printf("%d ", root->x);
}

5.总结

其实由代码我们可以发现一个规律，printf这个函数位置的规律。
想打印前序遍历，就放在进入左子树和右子树递归前。
想打印中序遍历，就放在中间。
想打印后序遍历，就放在最后。
这个确实是一个很好记忆方法，不过更重要的是知道它的本质。