0 简介

论文题目：Selection bias mitigation in recommender system using uninteresting items based on temporal visibility
发表情况：2023年，Expert Systems With Applications
论文地址：https://doi.org/10.1016/j.eswa.2022.118932
论文源代码：目前没发现

1 动机

这篇论文应该是借鉴了“Told You I Didn’t Like It”: Exploiting Uninteresting Items for Effective Collaborative Filtering的想法，我们主要关注是这两篇论文的不同之处。

主要区别在于计算使用前偏好上：

• Told You I Didn’t Like It：利用矩阵分解，只考虑用户评分因素；
• Selection bias mitigation：结合用户活动、商品受欢迎程度和时间因素，综合衡量商品对用户的可见性，并使用时间可见性（temporal visibility）对缺失数据进行非均匀加权，以计算他们的使用前偏好。

2 主要方案

2.1 使用前偏好分析

• 使用前偏好一般基于用户对物品外部特征的偏好，这些特征可以在没有实际使用的情况下获得，如电影类型、主演等。
• 使用后偏好取决于用户对物品内部特征的偏好，比如电影故事情节。

对于使用前偏好较低的物品，用户在看到它们时不会进行交互。可以推断，他们的使用后偏好很低，即评分很低。

对于用户评分的物品，可以简单地推断出他们的使用前偏好非常高。挑战在于如何准确地推断未评分物品的使用前偏好。这是一类（one-class）问题(Pan et al.， 2008)，也就是说，观察到的评分是正样本，缺乏负样本。当隐性反馈缺乏负样本时，已有研究提出了两种应对策略。一种是基于样本的学习(He & McAuley, 2016)，从缺失数据中提取负样本。另一种是全数据学习(whole-data-based learning)，将所有缺失的数据视为负样本，并赋予其权重，作为它们是负样本的置信度。前者不需要考虑所有缺失数据，效率高，但不可避免地存在丢失有价值信息的风险，模型的鲁棒性较差。后者使用所有数据，覆盖率较高，但效率较低。为了保持模型的鲁棒性，我们使用了基于全数据的学习。加权正则化矩阵分解(WRMF)将所有缺失数据作为负样本，并分配小的统一权重(Hu, Koren & Volinsky, 2008)。我们认为未评分项目的置信度与负样本相同，但这与实际情况不一致。基于项目的受欢迎程度，元素替代最小二乘(eALS)对未评分的项目进行非均匀加权(He, Zhang, Kan & Chua, 2016)。越受欢迎的商品，在用户不互动的情况下，越容易被用户看到，负样本的置信度越高，应给予更高的权重。但是，这些方法没有考虑到用户之间的差异以及时间因素对知名度的影响。

目前的大多数方法都是基于一种体验，即只看不互动的项目显示了用户的负面偏好。一个物品越有可能被用户看到，而用户不进行交互，那么它是一个负面例子的置信度就越高。关键是如何准确地推断用户是否看到了该项目。目前流行的方法是利用商品的受欢迎程度来推断商品对用户的可见性，但可靠性不高。事实上，不同活动的用户对物品的可见性不同，物品的受欢迎程度随着时间的推移而变化(He et al.， 2014)。我们将提出一种更细粒度的加权方案。同时，为了缓解整体数据学习带来的效率问题，我们使用eALS对目标算法进行优化。该方法为处理加权矩阵分解以优化元素级参数提供了一种新的思路。该方法避免了传统ALS矩阵分解中需要矩阵求逆的问题，提高了效率。

2.2 ITV-eALS模型

评过分的项目使用前偏好为1：
$$p_{ui}=\{\begin{array}{l}0,r_{ui}=\text{ null }\\ 1,r_{ui}\ne \text{ null }\end{array}$$
利用矩阵分解来预测
$$J=\sum _{u=1}^m\sum _{i=1}^n{w}_{ui}{\left(p_{ui-}{\hat{r}}_{ui}\right)}^2+\lambda \left(\sum _{u=1}^m{\Vert x_u\Vert }^2+\sum _{i=1}^n{\Vert y_i\Vert }^2\right)$$
此处${\hat{r}}_{ui}=x_u{y}_i^T$，$W={\left(w_{ui}\right)}_{m\times n}$。
本文和“Told You I Didn’t Like It” 最大区别就在于$W$的计算，“Told You I Didn’t Like It” 在计算$W$的时候只考虑用户评分项目的数量，本文不但考虑用户评分项目的数量（通过${\hat{\alpha }}_u$来体现），还加入了时间因素，某个时间阶段用户评分项目的数量
$$w_{ui}=\{\begin{array}{c}1,p_{ui}=1\\ \epsilon {\hat{\alpha }}_u+(1-\epsilon ){\hat{\beta }}_i,p_{ui}=0\end{array}$$
${\hat{\alpha }}_u={\sum }_{i=1}^n{p}_{ui}$表示用户$u$在某一个时间阶段$[t_{min},t_{max}]$评分项目的数量，并利用$\log$函数归一化：
$${\hat{\alpha }}_u=\frac{\log \left({\alpha }_u\right)}{\max (\log (\alpha ))}$$
${\hat{\beta }}_i={\sum }_{u=1}^m{p}_{ui}$表示项目$i$在某一个时间阶段$[t_{min},t_{max}]$被用户评分的数量，并利用$\log$函数归一化：
$${\hat{\beta }}_i=\frac{\log \left({\beta }_i\right)}{\max (\log (\beta ))}$$
后面的填充方法和“Told You I Didn’t Like It” 一样。

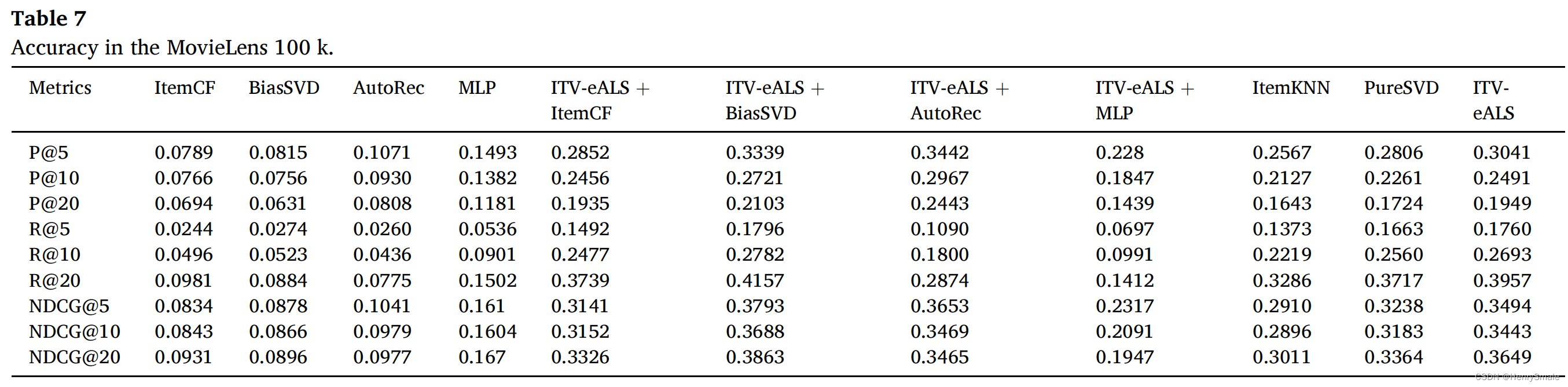
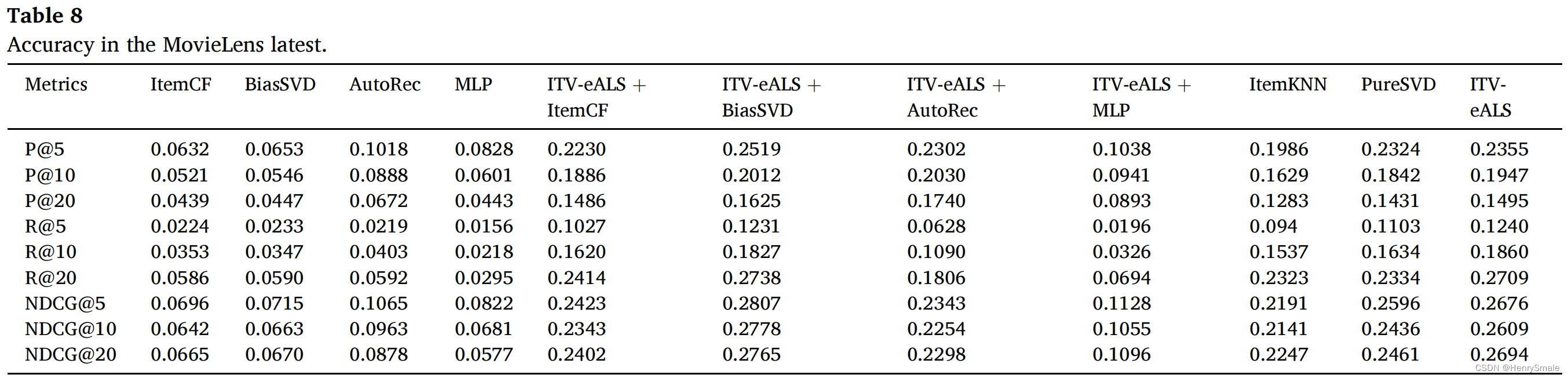
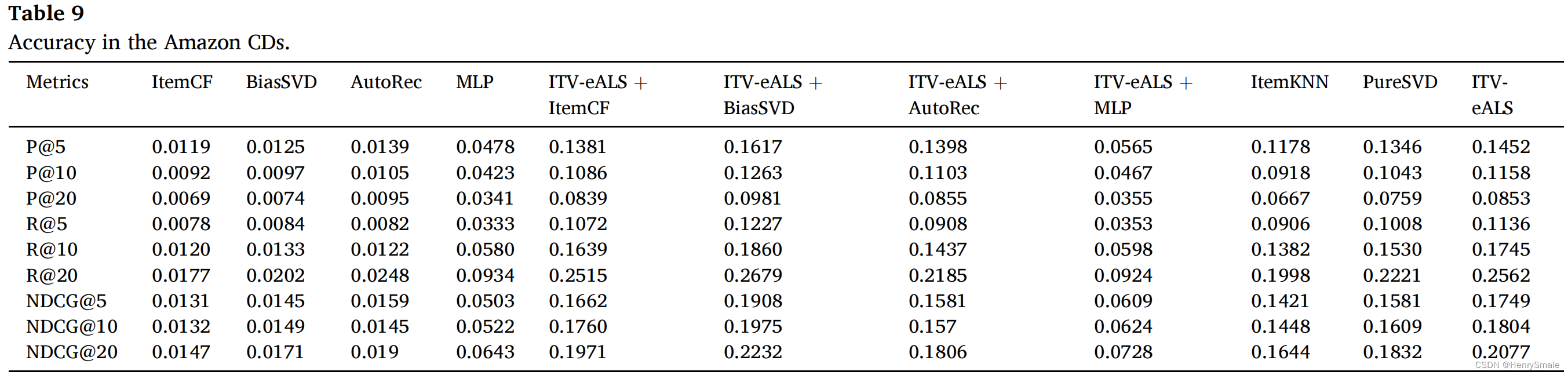
3 实验结果