核心思想

  本文提出一种基于图神经网络的图匹配方法，首先利用节点相似度构建初始的匹配关系，然后利用局部的一致性对初始的匹配关系进行迭代优化，不断筛除误匹配点，得到最终的匹配结果。本文还提出几种措施来降低计算复杂度，以实现较大规模的图匹配任务。

实现过程

  首先给出基本的概念和符号定义，图$G=(V,A.X,E)$，$V$表示节点集合，$A$表示关联矩阵，$X$表示节点特征矩阵，$E$表示边特征矩阵，$G_s,G_t$分别表示用于匹配的源图和目标图，$S$表示对应关系矩阵。根据本文对图匹配问题的定义，目标是寻找最优的$S$，使得下述目标函数取得最大值

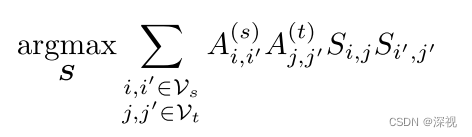
$N_T(i)$表示与节点$i$之间的距离小于等于$T$的邻域，称之为T-hop邻域。而邻域（局部）一致性是指，对于一对匹配点$i,j$，他们1-hop邻域$N_1(i)$内的所有点都是匹配点。

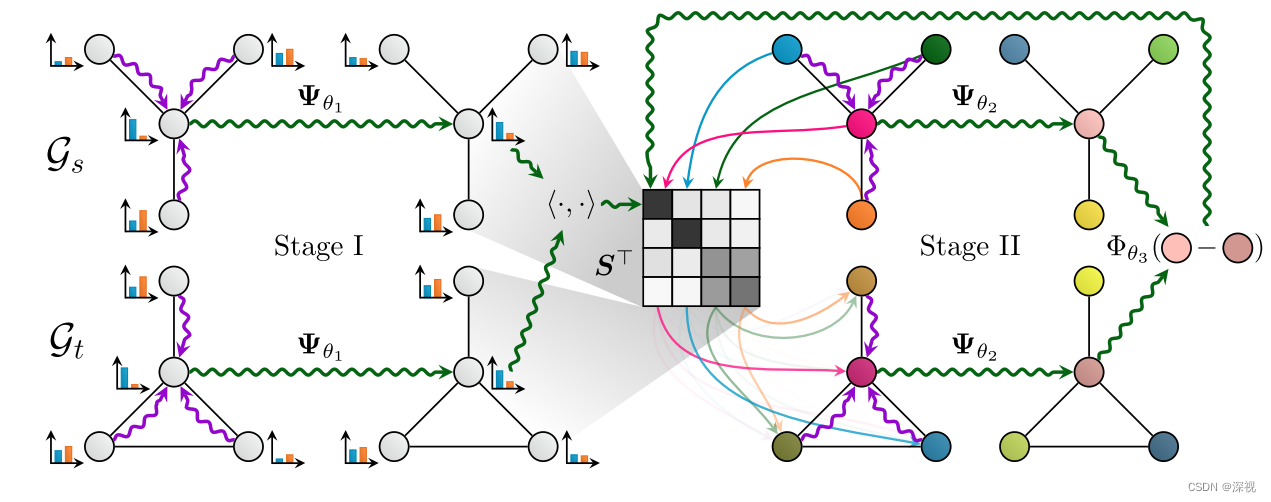
  如上图所示，算法分成两个阶段：第一阶段根据节点特征之间的相似度得到初始的对应关系矩阵$S^{(0)}$；第二阶段利用局部一致性约束进行迭代优化得到最终的对应关系矩阵$S^{(L)}$。第一阶段，作者称之为局部特征匹配，利用共享权重的图神经网络${\Psi }_{{\theta }_1}$分别提取两个图$G_s,G_t$的深度节点特征$H_s,H_t$。然后利用下式得到初始的对应关系矩阵$S^{(0)}$

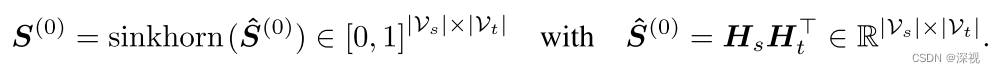
设真实的匹配关系为${\pi }_{gt}(\cdot )$，则第一阶段的损失函数为

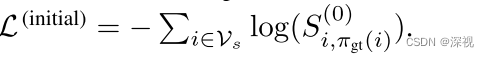
  对应关系矩阵$S^{(0)}$实质上是一个从源图的节点函数空间$L(G_s)$到目标图节点函数空间$L(G_t)$的一个映射，因此可得

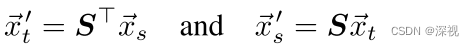
其中

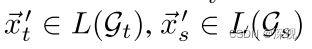
  以单位矩阵$I_{|V_s|}$的形式构建源图的节点指示函数，利用对应关系矩阵$S^{(l)}$可以将其从源图$G_s$映射到目标图$G_t$。然后利用图神经网络${\Psi }_{{\theta }_2}$向邻域内其他的节点传递信息，如下式

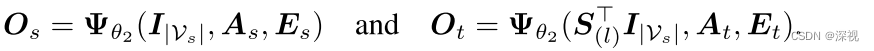
这样每个节点上都聚合了邻域内其他顶点的信息，通过计算聚合后节点特征之间的差异${\vec{d}}_{i,j}={\vec{o}}_i^{(s)}-{\vec{o}}_j^{(t)}$，就可以计算节点对$(i,j)$之间的邻域一致性，差异越小表示一致性越强。将差异${\vec{d}}_{i,j}$通过一个多层感知机${\Phi }_{{\theta }_3}$映射后，用于优化对应关系矩阵

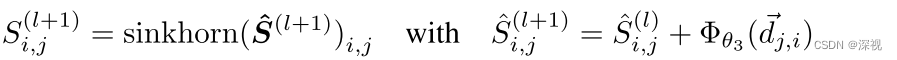
上述优化过程可以反复进行，迭代$L$次。最终的损失函数如下

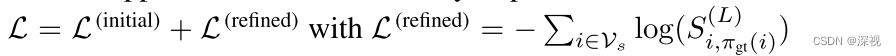
  为了将上述匹配过程应用到大规模的匹配点集中，作者提出了几点改进措施：

1. 稀疏匹配。通过将初始对应关系矩阵$S^{(0)}$中，匹配得分较低的点滤除，仅保留匹配得分最高的$K$个对应点，可以使$S^{(0)}$变得更加稀疏。
2. 更换节点指示函数。尽管单位矩阵$I_{|V_s|}$计算十分高效，但参数的复杂度较高。可以使用随机采样的节点函数$R_s^{(l)}\sim N(0,1)$来取代节点指示矩阵。
3. Softmax规范化。sinkhorn函数计算不够高效，且容易出现梯度消失的问题，可以使用逐行的softmax来取代sinkhorn函数。
4. 迭代次数。相比于训练阶段，测试阶段可以使用更少的迭代次数。

创新点

• 提出一种两阶段的基于图神经网络的图匹配方法
• 针对大规模点集匹配问题，提出了优化措施

算法总结

  本文是基于深度学习，尤其是基于图神经网络解决图匹配问题的代表性文章。二阶段逐步迭代优化的方式，其实与传统图像处理中实现特征点匹配的思想非常接近。局部一致性限制了算法的求解规模，缓解了图匹配问题随着节点数量增长，计算量爆炸的问题。