前言:算法训练系列是做《代码随想录》一刷,个人的学习笔记和详细的解题思路,总共会有60篇博客来记录,记录结构上分为 思路,代码实现,复杂度分析,思考和收获,四个方面。如果这个系列的博客可以帮助到读者,就是我最大的开心啦,一起LeetCode一起进步呀;)
目录
LeetCode93.复原IP地址
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考与收获
Leetcode. 78 子集
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考与收获
Leetcode90.子集II
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考与收获
LeetCode93.复原IP地址
链接:93. 复原 IP 地址 - 力扣(LeetCode)
1. 思路
做这道题目之前,最好先把**131.分割回文串 (opens new window)**这个做了。
这道题目相信大家刚看的时候,应该会一脸茫然。其实只要意识到这是切割问题,切割问题就可以使用回溯搜索法把所有可能性搜出来,然后根据题意进行一些合法性的判断,和刚做过的**131.分割回文串 (opens new window)**就十分类似了。切割问题可以抽象为树型结构,如图:
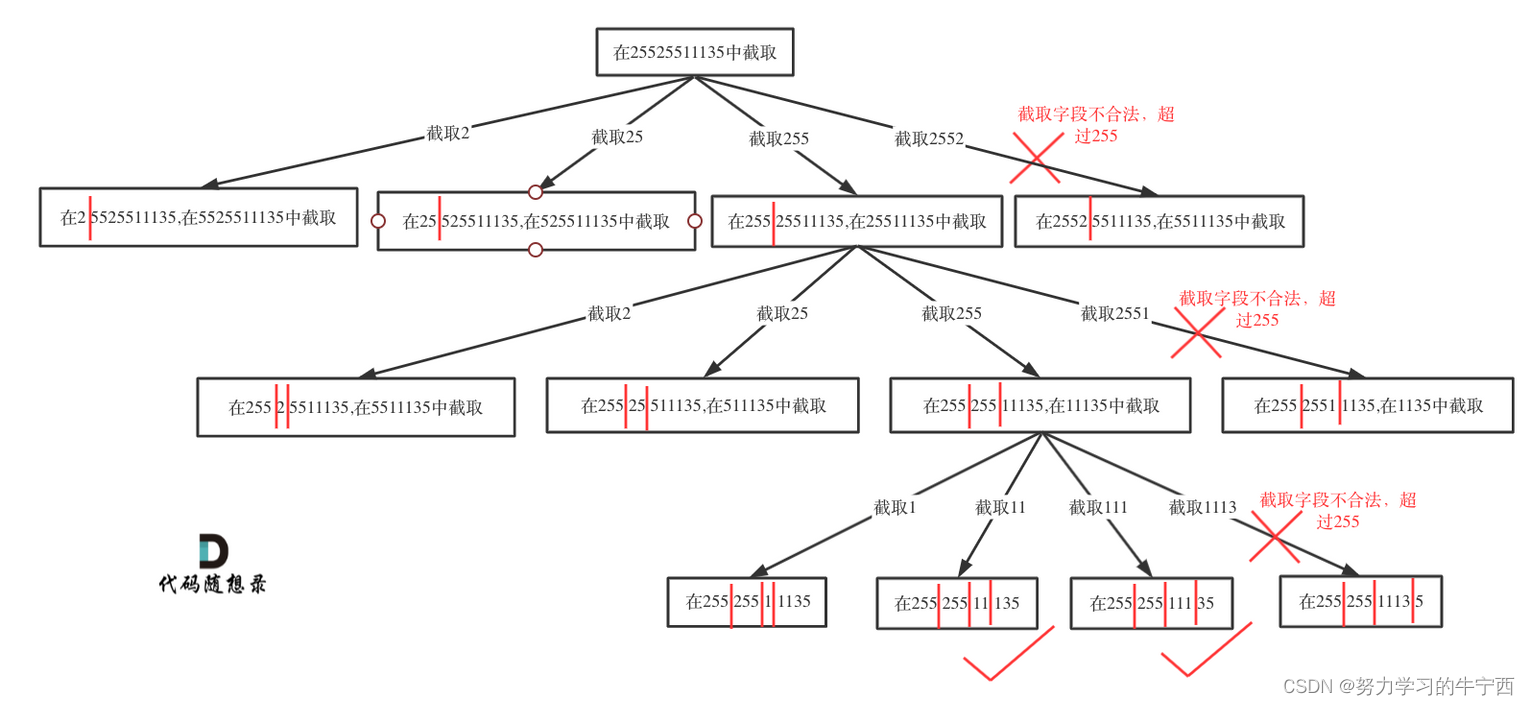
2. 代码实现
2.1 递归参数
在**131.分割回文串 (opens new window)**中我们就提到切割问题类似组合问题。
startIndex一定是需要的,因为不能重复分割,记录下一层递归分割的起始位置;本题我们还需要一个变量pointNum,记录添加逗点的数量。
所以代码如下:
# python3
class Solution:
def __init__(self):
self.result = []
def restoreIpAddresses(self, s: str) -> List[str]:
'''
本质切割问题使用回溯搜索法,本题只能切割三次,所以纵向递归总共四层
因为不能重复分割,所以需要start_index来记录下一层递归分割的起始位置
添加变量point_num来记录逗号的数量[0,3]
'''
self.result.clear()
if len(s) > 12: return []
self.backtracking(s, 0, 0)
return self.result
def backtracking(self, s: str, start_index: int, point_num: int) -> None:
2.2 递归终止条件
终止条件和**131.分割回文串 (opens new window)**情况就不同了,本题明确要求只会分成4段,所以不能用切割线切到最后作为终止条件,而是分割的段数作为终止条件;
pointNum表示逗点数量,pointNum为3说明字符串分成了4段了,然后验证一下第四段是否合法,如果合法就加入到结果集里;
# python3
def backtracking(self, s: str, start_index: int, point_num: int) -> None:
# Base Case
if point_num == 3:
if self.is_valid(s, start_index, len(s)-1):
self.result.append(s[:])
return
2.3 单层搜索的逻辑
在**131.分割回文串 (opens new window)**中已经讲过在循环遍历中如何截取子串;
在for (int i = startIndex; i < s.size(); i++)循环中 [startIndex, i] 这个区间就是截取的子串,需要判断这个子串是否合法。如果合法就在字符串后面加上符号.表示已经分割,如果不合法就结束本层循环,如图中剪掉的分支:
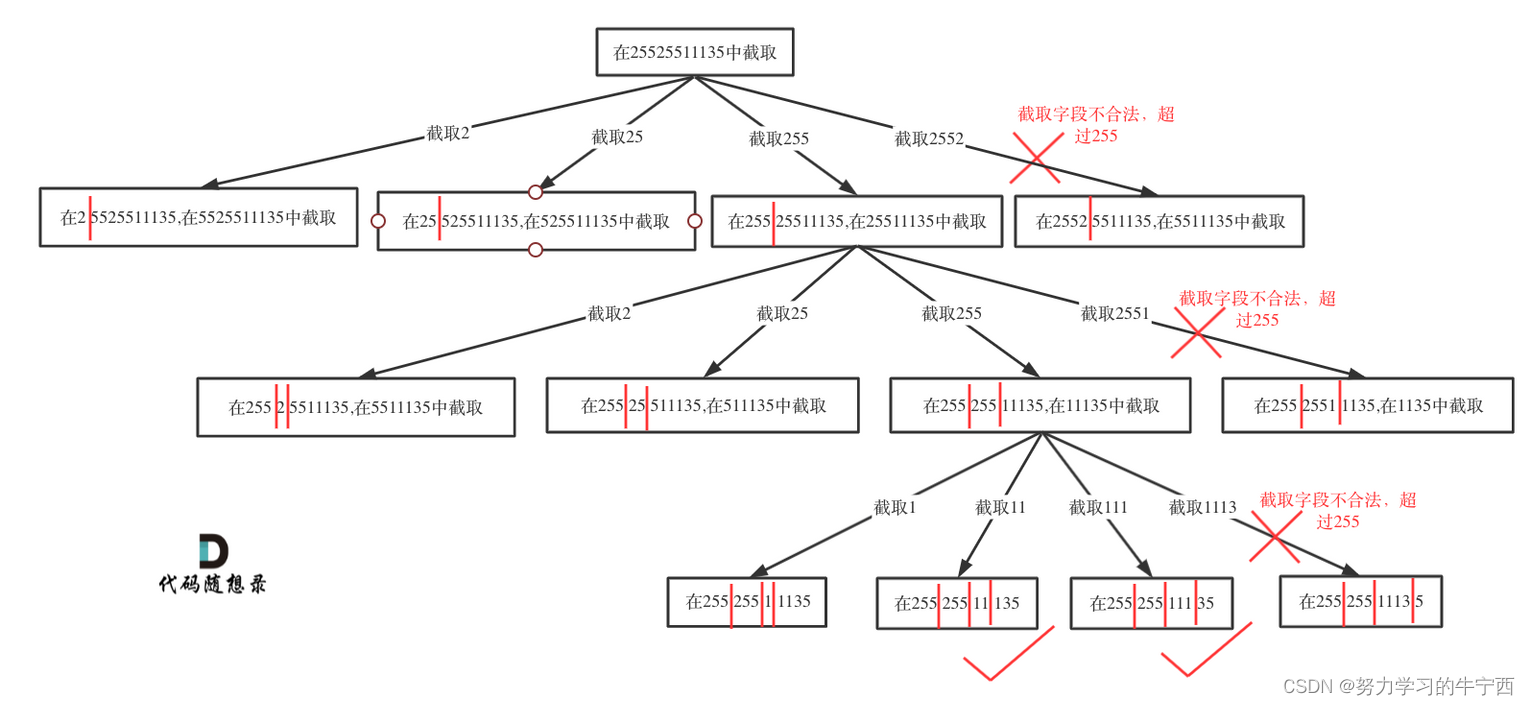
然后就是递归和回溯的过程:
递归调用时,下一层递归的startIndex要从i+2开始(因为需要在字符串中加入了分隔符.),同时记录分割符的数量pointNum 要 +1。
回溯的时候,就将刚刚加入的分隔符. 删掉就可以了,pointNum也要-1。
# python3
# 单层递归逻辑
for i in range(start_index, len(s)):
# [start_index, i]就是被截取的子串
if self.is_valid(s, start_index, i):
s = s[:i+1] + '.' + s[i+1:]
self.backtracking(s, i+2, point_num+1)
# 在填入.后,下一子串起始后移2位
s = s[:i+1] + s[i+2:] # 回溯
else:
# 若当前被截取的子串大于255或者大于三位数,直接结束本层循环
break
2.4 判断子串是否合法
最后就是在写一个判断段位是否是有效段位了。
主要考虑到如下三点:
- 段位以0为开头的数字不合法
- 段位里有非正整数字符不合法
- 段位如果大于255了不合法
代码如下:
def is_valid(self, s: str, start: int, end: int) -> bool:
if start > end: return False
# 若数字是0开头,不合法
if s[start] == '0' and start != end:
return False
if not 0 <= int(s[start:end+1]) <= 255:
return False
return True
2.5 总体代码如下
class Solution:
def __init__(self):
self.result = []
def restoreIpAddresses(self, s: str) -> List[str]:
'''
本质切割问题使用回溯搜索法,本题只能切割三次,所以纵向递归总共四层
因为不能重复分割,所以需要start_index来记录下一层递归分割的起始位置
添加变量point_num来记录逗号的数量[0,3]
'''
self.result.clear()
if len(s) > 12: return []
self.backtracking(s, 0, 0)
return self.result
def backtracking(self, s: str, start_index: int, point_num: int) -> None:
# Base Case
if point_num == 3:
if self.is_valid(s, start_index, len(s)-1):
self.result.append(s[:])
return
# 单层递归逻辑
for i in range(start_index, len(s)):
# [start_index, i]就是被截取的子串
if self.is_valid(s, start_index, i):
s = s[:i+1] + '.' + s[i+1:]
self.backtracking(s, i+2, point_num+1) # 在填入.后,下一子串起始后移2位
s = s[:i+1] + s[i+2:] # 回溯
else:
# 若当前被截取的子串大于255或者大于三位数,直接结束本层循环
break
def is_valid(self, s: str, start: int, end: int) -> bool:
if start > end: return False
# 若数字是0开头,不合法
if s[start] == '0' and start != end:
return False
if not 0 <= int(s[start:end+1]) <= 255:
return False
return True
3. 复杂度分析
(我自己这样子分析的,正确性有待考究)
-
时间复杂度:O(2^N)
因为每一个元素的状态无外乎割与不割,所以时间复杂度为O(2^n)
-
空间复杂度:O(1)
本题递归深度最多为4,递归栈所用空间为常数级别,result和path都是全局变量,传的都是引用,不会有额外申请新的空间;
4. 思考与收获
- 在**131.分割回文串 (opens new window)中我列举的分割字符串的难点,本题都覆盖了。而且本题还需要操作字符串添加逗号作为分隔符,并验证区间的合法性。可以说是131.分割回文串 (opens new window)**的加强版;
- 关键是按照流程依次解决各个难点问题,思路清晰。
Reference: 代码随想录 (programmercarl.com)
本题学习时间:90分钟。
Leetcode. 78 子集
链接:78. 子集 - 力扣(LeetCode)
1. 思路
求子集问题和**77.组合 (opens new window)和131.分割回文串 (opens new window)**又不一样了。
子集问题 vs 组合问题分割问题
如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!
其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。那么既然是无序,取过的元素不会重复取,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!
什么时候for可以从0开始呢?
求排列问题的时候,就要从0开始,因为集合是有序的,{1, 2} 和{2, 1}是两个集合,排列问题后续就会讲到的。
以示例中nums = [1,2,3]为例把求子集抽象为树型结构,如下:
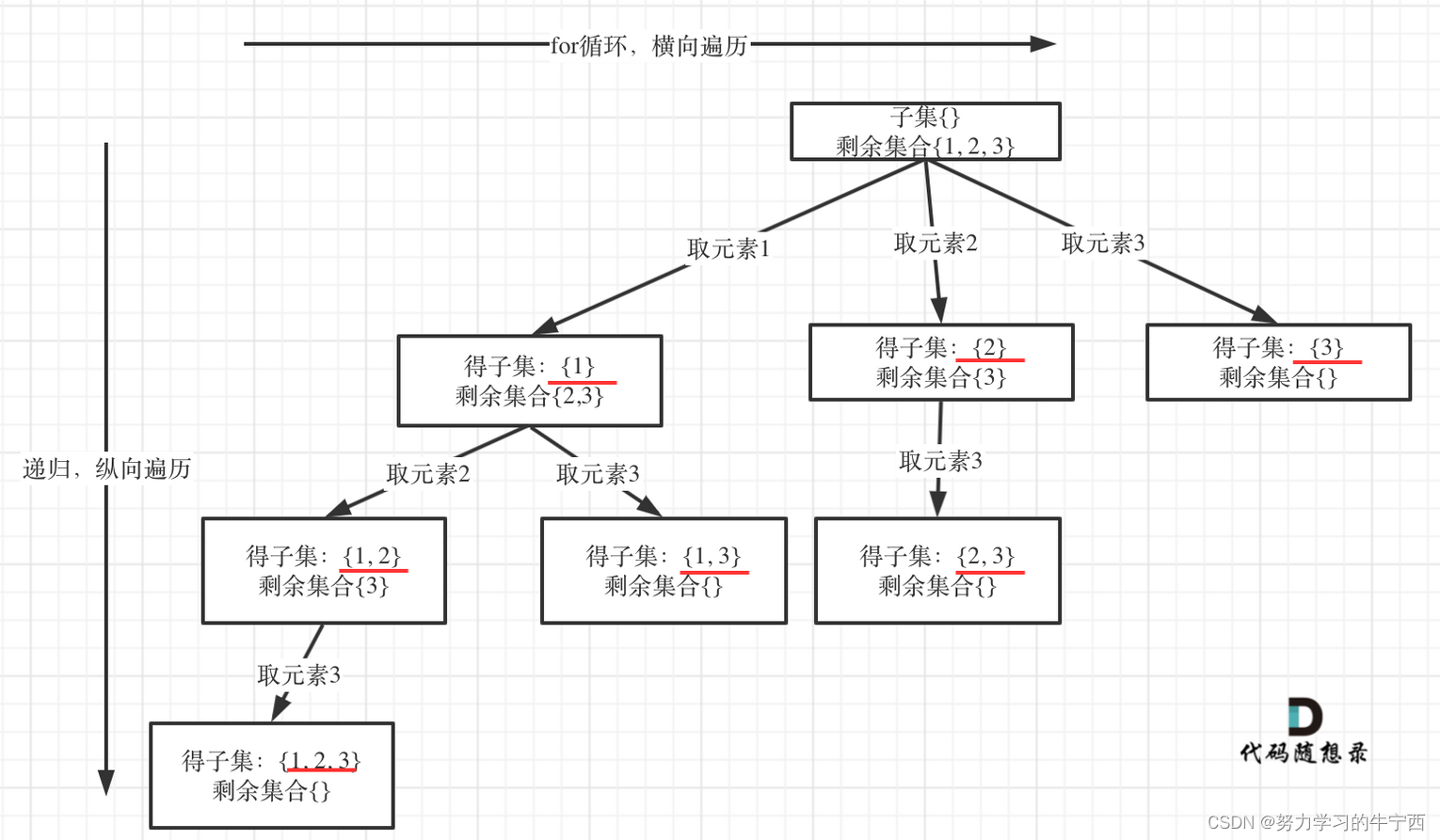
从图中红线部分,可以看出遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合。
2. 代码实现
2.1 递归函数参数
全局变量数组path为子集收集元素,二维数组result存放子集组合。(也可以放到递归函数参数里);递归函数参数在上面讲到了,需要startIndex。
class Solution:
def __init__(self):
self.path: List[int] = []
self.paths: List[List[int]] = []
def subsets(self, nums: List[int]) -> List[List[int]]:
self.paths.clear()
self.path.clear()
self.backtracking(nums, 0)
return self.paths
def backtracking(self, nums: List[int], start_index: int) -> None:
2.2 递归终止条件
从图中可以看出:
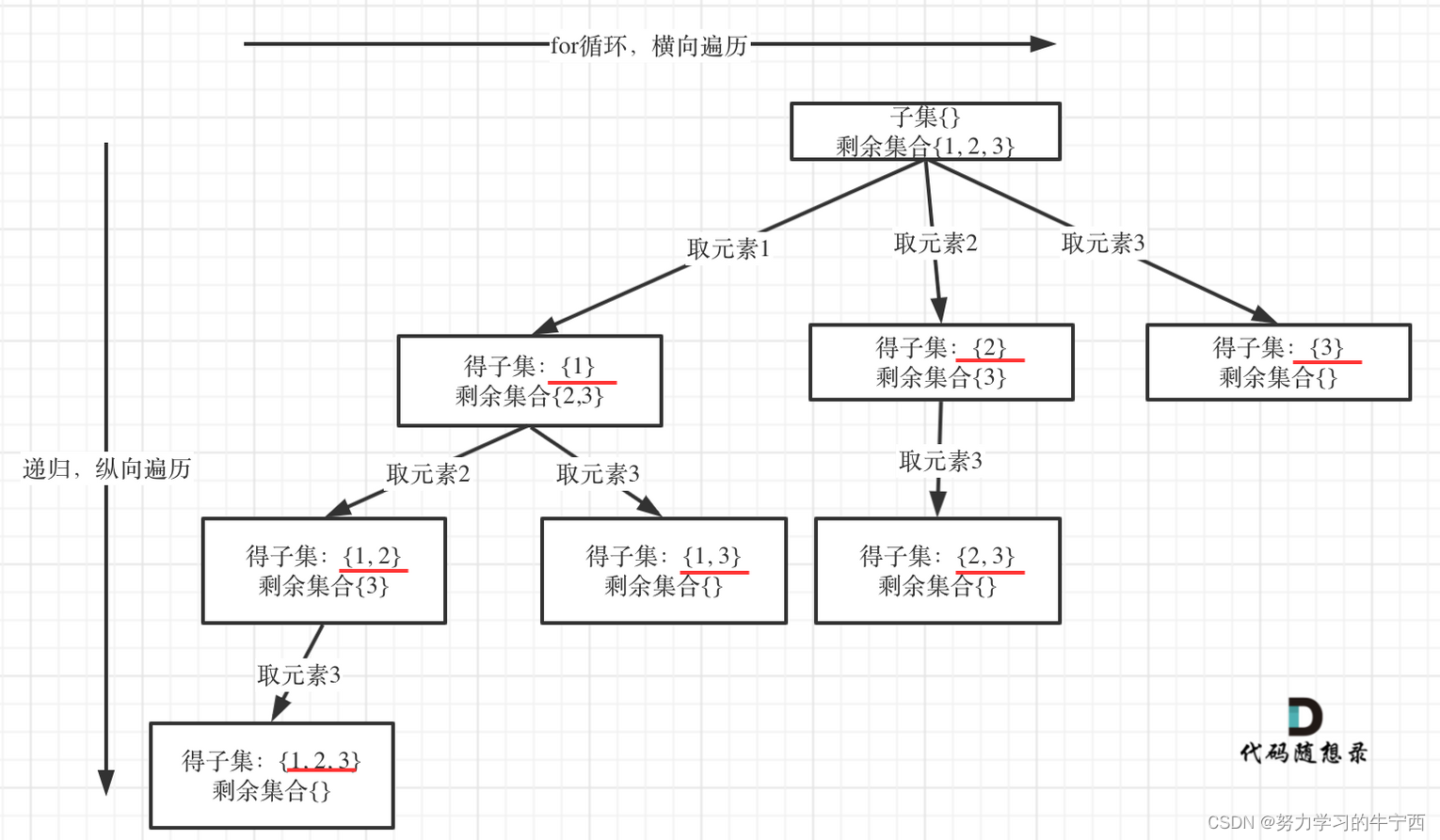
剩余集合为空的时候,就是叶子节点。
那么什么时候剩余集合为空呢?就是startIndex已经大于数组的长度了,就终止了,因为没有元素可取了,代码如下:
def backtracking(self, nums: List[int], start_index: int) -> None:
# Base Case
if start_index == len(nums):
return
💡 其实可以不需要加终止条件,因为下面for循环的条件,startIndex >= nums.size(),本层for循环本来也结束了
2.3 单层搜索逻辑
求取子集问题,不需要任何剪枝!因为子集就是要遍历整棵树。
那么单层递归逻辑代码如下:
# 单层递归逻辑
for i in range(start_index, len(nums)):
self.path.append(nums[i])
self.backtracking(nums, i+1)
self.path.pop() # 回溯
2.4 整体代码
# 回溯算法 子集问题
# time:O(2^N);space:O(N)
class Solution(object):
# 定义好全局变量
def __init__(self):
self.path = []
self.result = []
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
if nums == []: return [[]]
self.backtracking(nums,0)
return self.result
def backtracking(self,nums,startIndex):
# 收集结果要在终止条件前面,不然会错过叶子节点的值
self.result.append(self.path[:])
# 终止条件
if startIndex > len(nums)-1:
return
# 单层循环逻辑
for i in range(startIndex,len(nums)):
self.path.append(nums[i])
self.backtracking(nums,i+1)
self.path.pop()
3. 复杂度分析
-
时间复杂度:O(2^n)
因为每一个元素的状态无外乎取与不取,所以时间复杂度为O(2^n)
-
空间复杂度:O(n)
递归深度为n,所以系统栈所用空间为O(n),每一层递归所用的空间都是常数级别,注意代码里的result和path都是全局变量,就算是放在参数里,传的也是引用,并不会新申请内存空间,最终空间复杂度为O(n)
4. 思考与收获
- 子集问题整体来说并不难,但是要清楚子集问题和组合问题、分割问题的的区别,子集是收集树形结构中树的所有节点的结果,而组合问题、分割问题是收集树形结构中叶子节点的结果;
- startIndex的作用和组合问题以及切割问题中都是一样的,保证剩余元素进入下一层递归的时候,都是从当前元素的后面一个开始取的,否则会有1,2和2,1的重复出现;
- 其实终止条件是可以不写的,因为for循环中starIndex≥ len(nums)的时候根本也不会进入for loop ,可能担心不写终止条件会不会无限递归?并不会,因为每次递归的下一层就是从i+1开始的;
- 本题的集合问题也是没有任何剪枝操作的,因为我们本来就要遍历整棵树,然后收集树上每个节点的集合;
- 收集子集的代码必须放在终止条件的上面,不然会错过叶子节点的子集情况。
Reference: 代码随想录 (programmercarl.com)
本题学习时间:60分钟。
Leetcode90.子集II
链接:90. 子集 II - 力扣(LeetCode)
1. 思路
这道题目和**78.子集 (opens new window)**区别就是集合里有重复元素了,而且求取的子集要去重。
那么关于回溯算法中的去重问题,在40.组合总和II (opens new window)中已经详细讲解过了,和本题是一个套路。剧透一下,后期要讲解的排列问题里去重也是这个套路,所以理解“树层去重”和“树枝去重”非常重要。
用示例中的[1, 2, 2] 来举例,如图所示: (注意去重需要先对集合排序)
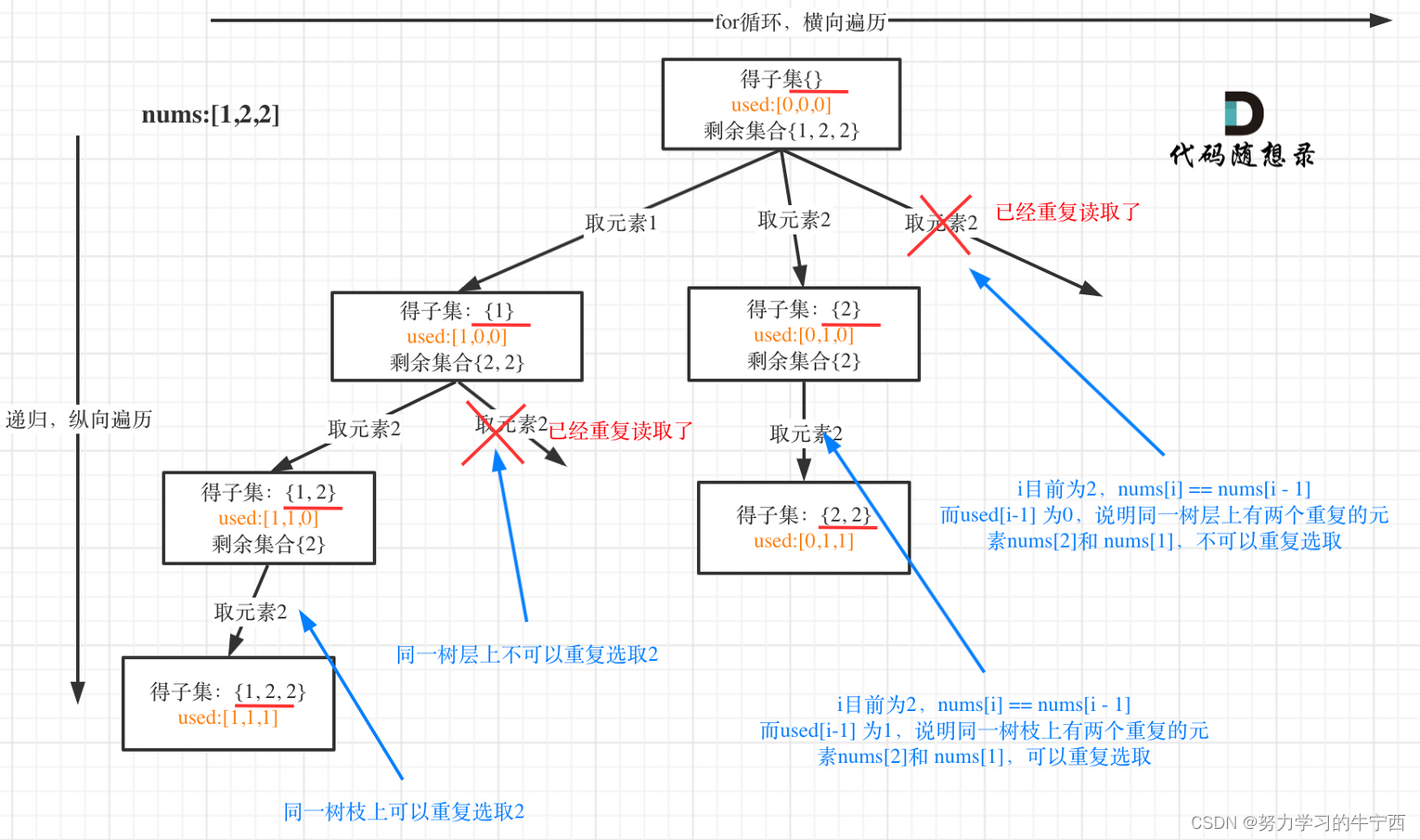
从图中可以看出,同一树层上重复取2 就要过滤掉,同一树枝上就可以重复取2,因为同一树枝上元素的集合才是唯一子集!
2. 代码实现
# 回溯算法 子集问题
# time:O(2^N);space:O(N)
class Solution(object):
# 定义全局变量
def __init__(self):
self.path = []
self.result = []
def subsetsWithDup(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
# 排序 time:O(NlogN)
nums.sort()
if nums == []: return [[]]
self.backtracking(nums,0,[0]*len(nums))
return self.result
def backtracking(self,nums,startIndex,used):
# 收集结果,每个节点都收集
self.result.append(self.path[:])
# 递归终止条件
if startIndex > len(nums)-1:
return
# 单层递归逻辑
for i in range(startIndex,len(nums)):
# 去重逻辑
if i>0 and nums[i] == nums[i-1] and used[i-1] == 0:
continue
self.path.append(nums[i])
used[i] = 1
self.backtracking(nums,i+1,used)
self.path.pop()
used[i] = 0
3. 复杂度分析
-
时间复杂度:O(2^n)
因为每一个元素的状态无外乎取与不取,所以时间复杂度为O(2^n)
-
空间复杂度:O(n)
递归深度为n,所以系统栈所用空间为O(n),每一层递归所用的空间都是常数级别,注意代码里的result和path都是全局变量,就算是放在参数里,传的也是引用,并不会新申请内存空间,最终空间复杂度为O(n)
4. 思考与收获
- 本题就是组合总和II + 子集,把里面的知识点综合运用一下,没有新的知识点;
- 本题其实也可以不通过used数组去重,但是这种方法更好理解更通用,之后的排列问题中还要用到的,所以掌握这一种就可以;
- 本题的终止条件实际上可以省略,因为startIndex≥ len(nums) 之后已经不可以进入for loop了;
Reference: 代码随想录 (programmercarl.com)
本题学习时间:60分钟。
本篇学习时间为3个多小时,总结字数为6000+;针对回溯算法中的切割问题和子集问题做了相应的练习,切割问题本质上也是一种组合问题,子集问题与前两者的区别是,子集问题收集所有节点上的数值。(求推荐!)