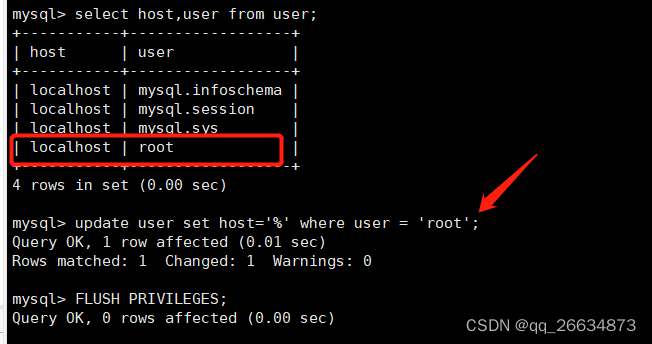
A simple pendulum studied using Hall effect sensor and Arduino

利用霍尔效应传感器和Arduino研究了一个简单的钟摆：原文（Hall effect sensor (scitation.org)）

ARTICLES YOU MAY BE INTERESTED IN

• Measurement of gravitational acceleration using Arduino and rotating fluid

• Developing physics teaching material Newton’s law based on local wisdom: Plait

• Developing physics learning tools based on the local community traditionabout global warming to improve student’s understanding

A Simple Pendulum Studied Using Hall Effect Sensor and Arduino

利用霍尔效应传感器和Arduino研究了一个简单的钟摆

Abstract. An experiment has been conducted to investigate oscillation motion on simple pendulum system by using Hall effect sensor and arduino. The hardware for experiment used were push button, Hall effect sensor, arduino, LCD display, indicator lamp, and power supply. Meanwhile the software used were C code program by using IDE ardunio compiler. Mechanic device used were stative scaffolder, rope, magnetic ball, digital scales, and ruler. The experiment is aimed at investigating the effect of rope length, mass of object, and oscillation angle toward the period and frequency of oscillation as well as to measure acceleration of gravitation. The result showed that the acceleration of gravitation gained was 9.87 ± 0.06 m/s2 with percentage of error reached 0.71% if compared to the theoretic value. The result also showed that oscillation period was equal with the length root of rope, meanwhile oscillation frequency was equal with one per length root of rope. Besides that, the result also proof that mass of object and oscillation angle was not influential toward period and frequency of oscillation on simple pendulum system.

摘要：利用霍尔效应传感器和arduino对单摆系统的振荡运动进行了实验研究。实验使用的硬件有按键、霍尔传感器、arduino、液晶显示器、指示灯、电源。软件采用的是C代码程序，采用IDE ardunio编译器。机械装置有支架、绳索、磁球、数字秤、尺等。实验研究了绳索长度、物体质量和摆动角度对摆动周期和频率的影响

INTRODUCTION

Hands on activity is a learning approach that involves students to dig for concepts through hands activities. Hands on-based learning process attracts students to interest in learning and encourages students to learn about basic concepts of physics and the implementation in daily life [1]. Implementation of hands on approach in learning process can be done through experimental method. Learning activities through experiment assist students to actively involved in comprehending basic concepts of physics and their implementation. In addition, physics experiment helps to form a scientific attitude and sharpen skill. It involves students to do observation, draw hypothesis and answer questions, analyze, and interpret data, summarize, and communicate the result [2]. Physics experiment requires learning media such as props/measurement tools in measuring physics quantity as well as collecting data.

动手活动是一种让学生通过动手活动来挖掘概念的学习方法。动手学习过程吸引学生的学习兴趣，鼓励学生学习物理的基本概念，并在日常生活中实现[1]。实践方法在学习过程中可以通过实验方法来实现。通过实验的学习活动，帮助学生积极参与物理基本概念的理解和实践。此外，物理实验有助于形成科学态度和磨练技能。它涉及学生进行观察，提出假设和回答问题，分析和解释数据，总结和交流结果[2]。物理实验在测量物理量和收集数据时，需要学习道具/测量工具等媒介。

The use of props in learning process creates interesting teaching and learning process and makes physics concepts to be more real that makes them easy to be learned [3]. Props are also important in experimental activity as tools to visualize physics phenomena, to measure, collect data and train science process skill of students [4]. Using props in learning process gives opportunity for students to build knowledge through investigation process. Besides, props also helpful in which helping students to actively participate in learning, conduct experiment freely, help students to be creative and answer students eagerness to know about something [5]. One of physics phenomenon that requires props in learning is oscillation motion on simple pendulum.

在学习过程中使用道具，创造了有趣的教学和学习过程，使物理概念更真实，更容易学习。在实验活动中，道具作为可视化物理现象、测量、收集数据和训练学生科学过程技能的工具也很重要。在学习过程中使用道具，让学生有机会在探究的过程中构建知识。此外，道具也很有帮助，帮助学生积极参与学习，自由进行实验，帮助学生发挥创造力，回答学生的求知欲。单摆上的振荡运动是学习中需要道具的物理现象之一。

Simple pendulum is needed as a helpful tool to visualize oscillation motion and instrument to measure physics parameter like period and frequency. Physics quantity in simple harmonic motion in the case of simple pendulum can be determined through measuring oscillation time. Generally, time measurement is done by using stopwatch and operated using hand. This method can cause uncertainty of significant measurement toward the result of counting. Therefore, more appropriate and accurate instrument is required to measure oscillation time [6]. Timer tape trickster and photogate timer are considered as an accurate time measurement tool compared to stopwatch. However, it needs more expensive that causes difficulty for teachers and students to get [7, 8]. The solution is using other electronic tools

简单的摆作为振荡运动的可视化工具和测量周期、频率等物理参数的仪器是需要的。在单摆情况下，可以通过测量振荡时间来确定简谐运动的物理量。一般来说，时间的测量是用秒表完成的，用手操作。这种方法对计数结果有显著的不确定性。因此，需要更合适、更精确的仪器来测量振荡时间[6]。与秒表相比，计时器和光栅计时器被认为是一种精确的时间测量工具。然而，它需要更昂贵的，造成教师和学生难以获得[7,8]。解决办法是使用其他电子工具

which are cheap and easy to get that helps developing effective and efficient props. Sensor and arduino are the effective and cheaper props to develop kinds of measurement tools for laboratory [9, 10, 11].

The mixture between sensor and arduino in physics experiment improves measurement quality toward physics quantities and acquisition of data can be done according to the real time [2]. Sensor and arduino are also used as simple, effective, sensitive and efficient measurement tools to overcome precision and accuracy of low measurement [12]. The other advantage of using sensor and arduino as experimental props is that they are automatic, avoiding human error, and producing accurate measurement result [13]. The advantages of physics experiments based on sensor and arduino namely: sharpen algorithmic thinking skill, skill to collect data, and solving problem [11]. Besides that, supports STEM-based learning process by combining physics, instrumentation electronics, math, computer programming that improve students’ interest and motivation [1, 9, 14].

这是便宜和容易获得的，有助于开发有效和高效的道具。Sensor和arduino是开发各种实验室测量工具的有效和廉价的道具[9,10,11]。
在物理实验中，传感器与arduino混合使用，提高了对物理量的测量质量，可以实时[2]进行数据采集。传感器和arduino作为简单、有效、灵敏、高效的测量工具，克服了测量[12]精度低的问题。使用传感器和arduino作为实验道具的另一个好处是，它们是自动的，避免了人为误差，产生了精确的测量结果[13]。基于传感器和arduino的物理实验的优势在于:提高算法思维能力，收集数据的能力，解决问题[11]的能力。此外，通过结合物理学、仪器电子学、数学、计算机编程来支持基于stem的学习过程，提高学生的兴趣和动机[1,9,14]。

THEORITICAL BACKGROUND

An object system with simple harmonic motion is a particle that regularly moves periodically toward a point of balance. The important characteristics of simple harmonic motion are period and frequency. Period is defined as the time required for oscillation and frequency is defined as the quantity of oscillation that obtained every second. If the quantity of oscillation of an object is signaled with n and the time needed for oscillation is t, the mathematically the frequency of oscillation is signaled as follows:

具有简谐运动的物体系统是一个粒子有规律地周期性地向平衡点运动。简谐运动的重要特性是周期和频率。周期被定义为振荡所需的时间，频率被定义为每秒钟获得的振荡量。如果用n对一个物体的振荡量进行信号，振荡所需时间为t，则从数学上对振荡频率进行定义:
$$T=\frac{t}{n}\dots \dots \dots \dots （1）$$

in which T is the period in second (s). Relation between the quantity of oscillation and time for frequency is signaled using:

其中T为周期，单位为秒(s)。振荡量与频率时间之间的关系用:
$$f=\frac{n}{t}\dots \dots \dots \dots （2）$$

where f is the frequency in hertz (Hz). While, relation between period and frequency is signaled by equation:

其中f是频率的赫兹(Hz)。而周期与频率的关系由式表示:
$$T=\frac{1}{f}\dots \dots \dots \dots （3）$$

A simple pendulum is formed from a small object hanged up on a slight rope. Assuming that there is no mass of the rope and can be relatively neglected on the pendulum. Simple pendulum will move back and forth with neglected friction such as the simple harmonic motion. The pendulum will move in a constant track with similar amplitude of point of balance in both sides and when moving through the point of balance, the pendulum will experience maximum speed. Oscillation motion of a pendulum with its forces is shown in Fig. 1 as the following.

一个简单的钟摆是由一个小物体挂在一根细绳上形成的。假设绳子没有质量，在摆上可以相对忽略。单摆在忽略摩擦力的情况下来回运动，如单谐运动。钟摆在匀速轨道上运动，其两侧平衡点的振幅相似，当钟摆运动过平衡点时，其速度达到最大值。摆随力的振荡运动如图1所示。

FIGURE 1. Simple pendulum system with its working forces.

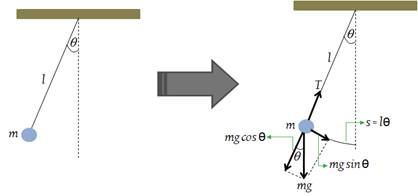
The movement of pendulum along the arch is written by s = lq, in which q is the angle made by rope toward vertical direction (the balance line) and l is the length of rope. If the restoring force is equal with s or q, the movement will be simply harmonic motion. The restoring force is the total force on the pendulum which is equal with weight (mg) that contacts with the arch.

摆沿弧的运动记为s = lθ，其中θ为绳子与垂直方向(平衡线)的夹角，l为绳子的长度。如果恢复力等于s或θ，则运动为简谐运动。恢复力是作用在钟摆上的总力，等于与弧接触的重量(mg)。
$$F=-mg\sin (\theta )\dots \dots \dots \dots (4)$$
In which g is the earth’s gravitational acceleration. The negative sign in equation 4 shows the direction of F force against the angle movement of q. Because F is equal with sin(q) and not for the q itself, therefore the movement is not simply harmonic motion (GHS). However, if q is small, then sin(q) is almost equal with q when the angle is revealed in radian. Thus, for better approach on the small angle, the equation is:
其中g是地球的重力加速度。式4中的负号表示F力对θ角运动的方向。因为F等于sin(θ)而不是θ本身，因此运动不是简单的调和运动(GHS)。但是，如果θ很小，那么当角度以弧度表示时，sin(θ)几乎等于θ。因此，为了在小角度上更好地逼近，式为:
$$F=-mg\sin (\theta )\approx mg\theta \dots \dots \dots \dots (5)$$

By substituting s = lθ, or θ = s/l to equation (5), then the equation will be:

将式(5)代入s = lθ或θ= s/l，则式(5)为:
$$F\approx -\frac{mg}{l}s\dots \dots \dots \dots (6)$$
​

Here, for small movement, motion can be modeled as simple harmonic motion. Because, equation (6) as appropriate with Hooke law, F = –kx, where x is equal with the length of arch s and spring constant equal with k = mg/l. If the spring constant $k=mg/l$is substituted to equation $T=2\pi \sqrt{\frac{m}{k}}$

在这里，对于小的运动，可以将运动建模为简谐运动。因为，根据胡克定律，式(6)F = -kx，其中x等于弧的长度s，弹簧常数等于$k=mg/l$。如果弹簧常数k = mg/l代入式$T=2\pi \sqrt{\frac{m}{k}}$
$$T=2\pi \sqrt{\frac{\frac{m}{mg}}{l}}\dots \dots \dots \dots （7）$$

$$T=2\pi \sqrt{\frac{l}{g}}\dots \dots \dots \dots （8）$$

Meanwhile, the frequency of simple pendulum can be written as the following: 同时，单摆的频率可表示为:
$$f=2\pi \sqrt{\frac{g}{l}}\dots \dots \dots \dots （9）$$

From equations (8) and (9) it is known that the period of simple pendulum does not depend on mass and deviation angle of pendulum, but it depends on the length and acceleration of gravitation. The value of acceleration gravitation can be counted based on equation (8) which is:

由式(8)和式(9)可知，单摆周期不取决于质量和摆偏角，而是取决于重力的长度和加速度。加速度重力由式(8)计算，即:
$$g=\frac{4{\pi }^{2}l}{r^2}\dots \dots \dots \dots （10）$$

EXPERIMENTAL SETUP

Hardware Design

Hardware in this experiment are Hall effect sensor, push button, arduino, LCD, LED and power supply. Hall effect sensor and push button as the input for the hardware. Arduino is the controller device with function to process data on input signal and output signal sent to actuator. LCD display and LED function as output to display the result of data acquisition. The diagram of hardware is shown in Fig. 2, whereas electrical circuit is shown in Fig. 3. Hardware diagram shows Hall effect sensor that function as detector to control object motion when passing through the point of balance. Every object that passes the point of balance the output signal of Hall effect sensor will change. This change of signal that becomes input for arduino to count the quantity of oscillation and control time counting. Digital output pin from Hall effect sensor will be interfaced by arduino on digital pin 2.

实验硬件包括霍尔传感器、按钮、arduino、LCD、LED和电源。硬件采用霍尔效应传感器和按钮作为输入。Arduino是对输入信号和输出信号发送给执行器的数据进行处理的控制器设备。LCD显示和LED作为输出，显示数据采集结果。硬件框图如图2所示，电路如图3所示。硬件图显示霍尔效应传感器作为探测器，控制物体通过平衡点时的运动。每一个经过平衡点的物体，霍尔效应传感器的输出信号都会发生变化。这个信号的变化成为arduino计数振荡量和控制时间计数的输入。霍尔效应传感器的数字输出引脚将被arduino连接到数字引脚2上。

Push button functions as input button for controlling the quantity of oscillation, starting measurement and reset the hardware. Push button to control the quantity of oscillation consist of three buttons namely “+” for adding oscillation quantity, “-“ for decreasing oscillation quantity and “ok” for stating the input of oscillation quantity to arduino. Interfacing each button respectively with the arduino on digital pin 5, 6 and 7. Whereas button for measurement is interfaced with arduino on digital pin 3 and 4. Arduino functions as device for controlling and processing data. Arduino controls all input signal and send output signal to actuator based on data processing result. Data processing processed by arduino is managing input signal from sensor and push button to count quantity and oscillation time as well as displaying the counting result on LCD. Time measurement is done using timer1 component of arduino controlled by timer overflow interruption with the quantity of resolution 10 ms. LCD functions as the displayer and interfaced by arduino on SDA and SCL pin because the LCD uses 12C communication. While LED functions as indicator lamp and interface with the arduino digital pin 4, 5, and 6.

按钮作为输入按钮，控制振荡量，开始测量和硬件复位。振荡量控制按钮由“+”增加振荡量、“-”减少振荡量、“ok”向arduino说明振荡量输入三个按钮组成。将每个按钮分别与数字引脚5、6和7上的arduino连接。而测量按钮与arduino的数字引脚3和4接口。Arduino作为控制和处理数据的设备。Arduino控制所有输入信号，并根据数据处理结果将输出信号发送给执行器。arduino处理的数据处理是管理来自传感器和按钮的输入信号，计数数量和振荡时间，并将计数结果显示在LCD上。时间测量使用arduino的timer1组件，由定时器溢出中断控制，分辨率为10 ms。LCD作为显示器，由于使用12C通信，由SDA和SCL引脚上的arduino进行接口。LED作为指示灯，与arduino数字引脚4,5,6接口。

FIGURE 2. Hardware experiment setup.

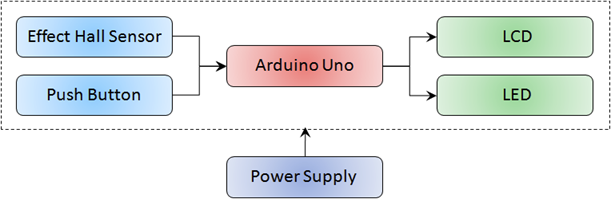
FIGURE 3. Hardware electrical circuit.

Software Tools

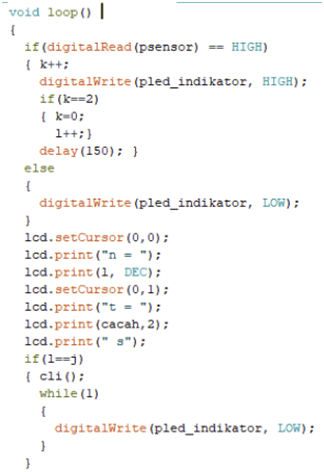
Software in experiment uses arduino programing based on C code. Software is embedded to arduino by using Integrated Development Environment (IDE) arduino compiler. The developed software consists of some blocks, they are header declaration, arduino pins declaration, definitions of variable, timer function maker, interrupt timer maker, setup input/output, reading push button input to manage the quantity of oscillation, reading Hall effect sensor input, create if function, and writing the counting result on LCD display. The main block of software is shown in Fig. 4.

实验软件采用基于C语言的arduino编程。通过集成开发环境(IDE)的arduino编译器将软件嵌入到arduino中。所开发的软件包括报头声明、arduino引脚声明、变量定义、定时器函数生成器、中断计时器生成器、设置输入/输出、读取按钮输入以管理振荡量、读取霍尔效应传感器输入、创建if函数、将计数结果写入LCD显示屏等模块。软件的主块如图4所示。

FIGURE 4. Main block of development software

Mechanical Setup

Experiment mechanic device setup consist of stative scaffolder completed with protractor to measure deviation angle, object hanged up using rope, magnetic sensor and electronic box completed with various of hardware. Besides that, the experiment is also completed with some measurement devices namely digital scales to measure object mass and ruler to measure the length of rope. Accuracy of measurement of the digital scales used is 0.01 g, meanwhile accuracy of ruler used is 1 mm. Set-up of mechanic device for simple pendulum is shown in Fig. 5.

实验机械装置设置包括用量角器完成的静态支架、用绳子吊起的物体、磁传感器和用各种硬件完成的电子箱。此外，实验还使用了测量设备，即测量物体质量的数字天平和测量绳子长度的尺子。所用数字天平的测量精度为0.01 g，所用尺的测量精度为1 mm。单摆机械装置的设置如图5所示。

FIGURE 5. Mechanical setup of simple pendulum experiment.

EXPERIMENTAL RESULT AND DISCUSSION

The experiment was conducted to investigate the effect of the length of rope, object mass, and angle deviation toward oscillation period and frequency as well as determining acceleration of gravitation. The parameters measured in this experiment are oscillation quantity, oscillation time, rope length, object mass and deviation angle. Data collection is done to investigate the effect of rope length and determining the acceleration of gravitation is presented in Table 1. Data collection is conducted by establishing quantity of constant oscillation as many as 3 times, object mass is 37.95 g and deviation angle is 3°. The period of oscillation is obtained using equation (2) and frequency of oscillation is obtained using equation 2. While acceleration of gravitation is obtained using equation (10). The analysis result revealed the value of acceleration of gravitation is 9.87 ± 0.06 m/s² with percentage of error is 0.71% if compared to theoretic value which is 9.8 m/s². The experiment is supported by a similar study conducted by Oliveira in which the result of acceleration of gravitation reached 9.8 ± 0.01 m/s² [6]. Pili and Violanda conducted similar study to measure acceleration of gravitation on simple pendulum system using ultrasonic sensor and arduino in which g value was 9.82 ± 0.1 m/s² and the percentage of error was 0.4% [15].

实验研究了绳子长度、物体质量和角度偏差对振动周期和频率的影响以及重力加速度的确定。本实验测量的参数为振荡量、振荡时间、绳子长度、物体质量和偏离角。收集数据来研究绳子长度的影响，并确定重力加速度如表1所示。建立3次恒振荡量，物体质量37.95 g，偏移角3°进行数据采集。振荡周期由式(2)得到，振荡频率由式(2)得到。而重力加速度则由式(10)求得。分析结果表明，重力加速度为9.87±0.06 m/s2，与理论值9.8 m/s²的误差百分比为0.71%。该实验得到了Oliveira所做的类似研究的支持，其重力加速度的结果达到9.8±0.01 m/s²[6]。Pili和Violanda也做过类似的研究，利用超声波传感器和arduino在单摆系统上测量重力加速度，g值为9.82±0.1 m/s²，误差百分比为0.4%[15]。

TABLE 1. Data tabulation on the effect of rope length toward oscilation period and frequency.

l (m)	t (s)	T (s)	f (Hz)	g (m/s2)
0.20	2.68	0.89	1.12	9.88 ± 0.08
0.25	3.00	1.00	1.00	9.86 ± 0.07
0.30	3.28	1.09	0.91	9.90 ± 0.06
0.35	3.54	1.18	0.85	9.91 ± 0.06
0.40	3.80	1.27	0.79	9.83 ± 0.05
0.45	4.03	1.34	0.74	9.83 ± 0.05
0.50	4.24	1.41	0.71	9.87 ± 0.05
			Average	9.87 ± 0.06

The effect of rope length on oscillation period was analyzed using regression method and the result is shown in graph as on Fig. 6. The result of regression analysis is 𝑦= 2.002𝑥^0.501 with correlation coefficient of data is 0.999. The graphic shows relation between oscillation period and rope length in which y period and x is rope length. The equation of gained shows that oscillation period is equal with the rope length. The result is appropriate with theoretic analysis as in equation (8) that $T\approx \sqrt{l}$ . Coefficient value of 2.002 shows series$\frac{2\pi }{\sqrt{g}}$ ，therefore the value of acceleration of gravitation can be determined through $g=(\frac{2\pi }{2.002}{)}^2=9.84m/s^2$. The percentage of error is 0.45% if compared to theoretic value of acceleration of gravitation which is 9.8 m/s². This experiment result also supported by the study done by Pili and Violanda that the square of oscillation period is equal with the rope length [16].

采用回归法分析了绳长对振荡周期的影响，结果如图6所示。回归分析结果为𝑦= 2.002𝑥^0.501，数据相关系数为0.999。图示振荡周期与绳子长度的关系，其中y周期与x为绳子长度。得到的方程表明，摆动周期与绳长相等。如式(8)所示:$T\approx \sqrt{l}$，其结果与理论分析相符。系数值为2.002为级数$\frac{2\pi }{\sqrt{g}}$，因此重力加速度的值可以通过$g=(\frac{2\pi }{2.002}{)}^2=9.84m/s^2$来确定。与重力加速度理论值$9.8m/s^2$相比，误差为0.45%。这一实验结果也得到了Pili和Violanda所做的振荡周期的平方等于绳长[16]的研究的支持。

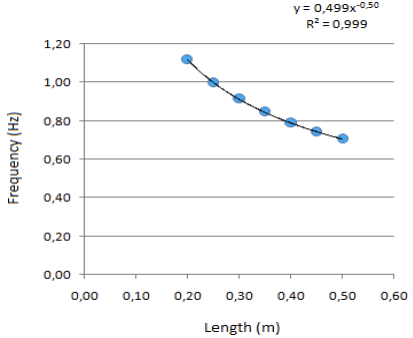
Relying on the measurement result shown in Table 1 can be seen that the rope length also influences oscillation frequency. Analysis of the rope length effect toward oscillation frequency was done using regression method as revealed in Fig. 7. The result of regression is shown through equation 𝑦= 0.499𝑥^-0.50 with correlation coefficient of data is 0.999. The graphic shows relationship between oscillation frequency and rope length in which y is frequency of oscillation and x is rope length. The equation gained shows that oscillation frequency is equal with one per rope length root. The result is appropriate with theoretic analysis as in equation (9) that $T\approx \frac{1}{l}$. Coefficient value of 0.499 shows series$\frac{\sqrt{g}}{2\pi }$,

由表1的测量结果可以看出，绳长也会影响振荡频率。采用回归法分析了绳长对振荡频率的影响，如图7所示。回归结果通过方程𝑦= 0.499𝑥^-0.50数据相关系数为0.999。图示振荡频率与绳长关系，其中y为振荡频率，x为绳长。得到的方程表明振荡频率等于每绳长根1次。与理论分析结果相吻合如式(9):$T\approx \frac{1}{l}$系数值为0.499表示级数$\frac{\sqrt{g}}{2\pi }$，

so the value of acceleration of gravitation can be determined with Font metrics not found for font: .. Error percentage of the result is 0.21% if compared to theoretic value of gravitation acceleration reaches 9.8 m/s². This experiment result is supported by the research of Yani and Asrizal in which the conclusion is the more length of rope results on longer oscillation period but smaller frequency [17].

所以重力加速度的值可以用 Font metrics not found for font: . 来确定。当重力加速度达到9.8 m/s²时，计算结果与理论值相比误差为0.21%。Yani和Asrizal的研究支持了这一实验结果，他们的结论是:绳子越长，振荡周期越长，频率[17]越小。

FIGURE 6. Graphic of the rope length effect toward period of oscillation.

FIGURE 7. Graphic of the rope length effect toward oscilation frequency.

The effect of object mass on oscillation period was investigated by doing variation on object mass. Meanwhile, rope length, angle deviation and oscillation quantity are constant. In this experiment, the length of rope used is 0.5 m, angle of deviation is 3°, and the quantity of oscillation is 3. The period of oscillation determined using Equation 1, while oscillation frequency is determined using equation (2). Measurement result is analyzed and presented in the form of data tabulation as shown in Table 2. Analysis result shows that object mass do not effect oscillation period and frequency in harmonic motion of simple pendulum. The condition is clearly shown in equations (8) and (9) that oscillation period and frequency are only influenced by length rope and gravitation acceleration.

通过对物体质量的变化，研究了物体质量对振动周期的影响。同时，绳子长度、角度偏差和振荡量不变。本实验中使用的绳子长度为0.5 m，偏离角度为3°，振荡次数为3次。振荡周期由式(1)确定，振荡频率由式(2)确定。对测量结果进行分析并以数据表的形式表示，如表2所示。分析结果表明，物体质量对单摆谐波运动的振荡周期和频率没有影响。由式(8)和式(9)可知，振荡周期和频率仅受绳长和重力加速度的影响。

The effect of angle deviation on oscillation period was investigated by doing variation toward angle deviation. Meanwhile length of rope, object mass and quantity of oscillation are constant. In this experiment, the length of rope used is 0.4 m, object mass is 37.95 g, and the amount of oscillation is 3. Oscillation period is determined using Equation 1, while oscillation frequency is determined using equation (2). Measurement result is analyzed and presented in the form of data tabulation as shown in Table 3. The result shows that deviation angle do not effect oscillation of period and frequency in harmonic motion of simple pendulum. The condition is clearly shown in equations (8) and (9) that oscillation period and frequency only effected by rope length and gravitation acceleration.

通过对角度偏差的变化，研究了角度偏差对振荡周期的影响。同时，绳子长度、物体质量和振荡量都是恒定的。本实验中使用的绳子长度为0.4 m，物体质量为37.95 g，振荡量为3。振荡周期由式(1)确定，振荡频率由式(2)确定。对测量结果进行分析并以数据表的形式表示，如表3所示。结果表明，在单摆谐波运动中，偏心角不影响周期和频率的振荡。由式(8)和式(9)可知，振荡周期和频率仅受绳长和重力加速度的影响

TABLE 2. Data tabulation of object mass effect toward oscillation period and frequency.

m (gr)	t (s)	T (s)	f (Hz)
37.95	4.24	1.41	0.71
50.18	4.26	1.42	0.70
74.87	4.26	1.42	0.70
101.32	4.24	1.41	0.71
125.46	4.25	1.42	0.71
151.02	4.26	1.42	0.71
200.45	4.27	1.42	0.70
249.65	4.24	1.41	0.71

TABLE 3. Data tabulation of deviation angle effect toward
oscillation period and frequency.

θ(°)	t(s)	T(s)	f(Hz)
1	4.02	1.34	0.75
2	4.02	1.34	0.75
3	4.07	1.36	0.74
4	4.12	1.37	0.73
5	4.12	1.37	0.73

CONCLUSION

Experiment of oscillation motion on simple pendulum by making use of Hall effect sensor and arduino has been conducted to find out oscillation period and frequency as well as measuring acceleration. The gravitation acceleration in this experiment is 9.87 ± 0.06 m/s2 with error percentage is 0.71% if compared to theoretic value is 9.8 m/s². The result shows that oscillation period is equal with rope length root, meanwhile oscillation frequency is equal with one per rope length root. Besides, the experiment result also shows that the object mass and deviation angle do not effects the oscillation period and frequency of simple pendulum system.

利用霍尔效应传感器和arduino对单摆进行了振动运动实验，得到了摆动周期和频率，并测量了加速度。本实验的重力加速度为9.87±0.06 m/s2，与理论值9.8 m/s²相比，误差为0.71%。结果表明，振荡周期与绳长根相等，振荡频率与每绳长根1次相等。此外，实验结果还表明，物体质量和偏移角不影响单摆系统的振荡周期和频率。

REFERENCES

REFERENCES

1. A. M. Chaudry, Phys. Teach. 58, 418–421 (2020).
2. E. C. Prima, S. Karim, S. Utari, R. Ramdani, E. R. R. Putri, and S. M. Darmawati, Procedia Eng. 170, 536–
   540 (2017).
3. I. Boimau and R. N. K. Mellu, Jurnal Ilmu Pendidik. Fis. 4, 45–46 (2019).
4. R. N. K. Mellu and I. Boimau, J. Pendidik. Fis. 8, 249–262, (2020).
5. V. T. O. Silva, R. N. De Medeiros, W. O. Silva, and S. R. R. Medeiros, Phys. Educ. 55, 045016 (2020).
6. V. Oliveira, Phys. Educ. 54, 053001 (2019)
7. E. Fontana, C. Yeung, and J. C. Hall, Phys. Teach. 58, 338–339 (2020).
8. L. A. Ladino and S. H. Rondón, Phys. Educ. 54, 025013 (2019).
9. A. A. Moya, Phys. Educ. 54, 015005 (2019).
10. U. Sari, Phys. Educ. 54, 035010 (2019).
11. U. Sari and T. Kirindi, J. Comput. Educ. Res. 7, 698–710 (2019).
12. A. Coban and N. Coban, Phys. Educ. 55, 043005 (2020).
13. R. Puantha, W. Khammarew, A. Tong-On, and P. Saphet, Phys. Educ. 54, 015009 (2019).
14. Z. Gingl, R. Mingesz, G. Makan, and J. Mellar, Phys. Educ. 54, 025010 (2019).
15. U. Pili and R. Violanda, Phys. Educ. 54, 015020 (2019).
16. U. Pili, R. Violanda, C. Ceniza, and R. Gomez, Phys. Educ. 53, 063001 (2018).
17. Yani, Pillar Phys. 12, 76–83 (2019).