4.2 张量积
4.2.1 定义
设 A = ( a i j ) m × n , B = ( b i j ) p × q , 则 称 如 下 分 块 矩 阵 ( a 11 B a 12 B ⋯ a 1 n B a 21 B a 22 B ⋯ a 2 n B ⋮ ⋮ ⋱ ⋮ a n 1 B a n 2 ⋯ a n n ) 为 A 与 B 的 张 量 积 记 作 A ⊗ B = ( a i j B ) m p × n q \begin{aligned} &设A=(a_{ij})_{m\times n},B=(b_{ij})_{p\times q},则称如下分块矩阵\left( \begin{matrix} a_{11}B&a_{12}B&\cdots&a_{1n}B\\ a_{21}B&a_{22}B&\cdots&a_{2n}B\\ \vdots&\vdots&\ddots&\vdots\\ a_{n1}B&a_{n2}&\cdots&a_{nn} \end{matrix} \right)为A与B的张量积\\ &记作A\otimes B=(a_{ij}B)_{mp\times nq} \end{aligned} 设A=(aij)m×n,B=(bij)p×q,则称如下分块矩阵⎝⎜⎜⎜⎛a11Ba21B⋮an1Ba12Ba22B⋮an2⋯⋯⋱⋯a1nBa2nB⋮ann⎠⎟⎟⎟⎞为A与B的张量积记作A⊗B=(aijB)mp×nq
eg
A
=
(
a
b
c
d
)
,
B
=
(
2
3
)
A=\left( \begin{matrix} a&b\\c&d \end{matrix} \right),B=\left( \begin{matrix} 2\\3 \end{matrix} \right)
A=(acbd),B=(23)
A ⊗ B = ( a B b B c B d B ) = ( 2 a 2 b 3 a 3 b 2 c 2 d 3 c 3 d ) , B ⊗ A = ( 2 A 3 B ) = ( 2 a 2 b 2 c 2 d 3 a 3 b 3 c 3 d ) \begin{aligned} &A\otimes B=\left( \begin{matrix} aB&bB\\cB&dB \end{matrix} \right)=\left( \begin{matrix} 2a&2b\\3a&3b\\2c&2d\\3c&3d \end{matrix} \right),B\otimes A=\left( \begin{matrix} 2A\\3B \end{matrix} \right)=\left( \begin{matrix} 2a&2b\\2c&2d\\3a&3b\\3c&3d \end{matrix} \right) \end{aligned} A⊗B=(aBcBbBdB)=⎝⎜⎜⎛2a3a2c3c2b3b2d3d⎠⎟⎟⎞,B⊗A=(2A3B)=⎝⎜⎜⎛2a2c3a3c2b2d3b3d⎠⎟⎟⎞
- 张量积不满足交换律
定理
- 两个上三角的张量积也是上三角
- 两个对角阵的张量积是对角阵
- I n ⊗ I m = I m ⊗ I n = I m × n I_n\otimes I_m=I_{m}\otimes I_n=I_{m\times n} In⊗Im=Im⊗In=Im×n
4.2.2 计算
a. 分块法
右进右出
(
A
B
C
D
)
⊗
F
=
(
A
⊗
F
B
⊗
F
C
⊗
F
D
⊗
F
)
(
A
B
)
⊗
F
=
(
A
⊗
F
B
⊗
F
)
\left( \begin{matrix} A&B\\C&D \end{matrix} \right)\otimes F=\left( \begin{matrix} A\otimes F&B\otimes F\\C\otimes F&D\otimes F \end{matrix} \right) (A\quad B)\otimes F=(A\otimes F\quad B\otimes F)
(ACBD)⊗F=(A⊗FC⊗FB⊗FD⊗F)(AB)⊗F=(A⊗FB⊗F)
一般情况下:
(
A
B
)
⊗
F
≠
(
A
⊗
F
B
⊗
F
)
(A\quad B) \otimes F\neq (A\otimes F\quad B\otimes F)
(AB)⊗F=(A⊗FB⊗F)

b. 向量与向量张量积
列 向 量 α = ( a 1 a 2 ⋮ a n ) β = ( b 1 b 2 ⋮ b q ) , 则 α ⊗ β = ( a 1 ⊗ β a 2 ⊗ β ⋮ a n ⊗ β ) n q × 1 = ( a 1 b 1 a 1 b 2 ⋮ a 1 b q ⋮ a n b 1 a n b 2 ⋮ a n b q ) n q × 1 列向量\alpha=\left( \begin{matrix} a_1\\a_2\\\vdots\\a_n \end{matrix} \right)\beta=\left( \begin{matrix} b_1\\b_2\\\vdots\\b_q \end{matrix} \right),则\alpha \otimes \beta=\left( \begin{matrix} a_1\otimes \beta\\a_2\otimes \beta\\\vdots\\a_n\otimes \beta \end{matrix} \right)_{nq\times 1}=\left( \begin{matrix} a_1b_1\\a_1b_2\\\vdots\\a_1b_q\\\vdots \\a_nb_1\\a_nb_2\\\vdots\\a_nb_q \end{matrix} \right)_{nq\times 1} 列向量α=⎝⎜⎜⎜⎛a1a2⋮an⎠⎟⎟⎟⎞β=⎝⎜⎜⎜⎛b1b2⋮bq⎠⎟⎟⎟⎞,则α⊗β=⎝⎜⎜⎜⎛a1⊗βa2⊗β⋮an⊗β⎠⎟⎟⎟⎞nq×1=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛a1b1a1b2⋮a1bq⋮anb1anb2⋮anbq⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞nq×1
c. 向量与矩阵张量积
列 向 量 α = ( a 1 a 2 ⋮ a m ) , B n × q = ( β 1 , β 2 , ⋯ , β q ) , α ⊗ B = ( a 1 B a 2 B ⋮ a m B ) = ( a 1 ( β 1 , β 2 , ⋯ , β q ) a 2 ( β 1 , β 2 , ⋯ , β q ) ⋮ a m ( β 1 , β 2 , ⋯ , β q ) ) = ( a 1 b 11 a 1 b 12 ⋯ a 1 b 1 q a 1 b 21 a 1 b 22 ⋯ a 1 b 2 q ⋮ ⋮ ⋱ ⋮ a 1 b p 1 a 1 b p 2 ⋯ a 1 b p q a 2 b 11 a 2 b 12 ⋯ a 2 b 1 q a 2 b 21 a 2 b 22 ⋯ a 2 b 2 q ⋮ ⋮ ⋱ ⋮ a 2 b p 1 a 2 b p 2 ⋯ a 2 b p q ⋮ ⋮ ⋮ ⋮ a m b 11 a m b 12 ⋯ a m b 1 q a m b 21 a m b 22 ⋯ a m b 2 q ⋮ ⋮ ⋱ ⋮ a m b p 1 a m b p 2 ⋯ a m b p q ) m p × q \begin{aligned} &列向量\alpha=\left( \begin{matrix} a_1\\a_2\\\vdots\\a_m \end{matrix} \right),B_{n\times q}=(\beta_1,\beta_2,\cdots,\beta_q),\\ &\alpha\otimes B=\left( \begin{matrix} a_1B\\a_2B\\\vdots\\a_mB \end{matrix} \right)=\left( \begin{matrix} a_1(\beta_1,\beta_2,\cdots,\beta_q)\\ a_2(\beta_1,\beta_2,\cdots,\beta_q)\\ \vdots\\ a_m(\beta_1,\beta_2,\cdots,\beta_q)\\ \end{matrix} \right)=\left( \begin{matrix} a_1b_{11}&a_1b_{12}&\cdots&a_1b_{1q}\\ a_1b_{21}&a_1b_{22}&\cdots&a_1b_{2q}\\ \vdots&\vdots&\ddots&\vdots\\ a_1b_{p1}&a_1b_{p2}&\cdots&a_1b_{pq}\\ a_2b_{11}&a_2b_{12}&\cdots&a_2b_{1q}\\ a_2b_{21}&a_2b_{22}&\cdots&a_2b_{2q}\\ \vdots&\vdots&\ddots&\vdots\\ a_2b_{p1}&a_2b_{p2}&\cdots&a_2b_{pq}\\ \vdots&\vdots&\vdots&\vdots\\ a_mb_{11}&a_mb_{12}&\cdots&a_mb_{1q}\\ a_mb_{21}&a_mb_{22}&\cdots&a_mb_{2q}\\ \vdots&\vdots&\ddots&\vdots\\ a_mb_{p1}&a_mb_{p2}&\cdots&a_mb_{pq}\\ \end{matrix} \right)_{mp\times q} \end{aligned} 列向量α=⎝⎜⎜⎜⎛a1a2⋮am⎠⎟⎟⎟⎞,Bn×q=(β1,β2,⋯,βq),α⊗B=⎝⎜⎜⎜⎛a1Ba2B⋮amB⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛a1(β1,β2,⋯,βq)a2(β1,β2,⋯,βq)⋮am(β1,β2,⋯,βq)⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛a1b11a1b21⋮a1bp1a2b11a2b21⋮a2bp1⋮amb11amb21⋮ambp1a1b12a1b22⋮a1bp2a2b12a2b22⋮a2bp2⋮amb12amb22⋮ambp2⋯⋯⋱⋯⋯⋯⋱⋯⋮⋯⋯⋱⋯a1b1qa1b2q⋮a1bpqa2b1qa2b2q⋮a2bpq⋮amb1qamb2q⋮ambpq⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞mp×q
4.2.3 性质
-
k ( A ⊗ B ) = ( k A ) ⊗ B = A ⊗ ( k B ) k(A\otimes B)=(kA)\otimes B=A\otimes (kB) k(A⊗B)=(kA)⊗B=A⊗(kB)
-
分配律: ( A + B ) ⊗ C = A ⊗ C + B ⊗ C (A+B)\otimes C=A\otimes C+B\otimes C (A+B)⊗C=A⊗C+B⊗C , C ⊗ ( A + B ) = C ⊗ A + C ⊗ B C\otimes(A+B)=C\otimes A+C\otimes B C⊗(A+B)=C⊗A+C⊗B
-
结合律: ( A ⊗ B ) ⊗ C = A ⊗ ( B ⊗ C ) (A\otimes B)\otimes C=A\otimes (B\otimes C) (A⊗B)⊗C=A⊗(B⊗C)
-
吸收律: ( A ⊗ B ) ( C ⊗ D ) = ( A C ) ⊗ ( B D ) (A\otimes B)(C\otimes D)=(AC)\otimes (BD) (A⊗B)(C⊗D)=(AC)⊗(BD)
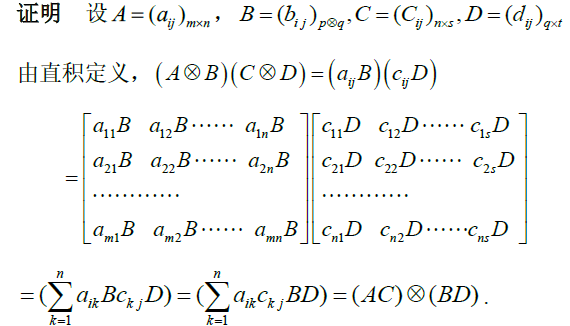
推论:
若 A = A m × m 为 m 阶 方 阵 , B = B n × n 为 n 阶 方 阵 , 则 ( A ⊗ B ) k = A k ⊗ B k ( A ⊗ I n ) ( I m ⊗ B ) = A ⊗ B \begin{aligned} &若A=A_{m\times m}为m阶方阵,B=B_{n\times n}为n阶方阵,则\\ &(A\otimes B)^k=A^k\otimes B^k\\ &(A\otimes I_n)(I_m\otimes B)=A\otimes B \end{aligned} 若A=Am×m为m阶方阵,B=Bn×n为n阶方阵,则(A⊗B)k=Ak⊗Bk(A⊗In)(Im⊗B)=A⊗B( A 1 ⊗ B 1 ) ( A 2 ⊗ B 2 ) ⋯ ( A k ⊗ B k ) = ( A 1 A 2 ⋯ A k ) ⊗ ( B 1 ⊗ B 2 ⋯ B k ) ( A 1 ⊗ A 2 ⊗ ⋯ ⊗ A k ) ( B 1 ⊗ B 2 ⊗ ⋯ ⊗ B k ) = ( A 1 B 1 ) ⊗ ( A 2 ⊗ ⋯ ⊗ A k ) ( B 2 ⊗ ⋯ ⊗ B k ) = ( A 1 B 1 ) ⊗ ( A 2 B 2 ) ⊗ ⋯ ⊗ ( A k B k ) \begin{aligned} &(A_1\otimes B_1)(A_2\otimes B_2)\cdots(A_k\otimes B_k)=(A_1A_2\cdots A_k)\otimes (B_1\otimes B_2\cdots B_k)\\ &(A_1\otimes A_2\otimes \cdots\otimes A_k)(B_1\otimes B_2\otimes \cdots\otimes B_k)=(A_1B_1)\otimes(A_2\otimes \cdots\otimes A_k)(B_2\otimes \cdots\otimes B_k)=(A_1B_1)\otimes (A_2B_2)\otimes \cdots \otimes (A_kB_k) \end{aligned} (A1⊗B1)(A2⊗B2)⋯(Ak⊗Bk)=(A1A2⋯Ak)⊗(B1⊗B2⋯Bk)(A1⊗A2⊗⋯⊗Ak)(B1⊗B2⊗⋯⊗Bk)=(A1B1)⊗(A2⊗⋯⊗Ak)(B2⊗⋯⊗Bk)=(A1B1)⊗(A2B2)⊗⋯⊗(AkBk)
eg:
A = A m × m , 证 明 e A ⊗ I n = e A ⊗ I n A=A_{m\times m},证明e^{A\otimes I_n}=e^A\otimes I_n A=Am×m,证明eA⊗In=eA⊗Ine A ⊗ I n = ∑ k = 1 ∞ 1 k ! ( A ⊗ I ) k = ∑ k = 1 ∞ 1 k ! ( A k ⊗ I k ) = ( ∑ k = 1 ∞ 1 k ! A k ) ⊗ I k = e A ⊗ I \begin{aligned} &e^{A\otimes I_n}=\sum_{k=1}\limits^\infty\frac{1}{k!}(A\otimes I)^k=\sum_{k=1}\limits^\infty\frac{1}{k!}(A^k\otimes I^k)=(\sum_{k=1}\limits^\infty\frac{1}{k!}A^k)\otimes I^k=e^A\otimes I \end{aligned} eA⊗In=k=1∑∞k!1(A⊗I)k=k=1∑∞k!1(Ak⊗Ik)=(k=1∑∞k!1Ak)⊗Ik=eA⊗I
-
转置公式:
( A ⊗ B ) H = A H ⊗ B H ( A ⊗ B ) − 1 = A − 1 ⊗ B − 1 \begin{aligned} &(A\otimes B)^H=A^H\otimes B^H\\ &(A\otimes B)^{-1}= A^{-1}\otimes B^{-1} \end{aligned} (A⊗B)H=AH⊗BH(A⊗B)−1=A−1⊗B−1 -
若A与B都是U阵,则 A ⊗ B A\otimes B A⊗B U阵
-
秩公式: r ( A ⊗ B ) = r ( A ) r ( B ) r(A\otimes B)=r(A)r(B) r(A⊗B)=r(A)r(B)
推论:
若 X 1 、 ⋯ 、 X p 为 C m 中 p 个 线 性 无 关 的 列 向 量 , Y 1 、 ⋯ 、 Y q 为 C n 中 q 个 线 性 无 关 列 向 量 , 则 则 p q 个 列 向 量 ( X i ⊗ Y j ) 线 性 无 关 \begin{aligned} &若X_1、\cdots、X_p为C^m中p个线性无关的列向量,Y_1、\cdots、Y_q为C^n中q个线性无关列向量,则\\ &则pq个列向量(X_i\otimes Y_j)线性无关 \end{aligned} 若X1、⋯、Xp为Cm中p个线性无关的列向量,Y1、⋯、Yq为Cn中q个线性无关列向量,则则pq个列向量(Xi⊗Yj)线性无关
由于 r ( { X ⊗ Y } ) = r ( { X } ) r ( { Y } ) r(\{X\otimes Y\})=r(\{X\})r(\{Y\}) r({X⊗Y})=r({X})r({Y}) ,张量积的秩等于两个向量组的秩的乘积,所以张量积线性无关
4.2.4 张量积行列式
设
A
=
(
a
i
j
)
∈
C
m
×
m
,
B
=
(
b
i
j
)
∈
C
n
×
n
A=(a_{ij}) \in C^{m\times m} ,B=(b_{ij})\in C^{n\times n}
A=(aij)∈Cm×m,B=(bij)∈Cn×n ,则
t
r
(
A
⊗
B
)
=
t
r
(
A
)
∗
t
r
(
B
)
∣
A
⊗
B
∣
=
∣
A
∣
n
∣
B
∣
m
\begin{aligned} &tr(A\otimes B)=tr(A)*tr(B)\\ &\vert A\otimes B \vert=\vert A \vert^n\vert B \vert^m \end{aligned}
tr(A⊗B)=tr(A)∗tr(B)∣A⊗B∣=∣A∣n∣B∣m
证明:
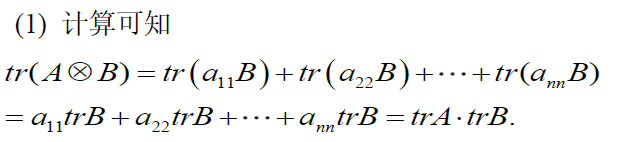
由 许 尔 公 式 , 存 在 可 逆 阵 P 使 P − 1 A P = ( λ 1 ∗ ⋱ 0 λ m ) 为 上 三 角 , 且 P ⊗ I 为 可 逆 阵 , 构 造 一 个 新 公 式 ( P ⊗ I ) − 1 A ⊗ B ( P ⊗ I ) = ( P − 1 A P ) ⊗ B = A 1 ⊗ B = ( λ 1 B ( ∗ B ) λ 2 B ⋱ 0 λ m B ) 故 ∣ A ⊗ B ∣ = ∣ λ 1 n B ∣ ∣ λ 2 n B ∣ ⋯ ∣ λ m n B ∣ m = ∣ λ 1 n λ 2 n ⋯ λ m n ∣ ∣ B ∣ m = ∣ A ∣ n ∣ B ∣ m \begin{aligned} &由许尔公式,存在可逆阵P使P^{-1}AP=\left( \begin{matrix} \lambda_1&&*\\ &\ddots&\\ 0&&\lambda_m \end{matrix} \right)为上三角,且P\otimes I为可逆阵,构造一个新公式\\ &(P\otimes I)^{-1}A\otimes B(P\otimes I)=(P^{-1}AP)\otimes B=A_1\otimes B=\left( \begin{matrix} \lambda_1B&&&(*B)\\ &\lambda_2B&&\\ &&\ddots&\\ 0&&&\lambda_mB \end{matrix} \right)\\ &故\vert A\otimes B \vert=\vert \lambda_1^nB\vert\vert \lambda_2^nB\vert\cdots\vert \lambda_m^nB\vert^m=\vert \lambda_1^n\lambda_2^n\cdots\lambda_m^n\vert\vert B \vert^m = \vert A \vert^n\vert B\vert ^m \end{aligned} 由许尔公式,存在可逆阵P使P−1AP=⎝⎛λ10⋱∗λm⎠⎞为上三角,且P⊗I为可逆阵,构造一个新公式(P⊗I)−1A⊗B(P⊗I)=(P−1AP)⊗B=A1⊗B=⎝⎜⎜⎛λ1B0λ2B⋱(∗B)λmB⎠⎟⎟⎞故∣A⊗B∣=∣λ1nB∣∣λ2nB∣⋯∣λmnB∣m=∣λ1nλ2n⋯λmn∣∣B∣m=∣A∣n∣B∣m
4.2.5 张量积特征值特征向量
特征值
若 A = A m × m 的 特 征 根 为 λ 1 , λ 2 , ⋯ , λ m , B = B n × n 的 特 征 根 为 t 1 , t 2 , ⋯ , t n , 则 A ⊗ B 的 全 体 特 征 根 为 m n 个 数 { λ k t j } , ( k = 1 , 2 , ⋯ , m j = 1 , 2 , ⋯ , n ) \begin{aligned} &若A=A_{m\times m} 的特征根为\lambda_1,\lambda_2,\cdots,\lambda_m,B=B_{n\times n} 的特征根为t_1,t_2,\cdots,t_n,则\\ &A\otimes B的全体特征根为mn个数\{\lambda_kt_j\},(k=1,2,\cdots,m\quad j=1,2,\cdots,n) \end{aligned} 若A=Am×m的特征根为λ1,λ2,⋯,λm,B=Bn×n的特征根为t1,t2,⋯,tn,则A⊗B的全体特征根为mn个数{λktj},(k=1,2,⋯,mj=1,2,⋯,n)
特征向量
设 { X 1 , ⋯ , X p } 是 A ∈ C m × m 关 于 λ 的 线 性 无 关 的 特 征 向 量 , { Y 1 , ⋯ , Y q } 是 B ∈ C n × n 关 于 t 的 线 性 无 关 的 特 征 向 量 , 则 p q 个 向 量 { X i ⊗ Y j } 是 A ⊗ B 关 于 λ t 的 特 征 向 量 \begin{aligned} &设\{X_1,\cdots,X_p\}是A\in C^{m\times m}关于\lambda的线性无关的特征向量,\{Y_1,\cdots,Y_q\}是B\in C^{n\times n}关于t的线性\\ &无关的特征向量,则pq个向量 \{X_i\otimes Y_j\} 是A\otimes B关于\lambda t的特征向量 \end{aligned} 设{X1,⋯,Xp}是A∈Cm×m关于λ的线性无关的特征向量,{Y1,⋯,Yq}是B∈Cn×n关于t的线性无关的特征向量,则pq个向量{Xi⊗Yj}是A⊗B关于λt的特征向量

eg

A = ( 2 2 1 3 ) ⊗ ( 1 − 1 0 1 ) = B ⊗ D , 且 B 为 行 和 等 矩 阵 , B 为 对 角 阵 , 则 λ ( A ) = { 4 , t r ( A ) − 4 } = { 4 , 1 } , λ ( B ) = { 1 , 1 } ∴ A ⊗ B = ∏ λ A λ B = { 4 , 4 , 1 , 1 } , 特 式 ∣ λ I − A ∣ = ( λ − 4 ) 2 ( λ − 1 ) 2 可 知 , ( 1 1 ) ( − 2 1 ) 是 B 的 一 个 特 征 向 量 , ( 1 0 ) 是 D 的 特 征 值 , 故 A ⊗ B 的 特 征 向 量 为 ( 1 0 1 0 ) , ( − 2 0 1 0 ) \begin{aligned} &A=\left( \begin{matrix} 2&2\\1&3 \end{matrix} \right)\otimes \left( \begin{matrix} 1&-1\\0&1 \end{matrix} \right)=B\otimes D,且B为行和等矩阵,B为对角阵,则\lambda(A)=\{4,tr(A)-4\}=\{4,1\},\lambda(B)=\{1,1\}\\ &\therefore A\otimes B=\prod\lambda_A\lambda_B=\{4,4,1,1\},特式\vert \lambda I-A\vert=(\lambda-4)^2(\lambda-1)^2\\ &可知,\left( \begin{matrix} 1\\1 \end{matrix} \right)\left( \begin{matrix} -2\\1 \end{matrix} \right)是B的一个特征向量,\left( \begin{matrix} 1\\0 \end{matrix} \right)是D的特征值,故A\otimes B的特征向量为\left( \begin{matrix} 1\\0\\1\\0 \end{matrix} \right),\left( \begin{matrix} -2\\0\\1\\0 \end{matrix} \right) \end{aligned} A=(2123)⊗(10−11)=B⊗D,且B为行和等矩阵,B为对角阵,则λ(A)={4,tr(A)−4}={4,1},λ(B)={1,1}∴A⊗B=∏λAλB={4,4,1,1},特式∣λI−A∣=(λ−4)2(λ−1)2可知,(11)(−21)是B的一个特征向量,(10)是D的特征值,故A⊗B的特征向量为⎝⎜⎜⎛1010⎠⎟⎟⎞,⎝⎜⎜⎛−2010⎠⎟⎟⎞
A ⊗ I ± I ⊗ B A\otimes I\pm I\otimes B A⊗I±I⊗B