基础解系

基础解系的概念是针对方程而言的；齐次线性方程组的解集的最大无关组称为齐次线性方程的基础解系；要求齐次线性方程组的通解，只需求出它的基础解系。
【例】

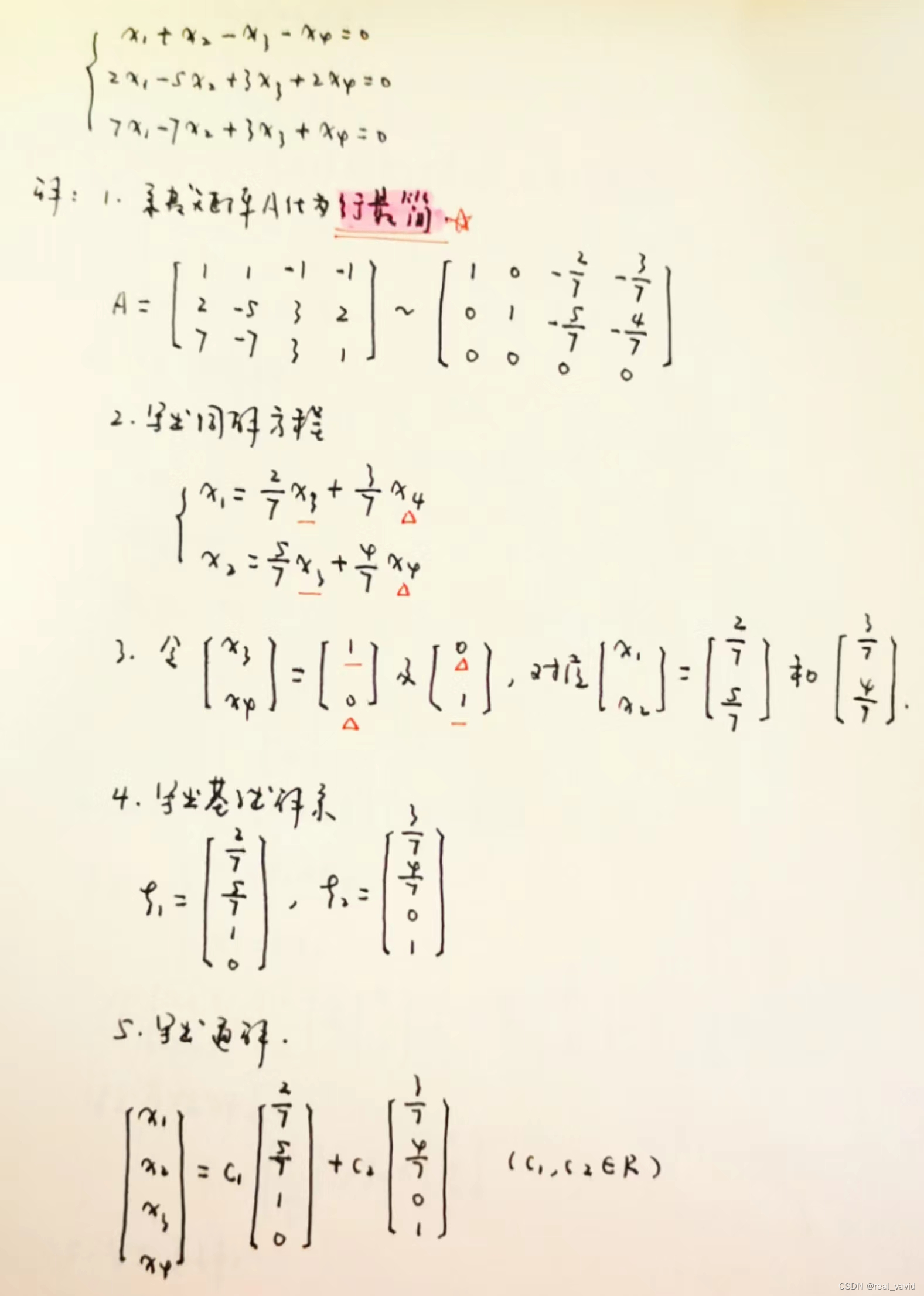
特征向量

特征向量和特征值满足关系式 $A\alpha =\lambda \alpha$；特征向量是相对于矩阵（方阵）而言的，一个方程组可以提取它的系数产生出一个矩阵，于是求解特征向量与求解系数矩阵非常类似。

【2019年数二】已知A，B相似，求可逆矩阵P，使得 $P^{-1}AP=B$
$A=\left[\begin{array}{ccc}-2& -2& 1\\ 2& 3& -2\\ 0& 0& -2\end{array}\right]$

$B=\left[\begin{array}{ccc}2& 1& 0\\ 0& -1& 0\\ 0& 0& -2\end{array}\right]$

【分析】A，B相似，特征值相同，求得 ${\lambda }_1=-2$，${\lambda }_2=-1$，${\lambda }_3=2$ $(特征值的求解过程省略，非本文章讲解的重点)$

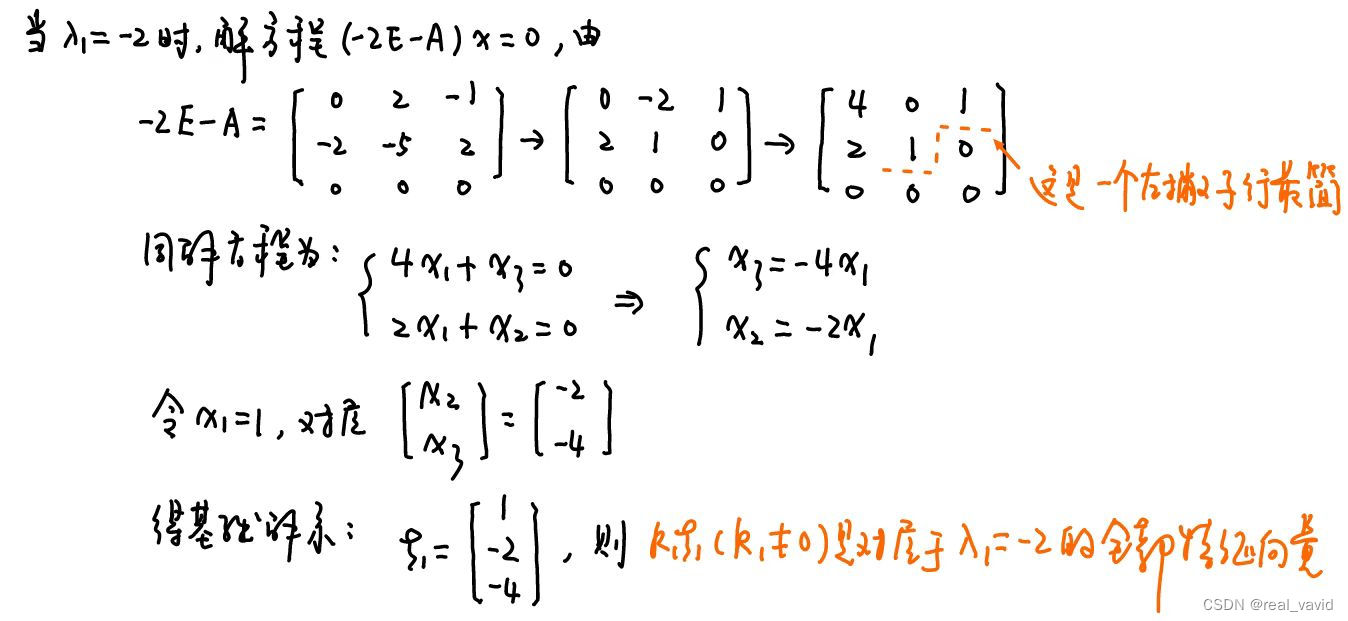
注：这里其实只要求出基础解系就好，为了讲解特征向量的求法，顺带写出了特征向量，即 $k_1{\xi }_1$；
另外，在化行最简的时候，书上面一般是从往左上角爬楼梯的行最简，有时候也可以化为往右上角爬楼梯的行最简（姑且称为「左撇子行最简」），同样也方便得到基础解系；

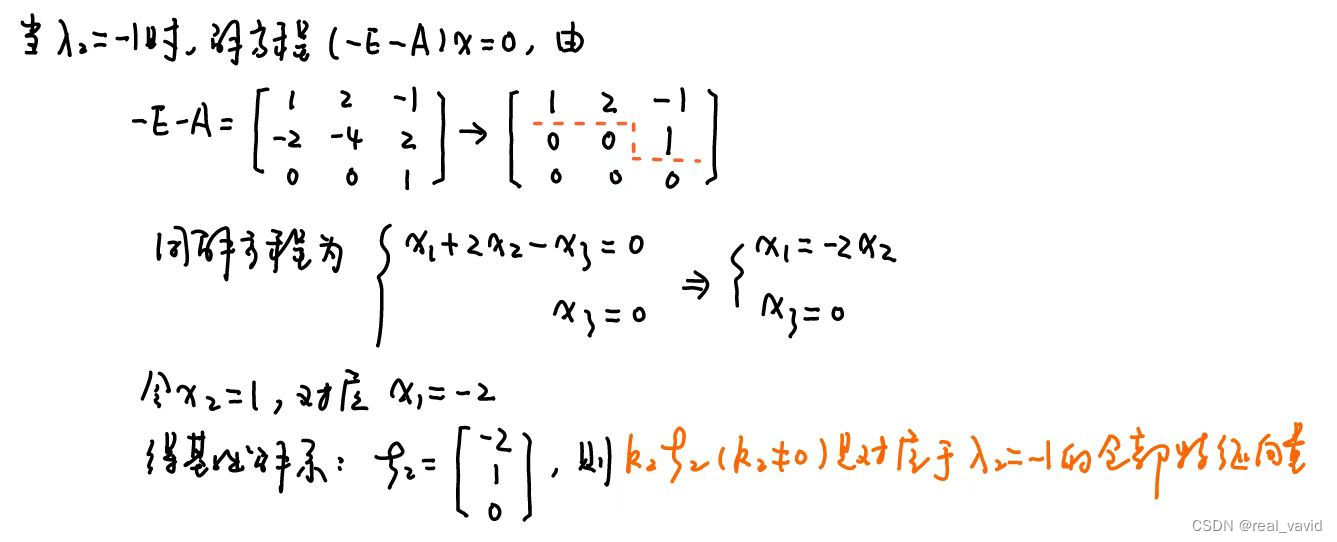
注：在化行最简时，可以直接将一行写为0，因为我们是通过$\left|\lambda E-A\right|$求得的$\lambda$，再将$\lambda$带入之后得到的矩阵必然是不可逆矩阵，里面的行线性相关，即就是对应的方程组中存在多余方程，因此选数字复杂的行直接写为0，可以简化计算过程，下同

熟悉以上过程后，先将矩阵化为行最简，然后直接将行最简不是1的那一列对应的未知数令为1，得到其余的未知数的值，进而写出对应的基础解系；这也是多数题目的参考答案给出的简化后的写法，很多学生一开始看不懂。

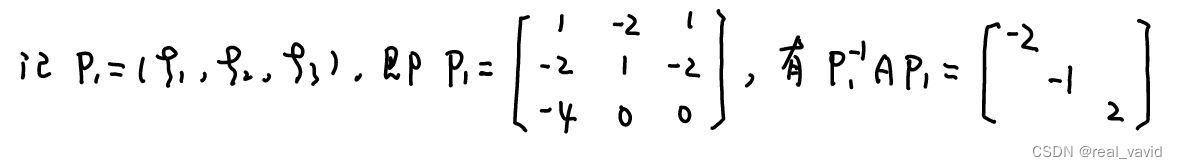
同理，分别计算矩阵B的特征值${\lambda }_1=-2$，${\lambda }_2=-1$，${\lambda }_3=2$ 对应的特征方程的基础解系：

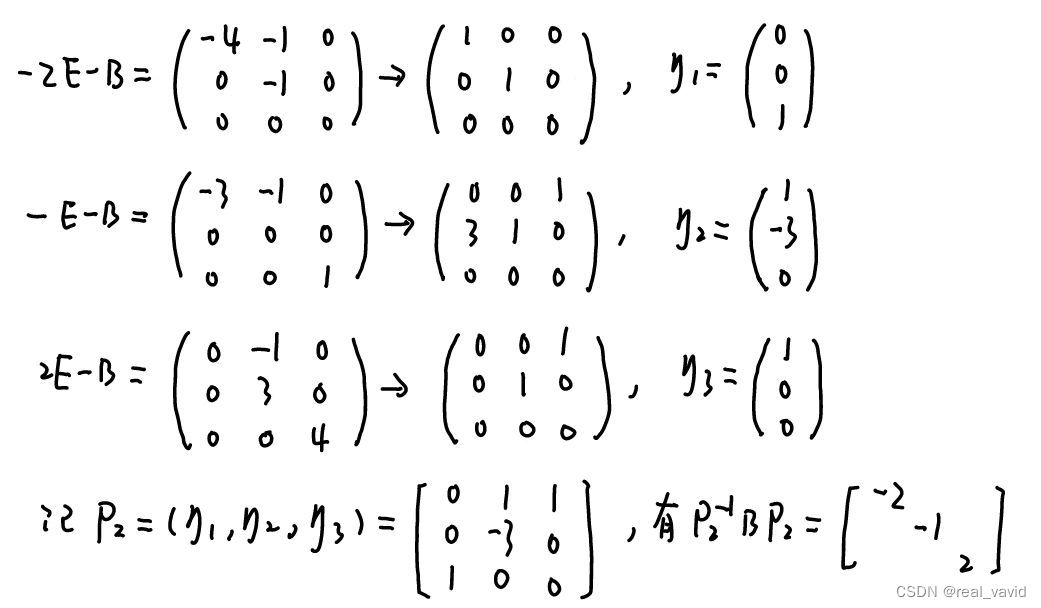
由于A、B相似，于是有：


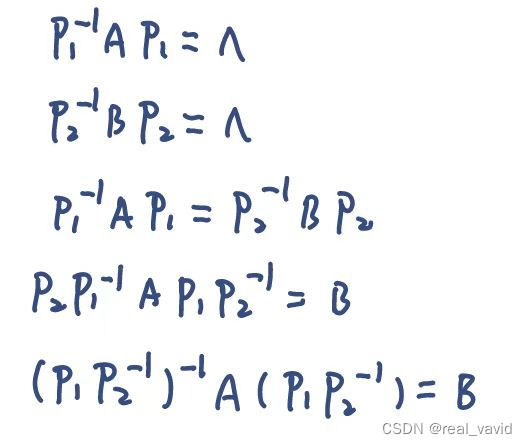
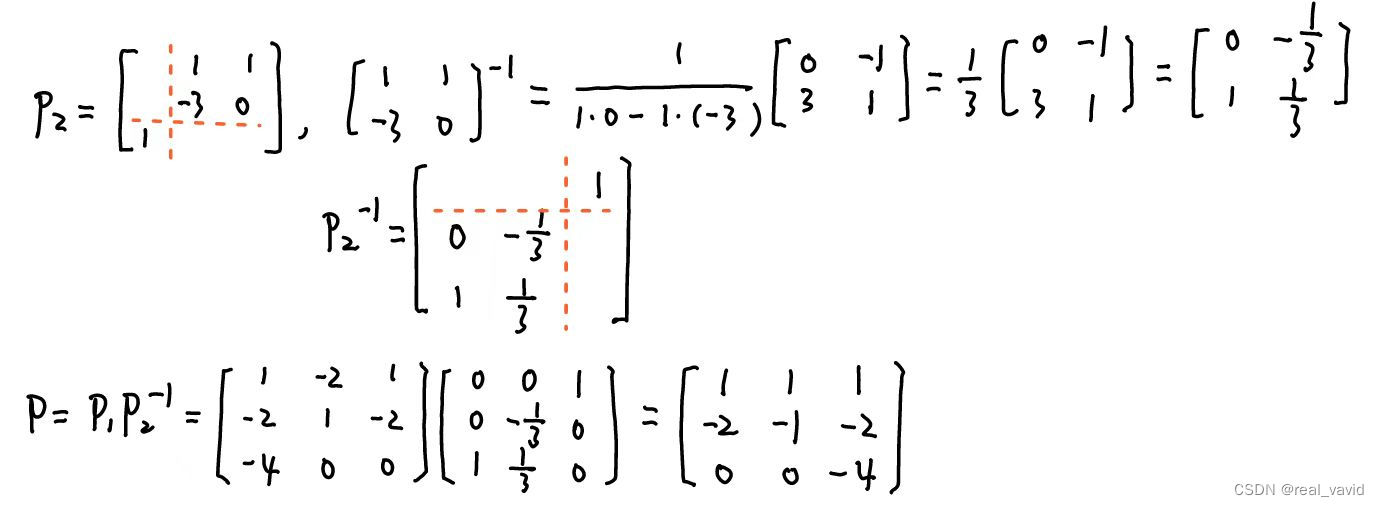
这里P可逆，为题目所求的可逆矩阵，且$P^{-1}AP=B$

传送门

求可逆矩阵可参考链接: 线代——求逆矩阵的快捷方法