堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
堆排序介绍
学习堆排序之前,有必要了解堆!若读者不熟悉堆,建议先了解堆(建议可以通过二叉堆,左倾堆,斜堆,二项堆或斐波那契堆等文章进行了解),然后再来学习本章。
我们知道,堆分为"最大堆"和"最小堆"。最大堆通常被用来进行"升序"排序,而最小堆通常被用来进行"降序"排序。 鉴于最大堆和最小堆是对称关系,理解其中一种即可。本文将对最大堆实现的升序排序进行详细说明。
最大堆进行升序排序的基本思想: ① 初始化堆: 将数列a[1...n]构造成最大堆。 ② 交换数据: 将a[1]和a[n]交换,使a[n]是a[1...n]中的最大值;然后将a[1...n-1]重新调整为最大堆。 接着,将a[1]和a[n-1]交换,使a[n-1]是a[1...n-1]中的最大值;然后将a[1...n-2]重新调整为最大值。 依次类推,直到整个数列都是有序的。
下面,通过图文来解析堆排序的实现过程。注意实现中用到了"数组实现的二叉堆的性质"。 在第一个元素的索引为 0 的情形中:
性质一: 索引为i的左孩子的索引是 (2*i+1);
性质二: 索引为i的右孩子的索引是 (2*i+2);
性质三: 索引为i的父结点的索引是 floor((i-1)/2);
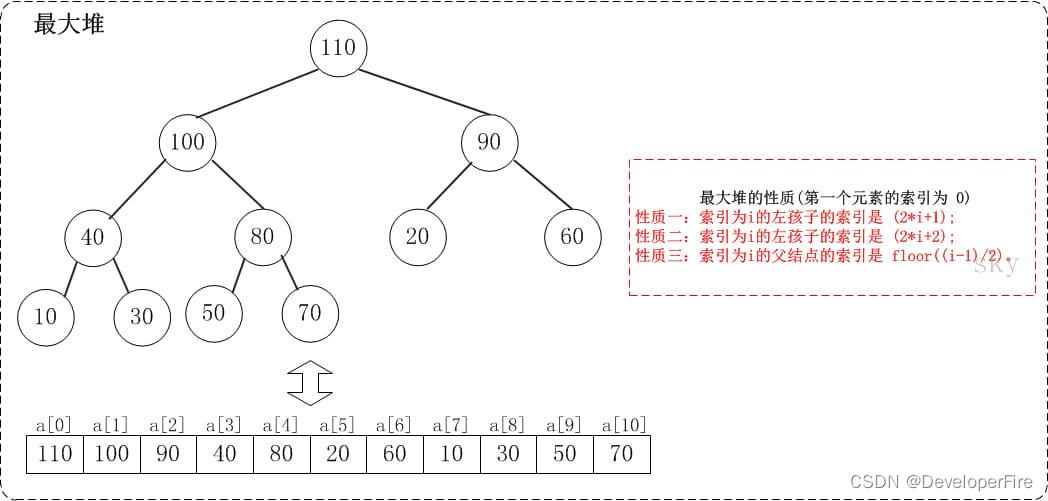
例如,对于最大堆{110,100,90,40,80,20,60,10,30,50,70}而言: 索引为0的左孩子的所有是1;索引为0的右孩子是2;索引为8的父节点是3。
堆排序实现
下面演示heap_sort_asc(a, n)对a={20,30,90,40,70,110,60,10,100,50,80}, n=11进行堆排序过程。下面是数组a对应的初始化结构:
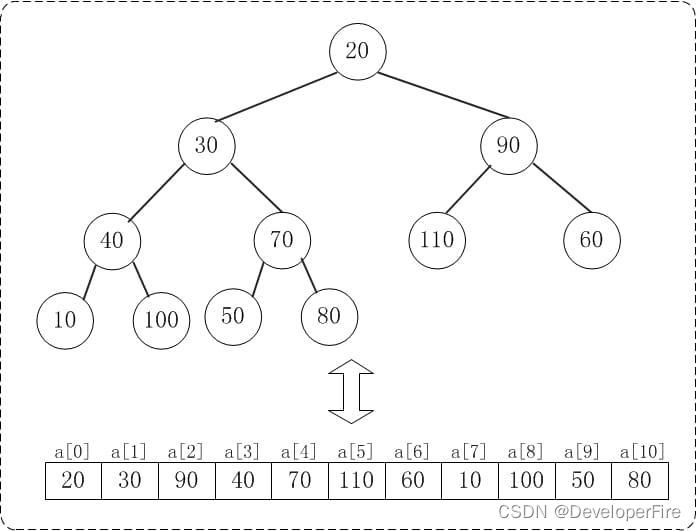
初始化堆
在堆排序算法中,首先要将待排序的数组转化成二叉堆。 下面演示将数组{20,30,90,40,70,110,60,10,100,50,80}转换为最大堆{110,100,90,40,80,20,60,10,30,50,70}的步骤。
1.1 i=11/2-1,即i=4

上面是maxheap_down(a, 4, 9)调整过程。maxheap_down(a, 4, 9)的作用是将a[4...9]进行下调;a[4]的左孩子是a[9],右孩子是a[10]。调整时,选择左右孩子中较大的一个(即a[10])和a[4]交换。
1.2 i=3
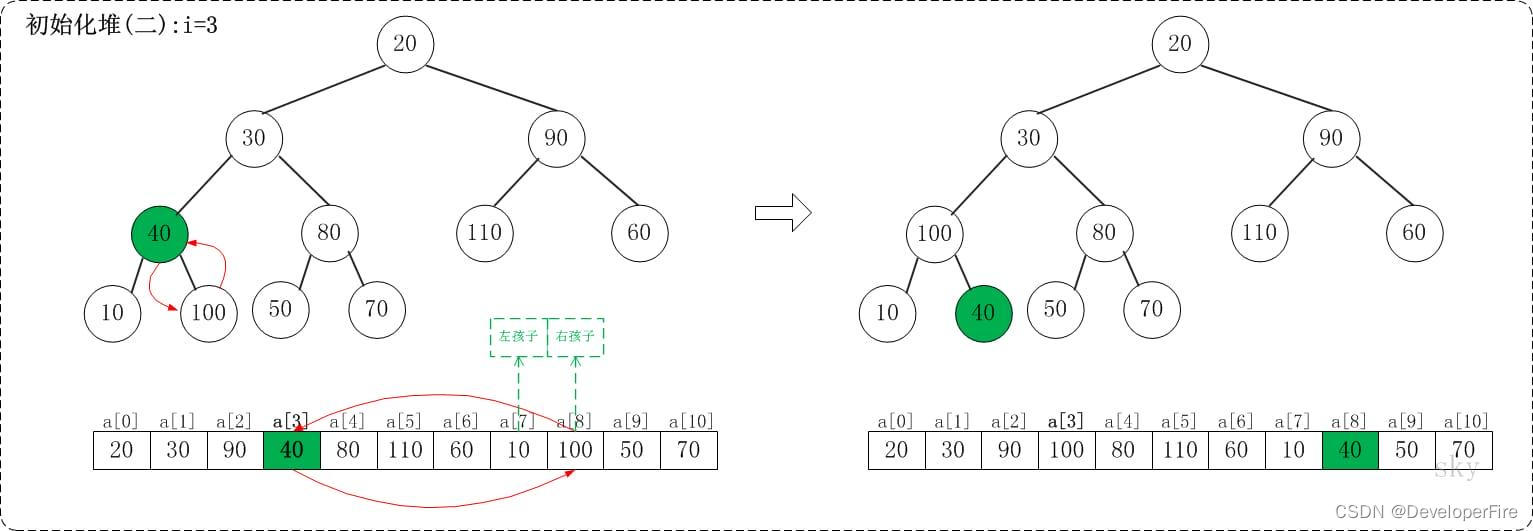
上面是maxheap_down(a, 3, 9)调整过程。maxheap_down(a, 3, 9)的作用是将a[3...9]进行下调;a[3]的左孩子是a[7],右孩子是a[8]。调整时,选择左右孩子中较大的一个(即a[8])和a[4]交换。
1.3 i=2
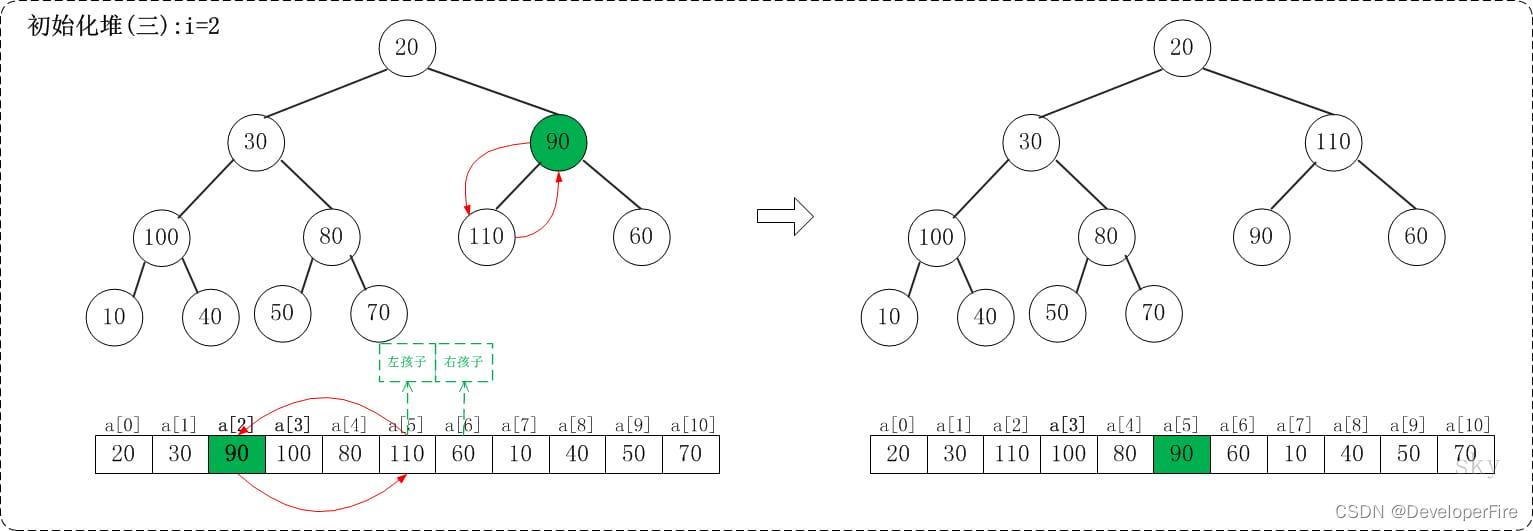
上面是maxheap_down(a, 2, 9)调整过程。maxheap_down(a, 2, 9)的作用是将a[2...9]进行下调;a[2]的左孩子是a[5],右孩子是a[6]。调整时,选择左右孩子中较大的一个(即a[5])和a[2]交换。
1.4 i=1

上面是maxheap_down(a, 1, 9)调整过程。maxheap_down(a, 1, 9)的作用是将a[1...9]进行下调;a[1]的左孩子是a[3],右孩子是a[4]。调整时,选择左右孩子中较大的一个(即a[3])和a[1]交换。交换之后,a[3]为30,它比它的右孩子a[8]要大,接着,再将它们交换。
1.5 i=0
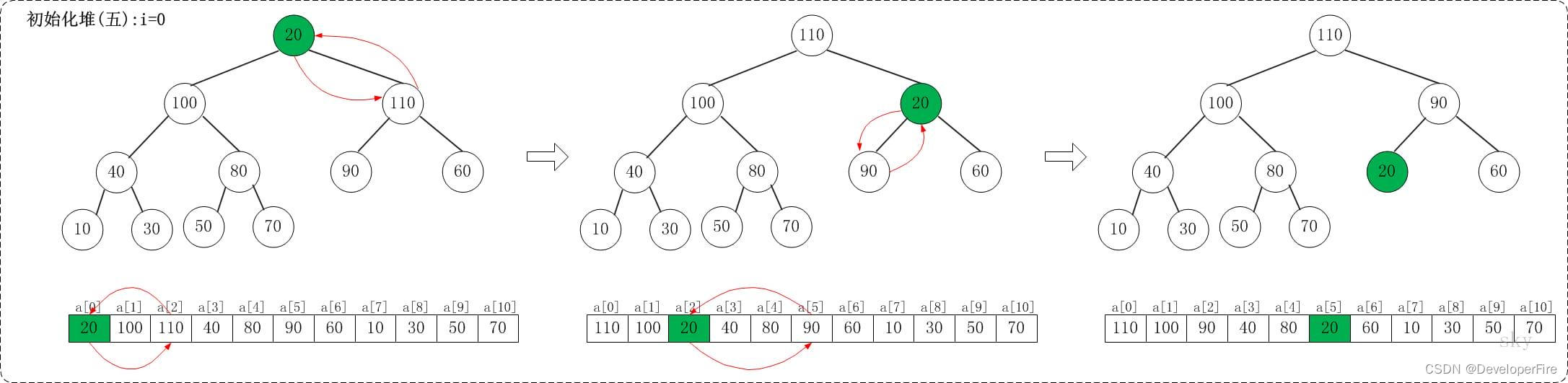
上面是maxheap_down(a, 0, 9)调整过程。maxheap_down(a, 0, 9)的作用是将a[0...9]进行下调;a[0]的左孩子是a[1],右孩子是a[2]。调整时,选择左右孩子中较大的一个(即a[2])和a[0]交换。交换之后,a[2]为20,它比它的左右孩子要大,选择较大的孩子(即左孩子)和a[2]交换。
调整完毕,就得到了最大堆。此时,数组{20,30,90,40,70,110,60,10,100,50,80}也就变成了{110,100,90,40,80,20,60,10,30,50,70}。
交换数据
在将数组转换成最大堆之后,接着要进行交换数据,从而使数组成为一个真正的有序数组。 交换数据部分相对比较简单,下面仅仅给出将最大值放在数组末尾的示意图。
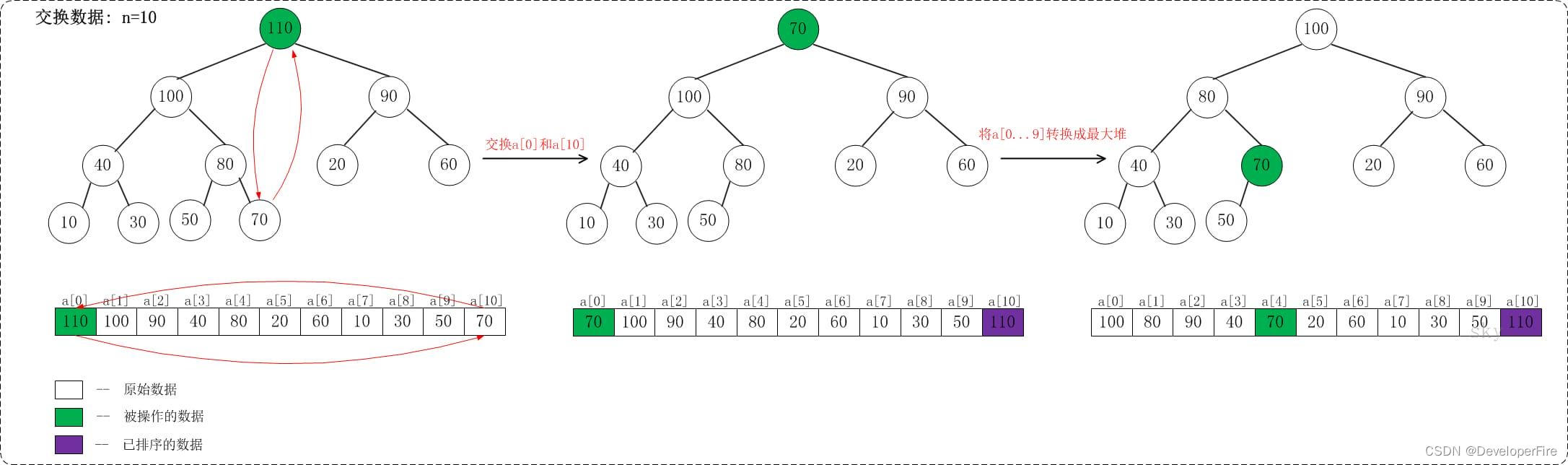
上面是当n=10时,交换数据的示意图。 当n=10时,首先交换a[0]和a[10],使得a[10]是a[0...10]之间的最大值;然后,调整a[0...9]使它称为最大堆。交换之后: a[10]是有序的! 当n=9时, 首先交换a[0]和a[9],使得a[9]是a[0...9]之间的最大值;然后,调整a[0...8]使它称为最大堆。交换之后: a[9...10]是有序的! ... 依此类推,直到a[0...10]是有序的。
堆排序复杂度和稳定性
堆排序时间复杂度
堆排序的时间复杂度是O(N*lgN)。
假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N),需要遍历多少次呢? 堆排序是采用的二叉堆进行排序的,二叉堆就是一棵二叉树,它需要遍历的次数就是二叉树的深度,而根据完全二叉树的定义,它的深度至少是lg(N+1)。最多是多少呢? 由于二叉堆是完全二叉树,因此,它的深度最多也不会超过lg(2N)。因此,遍历一趟的时间复杂度是O(N),而遍历次数介于lg(N+1)和lg(2N)之间;因此得出它的时间复杂度是O(N*lgN)。
堆排序稳定性
堆排序是不稳定的算法,它不满足稳定算法的定义。它在交换数据的时候,是比较父结点和子节点之间的数据,所以,即便是存在两个数值相等的兄弟节点,它们的相对顺序在排序也可能发生变化。
算法稳定性 -- 假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的!
代码实现
/**
* 堆排序: Java
*
* @author skywang
* @date 2014/03/11
*/
public class HeapSort {
/*
* (最大)堆的向下调整算法
*
* 注: 数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
* 其中,N为数组下标索引值,如数组中第1个数对应的N为0。
*
* 参数说明:
* a -- 待排序的数组
* start -- 被下调节点的起始位置(一般为0,表示从第1个开始)
* end -- 截至范围(一般为数组中最后一个元素的索引)
*/
public static void maxHeapDown(int[] a, int start, int end) {
int c = start; // 当前(current)节点的位置
int l = 2*c + 1; // 左(left)孩子的位置
int tmp = a[c]; // 当前(current)节点的大小
for (; l <= end; c=l,l=2*l+1) {
// "l"是左孩子,"l+1"是右孩子
if ( l < end && a[l] < a[l+1])
l++; // 左右两孩子中选择较大者,即m_heap[l+1]
if (tmp >= a[l])
break; // 调整结束
else { // 交换值
a[c] = a[l];
a[l]= tmp;
}
}
}
/*
* 堆排序(从小到大)
*
* 参数说明:
* a -- 待排序的数组
* n -- 数组的长度
*/
public static void heapSortAsc(int[] a, int n) {
int i,tmp;
// 从(n/2-1) --> 0逐次遍历。遍历之后,得到的数组实际上是一个(最大)二叉堆。
for (i = n / 2 - 1; i >= 0; i--)
maxHeapDown(a, i, n-1);
// 从最后一个元素开始对序列进行调整,不断的缩小调整的范围直到第一个元素
for (i = n - 1; i > 0; i--) {
// 交换a[0]和a[i]。交换后,a[i]是a[0...i]中最大的。
tmp = a[0];
a[0] = a[i];
a[i] = tmp;
// 调整a[0...i-1],使得a[0...i-1]仍然是一个最大堆。
// 即,保证a[i-1]是a[0...i-1]中的最大值。
maxHeapDown(a, 0, i-1);
}
}
/*
* (最小)堆的向下调整算法
*
* 注: 数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
* 其中,N为数组下标索引值,如数组中第1个数对应的N为0。
*
* 参数说明:
* a -- 待排序的数组
* start -- 被下调节点的起始位置(一般为0,表示从第1个开始)
* end -- 截至范围(一般为数组中最后一个元素的索引)
*/
public static void minHeapDown(int[] a, int start, int end) {
int c = start; // 当前(current)节点的位置
int l = 2*c + 1; // 左(left)孩子的位置
int tmp = a[c]; // 当前(current)节点的大小
for (; l <= end; c=l,l=2*l+1) {
// "l"是左孩子,"l+1"是右孩子
if ( l < end && a[l] > a[l+1])
l++; // 左右两孩子中选择较小者
if (tmp <= a[l])
break; // 调整结束
else { // 交换值
a[c] = a[l];
a[l]= tmp;
}
}
}
/*
* 堆排序(从大到小)
*
* 参数说明:
* a -- 待排序的数组
* n -- 数组的长度
*/
public static void heapSortDesc(int[] a, int n) {
int i,tmp;
// 从(n/2-1) --> 0逐次遍历每。遍历之后,得到的数组实际上是一个最小堆。
for (i = n / 2 - 1; i >= 0; i--)
minHeapDown(a, i, n-1);
// 从最后一个元素开始对序列进行调整,不断的缩小调整的范围直到第一个元素
for (i = n - 1; i > 0; i--) {
// 交换a[0]和a[i]。交换后,a[i]是a[0...i]中最小的。
tmp = a[0];
a[0] = a[i];
a[i] = tmp;
// 调整a[0...i-1],使得a[0...i-1]仍然是一个最小堆。
// 即,保证a[i-1]是a[0...i-1]中的最小值。
minHeapDown(a, 0, i-1);
}
}
public static void main(String[] args) {
int i;
int a[] = {20,30,90,40,70,110,60,10,100,50,80};
System.out.printf("before sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
heapSortAsc(a, a.length); // 升序排列
//heapSortDesc(a, a.length); // 降序排列
System.out.printf("after sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
}
}


![如何在 Mac 上将 PDF 转换为 Word [6 种免费方法]](https://img-blog.csdnimg.cn/img_convert/67b1e5a8e9b582ae46afe7c5d08aecb1.png)