1.1 离散时间信号——序列

1.1.1 序列

离散时间信号只在离散时间上给出函数值，是时间上不连续的序列。一 般 ，离散时间的间隔是均匀的，以$T$表示，故用 $x(nT)$表示此离散时间信号在$nT$点上的值，$n$为整数。
$x(n)$可以看成是对模拟信号$x_a(t)$的等间隔抽样
$x(n)=x_a(t){|}_{t=nT}=x_a(nT)$

注意

1. $n$必须是整数。不是整数时，在相邻两个抽样之间的时刻并未抽样，而信号并不一定等于零 。只要满足抽样定理要求（以下将要讨论），则抽样点之间的信号可以通过低通平滑滤波器的插值作用来恢复。
2. 模拟信号也可以采用非等间隔时间抽样（但不是这门课说的）
3. 序列的表示方法

(1)函数表示法$x(n)=a^{n}u(n)$
(2)数列的表示方法 x ( n ) = { … , − 5 , − 3 , 2 , 7 , … } x(n)=\{…,-5,-3,2,7,…\} x(n)={…,−5,−3,2,7,…}
(3)图形表示法

1.1.2 序列的运算

数字信号处理中，序列的运算都是通过三个基本运算单元—— 加法器、乘法器和延时单元实现的。
序列运算可以有三类，一类是基于对序列幅度$x(n)$的运算；一类是基于对序列变量$n$的运算；一类是基于既对幅度$x(n)$，又对变量$n$的运算。

1、基于幅度的运算

（1）加法 $z(n)=x(n)+y(n)$
（2）乘法$w(n)=x(n)y(n)$
（3）累加$y(n)={\sum }_{n=-\infty }^{\infty }x(k)$
（4）序列的绝对和$S={\sum }_{n=-\infty }^{\infty }|x(n)|$
当 $S=B<\infty$称序列$x(n)$为绝对可和序列，序列的绝对可和性对于判断序列的傅里叶变换是否存在以及判断系统是否稳定有极重要意义
（5）序列的能量定义：$E[x(n)]={\sum }_{n=-\infty }^{\infty }|x(n){|}^2$，当$E[x(n)]={\sum }_{n=-\infty }^{\infty }|x(n){|}^2=A<\infty$则称$x(n)$为能量信号
（6）序列的平均功率定义：$P[x(n)]=li{m}_{N\to \infty }\frac{1}{2N+1}{\sum }_{n=-N}^N|x(n){|}^2$，若极限存在，则是功率信号
一般来说.周期信号、随机信号的存在时间是无限的，因此它们不是能量信号而是功率信号。对于周期信号，只需取一个周期^的平均功率即可。
$P[x(n)]=\frac{1}{N}{\sum }_{n=0}^{N-1}|x(n){|}^2$

2、基于对变量的运算

（1）移位
（2）翻褶
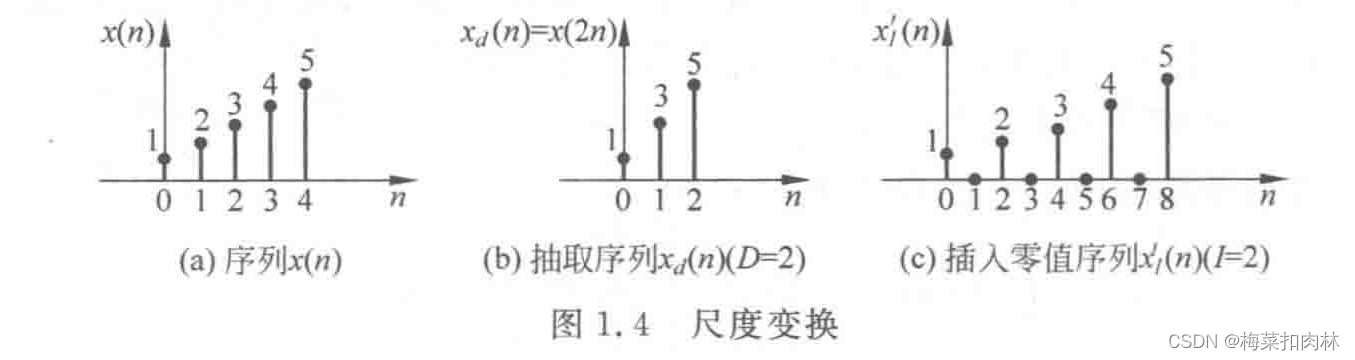
（3）时间尺度变换

• 抽取（下抽样变换）抽取是为了减小抽样频率
• 插值（上抽样变换）插值是为了增加抽样频率
  

3、既对幅度运算又对变量运算

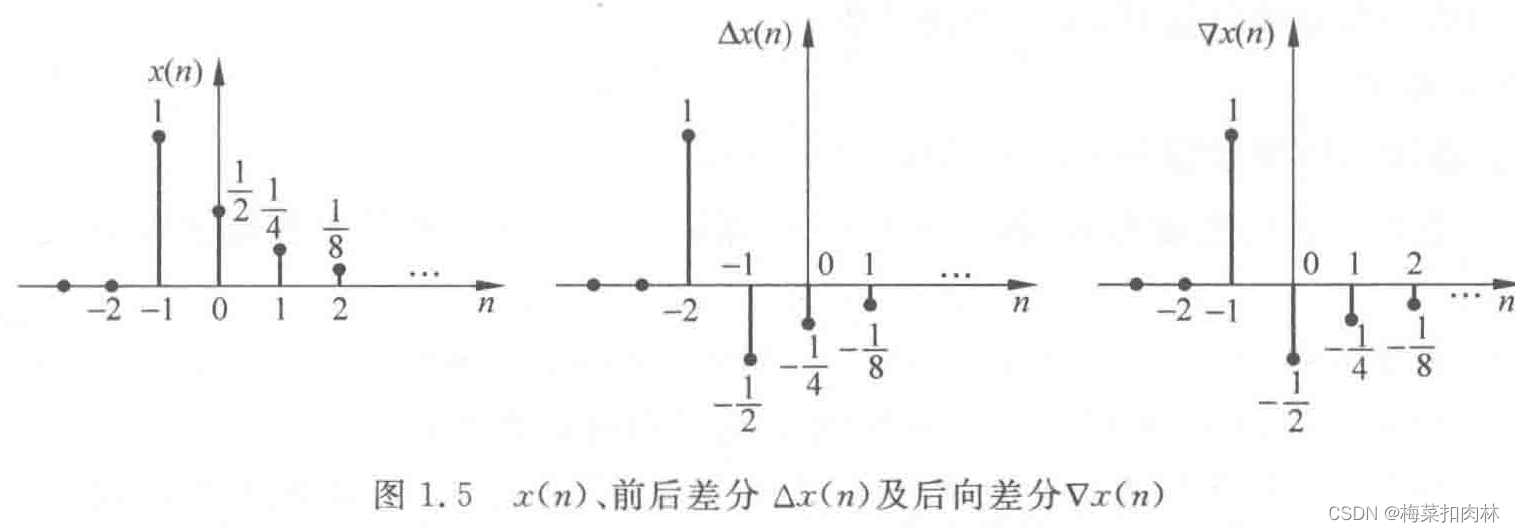
（1）差分运算
前向差分$△x(n)=x(n+1)-x(n)$
后向差分$▽x(n)=x(x)-x(n-1)$
由此得出$▽x(n)=△x(n-1)$

（2）卷积和运算
$$y(n)=x(n)\ast h(n)=\sum _{m=-\infty }^{\infty }x(m)h(n-m)=\sum _{m=-\infty }^{\infty }x(n-m)h(m)$$
（3）相关运算
$$r_{xy}(m)=\sum _{n=-\infty }^{\infty }x(n)y(n-m)$$
（4）奇分量和偶分量

• 对于复序列
  $$x_e(n)=\frac{1}{2}[x(n)+x^{\ast }(-n)]$$
  $$x_o(n)=\frac{1}{2}[x(n)-x^{\ast }(-n)]$$
• 对于实序列
  $$x_e(n)=\frac{1}{2}[x(n)+x^{(}-n)]$$
  $$x_o(n)=\frac{1}{2}[x(n)-x^{(}-n)]$$