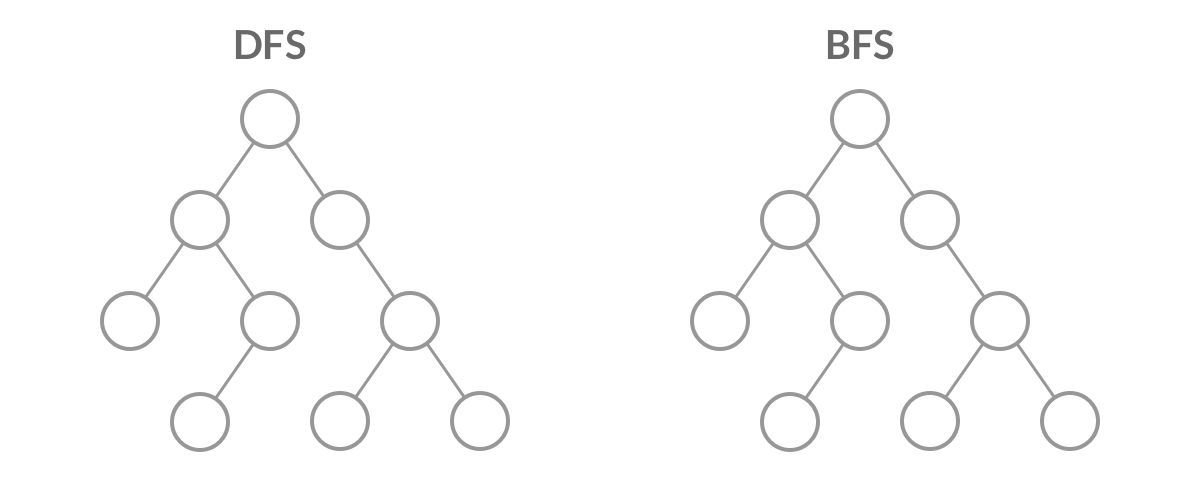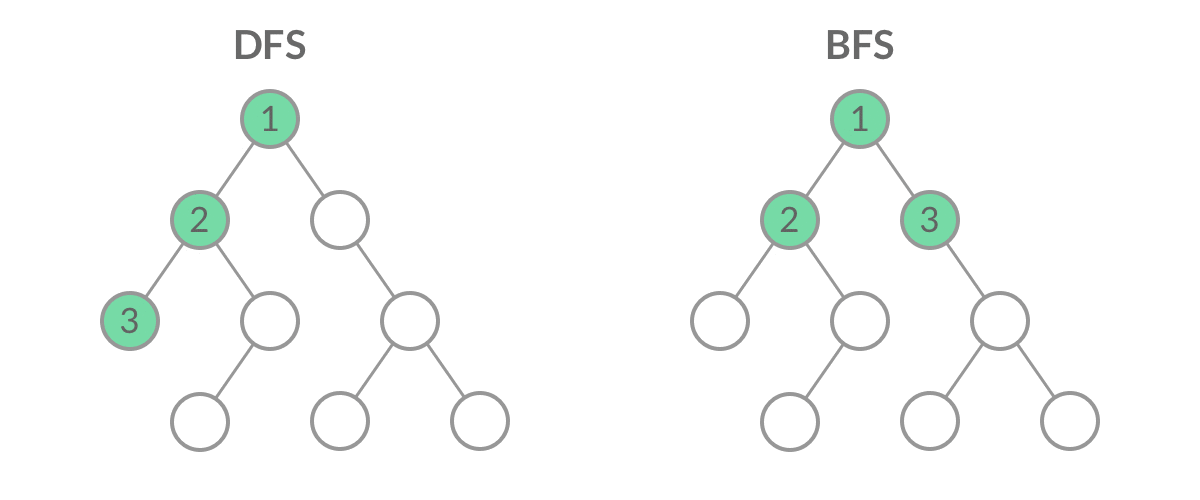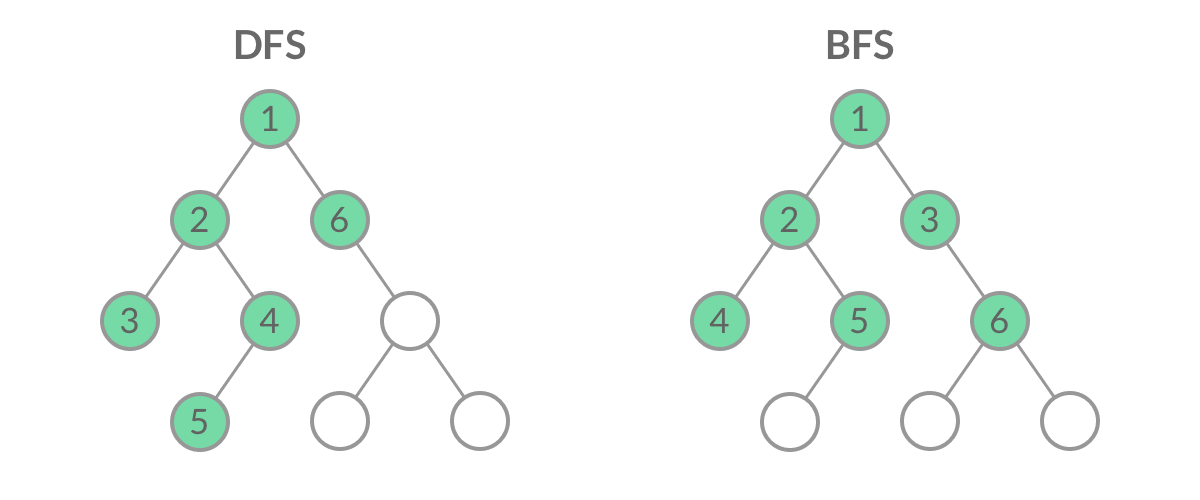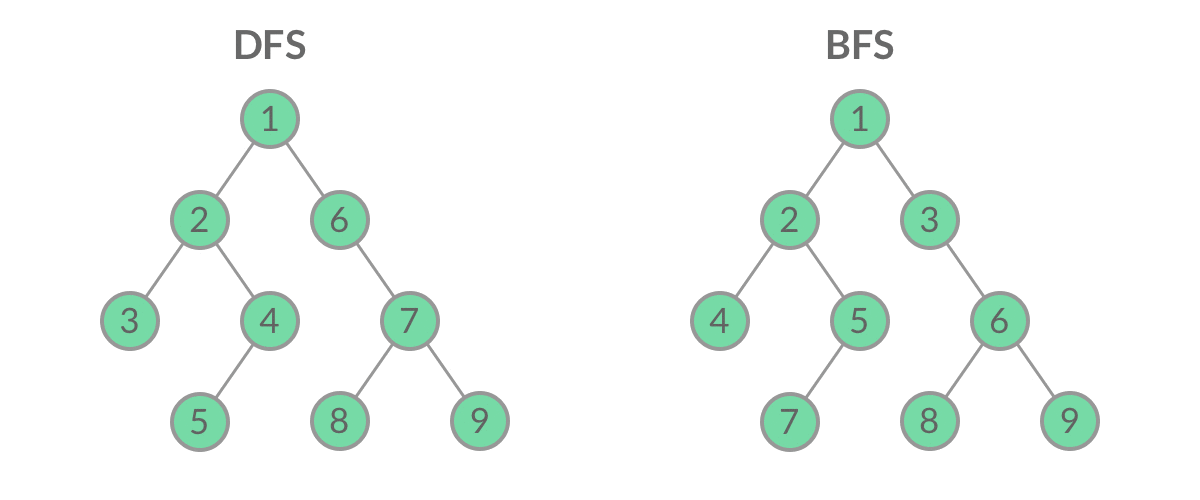
一、了解dfs
1、DFS(Depth First Search)
DFS在我看来就是一条路走到黑,直到无路可走的情况下,才会选择回头,然后重新选择一条路(官方说法即“优先考虑深度”)整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。
2、算法思想
回溯法(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
二、AcWing 842. 排列数字
1.题目
https://www.acwing.com/problem/content/844/

2.dfs 递归过程手动模拟:
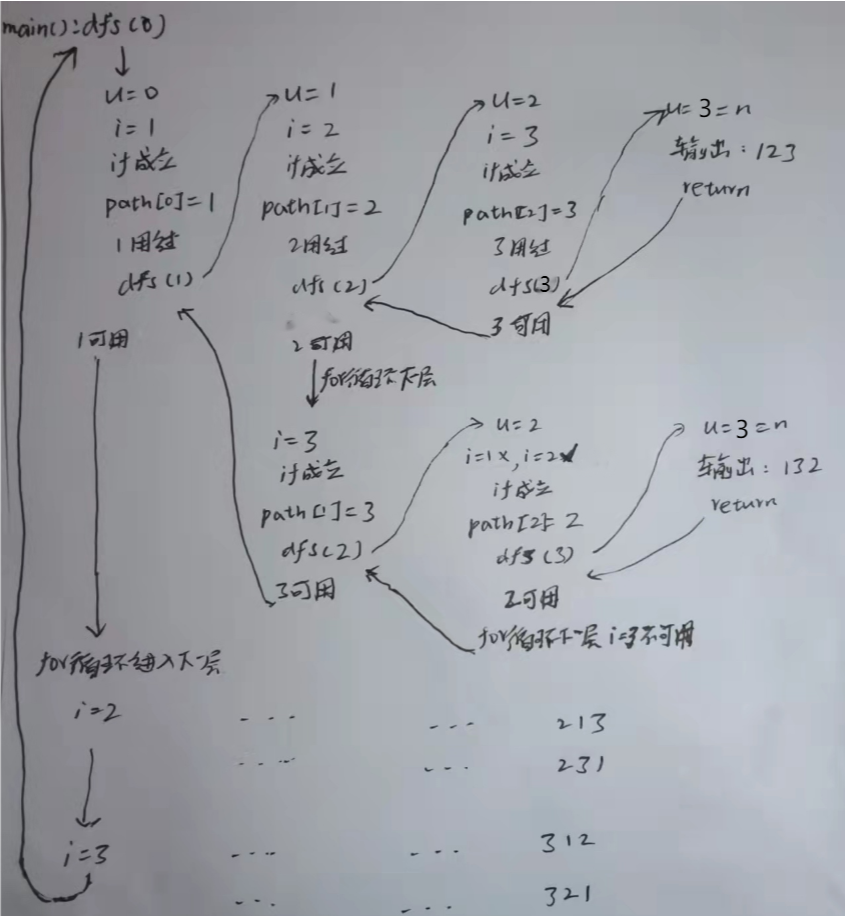
3.代码
public class Main{
static int []path=new int[10];// 从0到n-1共n个位置 存放一个排列
static boolean []sta=new boolean[10];
// 存放每个数字的使用状态 true表示使用了 false表示没使用过
static int n;
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
dfs(0); // 在path[0]处开始填数
}
private static void dfs(int u) {
if(u==n){ // 一个排列填充完成
for (int i = 0; i < n; i++) {
System.out.print(path[i]+" ");
}
System.out.println();
return;
}
for(int i=1;i<=n;i++){
if (!sta[i]) {
path[u]=i; // 把 i 填入数字排列的位置上
sta[i]=true; // 表示该数字用过了 不能再用
dfs(u+1); // 这个位置的数填好 递归到右面一个位置
sta[i]=false; // 恢复现场 该数字后续可用
}
}
}
}
三、AcWing 843. n-皇后问题
1.题目
https://www.acwing.com/problem/content/845/
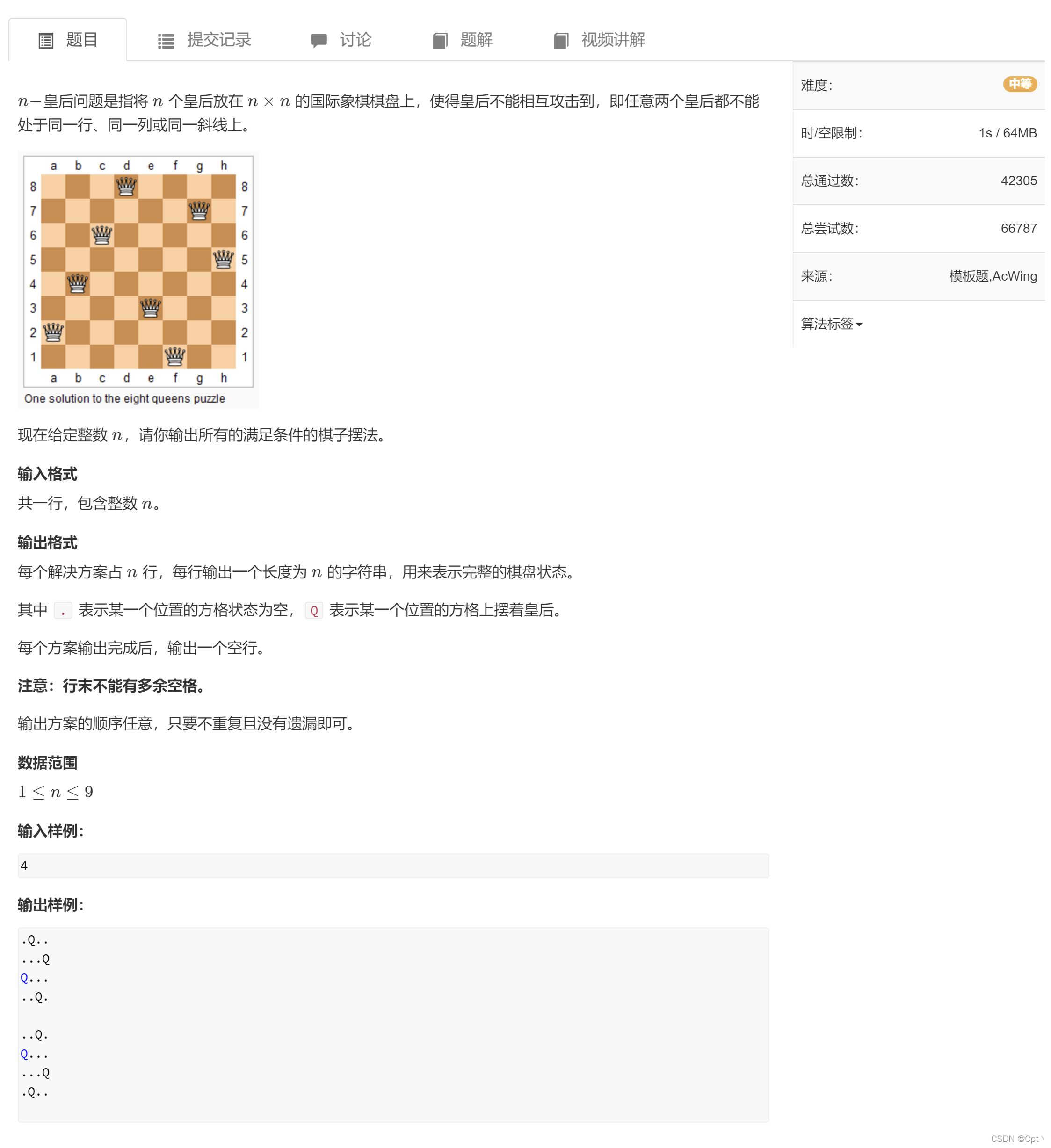
2.思路分析
每一行必定有一个皇后,对行进行深度遍历。
对于第 r 行的第 i 个位置,判断每个点是否可以放皇后,如果可以,则放皇后,然后处理 r + 1 行。
直到 r = n,程序指行完毕。
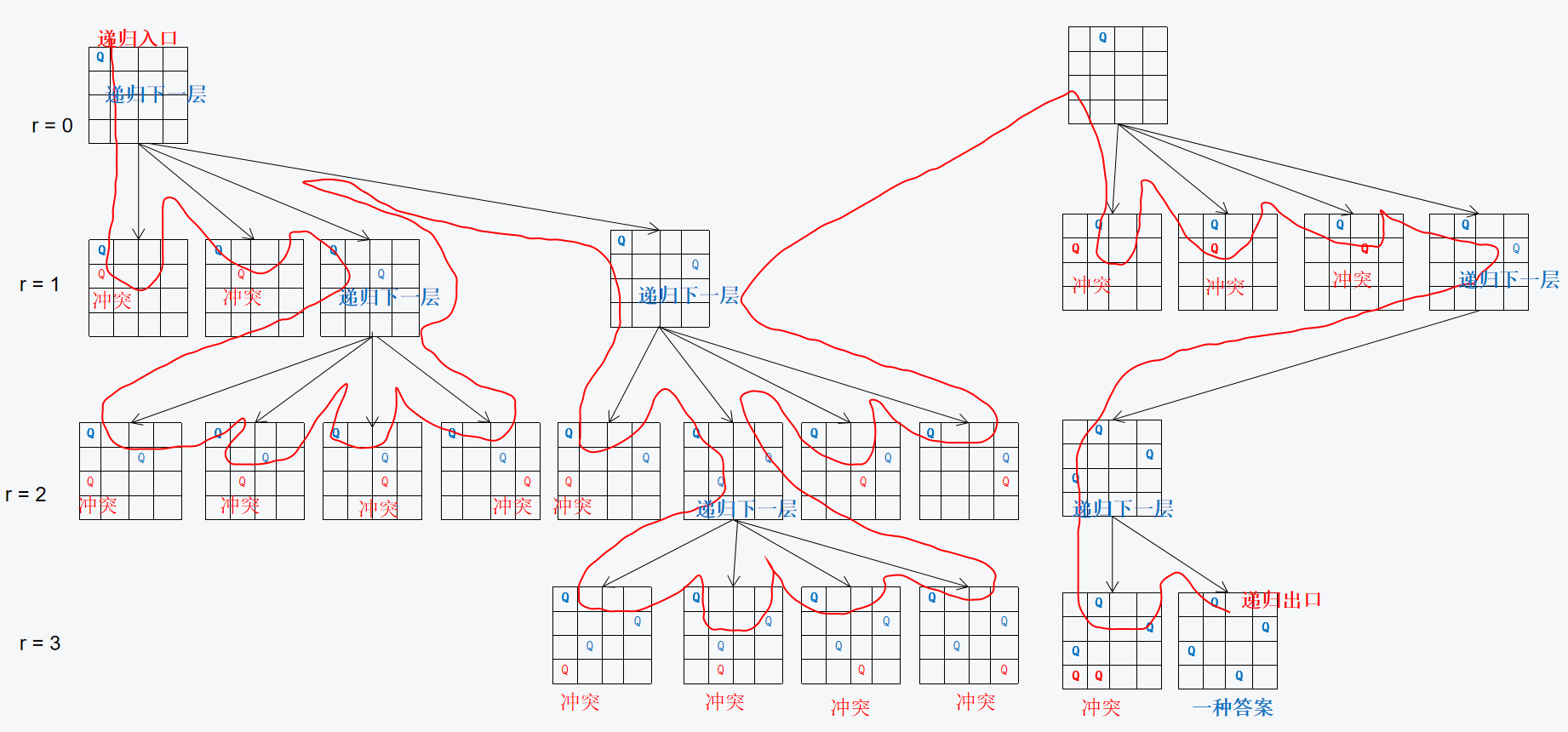
函数名:void dfs(int r): 深度优先遍历函数。参数r:从第r行开始放棋子,处理第r行。
递归结束判定:见代码,当 r == n的时候,说明应该处理第 n行了,也代表第 0~n-1行放好棋子,也就是整个棋盘放好了棋子,也就是得到了一种解,也就是递归结束。
第r行,第i列能不能放棋子:用数组dg udg cor 分别表示:点对应的两个斜线以及列上是否有皇后。
dg[i + r] 表示 r行i列处,所在的对角线上有没有棋子,udg[n - i + r]表示 r行i列处,所在的反对角线上有没有棋子,cor[i]表示第i列上有没有棋子。如果 r行i列的对角线,反对角线上都没有棋子,即!cor[i] && !dg[i + r] && !udg[n - i + r]为真,则代表 r行i列处可以放棋子。
dg[i+r] 和udg[r-i+n]的理解,对角线y1=x1+b1,y2=-x2+b2,如果在不同行,但在同一对角线,经过方程计算得到的截距都是一样的,那么b1=y1-x1,b2=y2+x2,同时为了防止y1-x1是个负数,加上偏移量n
3.代码
import java.util.Scanner;
public class Main{
static int N=11,n;
static char [][]q=new char[N][N]; //存储棋盘
static boolean []cor=new boolean[N]; //判断列是否有皇后
static boolean []dg=new boolean[N*2]; //判断对角线是否有皇后,n * n的矩阵,存在r + i也就是行加上列求截距的操作,必须开两倍大否则就爆了
static boolean []udg=new boolean[N*2]; //判断反对角线是否有皇后
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
q[i][j]='.';
}
}
dfs(0);
}
private static void dfs(int r) {
if(r==n){ //代表棋盘处理完毕,是结束出口
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(q[i][j]);
}
System.out.println();
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) { //第r行,第i列是否可以放皇后
//对角线y1=x1+b1,y2=-x2+b2,那么b1=y1-x1,b2=y2+x2
//为了防止y1-x1是个负数,加上偏移量n
if(!cor[i] &&!dg[i+r] &&!udg[r-i+n]){
q[r][i]='Q';
cor[i]=dg[i+r]=udg[r-i+n]=true;
dfs(r+1); //去下一行遍历
cor[i]=dg[i+r]=udg[r-i+n]=false; //恢复现场
q[r][i]='.';
}
}
}
}感谢你能看完,希望对你有帮助 ,如有错误欢迎指正,码字不易,给个赞呗


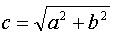


![[future 2022] 基于特征选择的DDoS攻击流分类方法](https://img-blog.csdnimg.cn/img_convert/7532f63af8e7985a520116bcfa825766.jpeg)