问题 B: 2的N次方
题目描述
输入n行,每行一个整数x,输出2的x次方的个位是多少?2的3次方表示3个2相乘,结果是8
输入
输入n行,每行一个整数x
输出
输出n行,每行一个整数,2的x次方的个位。
思路:
找规律,分类讨论.
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int x;
while (std::cin >> x)
{
switch (x % 4)
{
case 1:
std::cout << "2\n";
break;
case 2:
std::cout << "4\n";
break;
case 3:
std::cout << "8\n";
break;
default:
std::cout << "6\n";
break;
}
}
return 0;
}问题 C: 车辆统计
题目描述
结合佛山市的创文活动,文文想做一个关于机动车环保的调查,他来到学校附近的一条主干道,在路边进行观察,并记录下所有经过的摩托车与汽车的车牌。文文用“k+车牌号”的格式记录,其中k=1时代表摩托车,k=2时代表汽车,如“2Y99452”是一辆汽车;车牌号由六个字符组成,如Y99452、E88888等,这个字符串从左边数起的第一个字符为大写英文字母,代表车的归属地,佛山代号有Y、E、X;车牌后面的五位由数字组成。文文在调查后还有大量的数据统计要做,其中之一的任务是:统计各有几辆佛山牌的摩托车和汽车在文文面前经过。你能帮助他吗?
输入
第一行是一个正整数N(1≤N≤10^5),表示共有N个记录。
接下来的N行,每行是一条记录。题目保证给出的车牌不会重复。
输出
输出一行,空格分开的两个整数,分别为属于佛山的摩托车数和汽车数。
样例输入
6 1B45451 2Y54672 1E87680 1X77771 2D23445 1T34567
样例输出
2 1
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::string s;
int n, a = 0, b = 0;
std::cin >> n;
for (int i = 1; i <= n; i++)
{
std::cin >> s;
if (s[1] == 'Y' || s[1] == 'E' || s[1] == 'X')
{
if (s[0] == '1')
{
a++;
}
else
{
b++;
}
}
}
std::cout << a << " " << b;
return 0;
}问题 D: 上学
题目描述
FJ的农场有n个小镇, 奶牛bessi在小镇0,它的学校在小镇n-1. bessi要坐车到学校去上学. N个小镇之间有公交车, bessi就是坐公交车去上学.
小镇之间有m部公交车,我们用(a, b, leave, time, cost) 来描述一部公交车的信息: 表示有一部公交车在时刻leave从小镇a出发, 经过time分钟到达城市b, 车票价格是cost.
由于bessi今天睡过头了,他希望在t分钟以内(包括t分钟)从小镇0到达小镇n-1. 他应该怎样坐公交车才能用最少的车费又能准时上学? 注意: 若bessi在时刻x刚好到达小镇a, 如果公交车的出发时刻也恰好是时刻x, 那么我们规定bessi无法坐到该公交车,也就是说如果想坐这趟公交车则必须在时刻x之前到达小镇a. 当然,有一种情况例外, 小镇0的公交车如果是0时刻出发, bessi在时刻0是可以坐这趟公交车的. 0时刻bessi在小镇0处。
输入
第1行: 三个整数n, t, m,其中2≤n≤50, 1≤m≤50, 1≤t≤ 10^4;
第2至m+1行: 每行五个整数: a, b, leave, time, cost, 描述一部公交车的信息,其中 0≤a≤n-1; 0≤b≤n-1; 0≤leave≤10^4 ; 1≤time≤10^4 ; 1≤cost≤ 10^6。
输出
Bessi至少需要多少车费才能在t分钟内从小镇0到达小镇n-1 ? 如果无法准时到达,输出-1。
样例输入
【样例1】 3 8 2 0 1 0 4 3 1 2 5 3 4 【样例2】 3 7 4 0 1 0 5 1 1 2 6 1 40 0 1 1 2 5 1 2 4 2 5
样例输出
【样例1】 7 【样例2】 10
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
#define ull unsigned long long
const int N = 1e5 + 5;
const int M = 20;
const int INF = 0x3f3f3f;
const ull sed = 31;
const ll mod = 1e9 + 7;
typedef std::pair<int, int> P;
struct node
{
int a, b, lea, tim, cost;
} bus[N];
int n, m, t, ans;
void dfs(int x, int Tm, int retc)
{
if (Tm > t + 1)
return;
if (x == n - 1)
{
ans = std::min(ans, retc);
return;
}
for (int i = 0; i < m; i++)
{
if (bus[i].a != x || bus[i].lea < Tm)
continue;
dfs(bus[i].b, bus[i].lea + bus[i].tim + 1, retc + bus[i].cost);
}
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
ans = INF;
std::cin >> n >> t >> m;
for (int i = 0; i < m; i++)
{
std::cin >> bus[i].a >> bus[i].b >> bus[i].lea >> bus[i].tim >> bus[i].cost;
}
dfs(0, 0, 0);
if (ans == INF)
std::cout << "-1";
else
std::cout << ans;
return 0;
}问题 E: Train
题目大意:
给你两个数字n和i,问从前面数第i个数从后面数是第几个.
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, i;
std::cin >> n >> i;
std::cout << n - i + 1;
return 0;
}问题 F: 栈桥旅游
题目描述
有n名游客在栈桥游玩,现在他们要上船观光。游客编号1到n。船的最大承重为W。第i个人的重量为x[i]。现在有多次游客上下船的操作,请统计一下整个过程中船所承受过的最大总重量是多少,如果该游客想要上船的时候发现船超重了,那么他就不能上船。
输入
第一行输入三个整数n ,m和 W ,分别代表游客数量,上下船的次数,船的最大承重。
接下来n行输入n名游客的重量x[i] 。
接下来m行,每行一个1到n之间的整数,表示游客的编号。表示该游客的上/下船,如果该游客已经在船上,那么该游客就下船,反之就上船。刚开始的时候所有游客都不在船上。
输出
输出近一行1个整数 ,代表船所承受过的最大总重量。
样例输入
5 8 20 5 3 2 2 10 1 2 1 3 1 4 5 1
样例输出
12
提示
30% 1<=n<=10 , m <= 10 , W <= 100
50% 1<=n<=1000 , m <= 1000 , W <= 1e5
100% 1<=n<=100000 , m <= 100000 , W <= 1e9 ,游客的重量w[i] <= 100
思路:
定义变量 res,表示某时刻船的承重。然后 O(N) 遍历,看当前游客能否上船,并同时更新船的最大承重 ans 即可。
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
const int N = 1e5 + 10;
int n, m, w, x[N], vis[N], ans; // vis[i]表示游客i是否在船上
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n >> m >> w;
for (int i = 1; i <= n; i++)
std::cin >> x[i];
int res = 0;
for (int i = 1, inx; i <= m; i++)
{
std::cin >> inx;
if (vis[inx])
{
vis[inx] = 0;
res -= x[inx];
}
else
{
if (res + x[inx] > w)
continue;
vis[inx] = 1;
res += x[inx];
ans = std::max(ans, res);
}
}
std::cout << ans;
return 0;
}问题 G: AcCepted
题目描述
You are given a string S. Each character of S is uppercase or lowercase English letter. Determine if S satisfies all of the following conditions:
The initial character of S is an uppercase A.
There is exactly one occurrence of C between the third character from the beginning and the second to last character (inclusive).
All letters except the A and C mentioned above are lowercase.
Constraints
4≤|S|≤10 (|S| is the length of the string S.)
Each character of S is uppercase or lowercase English letter.
输入
Input is given from Standard Input in the following format:
S
输出
If S satisfies all of the conditions in the problem statement, print AC; otherwise, print WA.
样例输入
AtCoder
样例输出
AC
提示
The first letter is A, the third letter is C and the remaining letters are all lowercase, so all the conditions are satisfied.
思路:
首先考虑除了A,C外,是否还有大写字母,如果有,则排除这种情况
二是寻找C存在的位置,根据题目已知它是在第三个字符和倒数第二个字符之间的(包含第三和倒数第二个字符)并且次数只能是1,所以这里用了一个count来计数,再判断第一个字符是否是A,就全面考虑了。
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
int n1, t;
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::string c;
int len, f = 1;
std::cin >> c;
for (int i = 0; c[i]; i++)
{
if (c[i] != 'A' && c[i] != 'C')
if (isupper(c[i]))
f = 0;
}
int count = 0;
for (int i = 2; i < c.size() - 1; i++)
if (c[i] == 'C')
count++;
if (count != 1)
f = 0;
if (c[0] != 'A')
f = 0;
if (f == 1)
std::cout << "AC";
else
std::cout << "WA";
return 0;
}问题 H: We Love ABC
题目描述
The ABC number of a string T is the number of triples of integers (i,j,k) that satisfy all of the following conditions:
- 1≤i<j<k≤T| (|T| is the length of T.)
- Ti= A (Ti is the i-th character of T from the beginning.)
- Tj= B
- Tk= C
For example, when T= ABCBC, there are three triples of integers (i,j,k) that satisfy the conditions: (1,2,3),(1,2,5),(1,4,5). Thus, the ABC number of T is 3.
You are given a string S. Each character of S is A, B, C or ?.
Let Q be the number of occurrences of ? in S. We can make 3Q strings by replacing each occurrence of ? in S with A, B or C. Find the sum of the ABC numbers of all these strings.
This sum can be extremely large, so print the sum modulo 10^9+7.
Constraints
3≤|S|≤105
Each character of S is A, B, C or ?.
输入
Input is given from Standard Input in the following format:
S
输出
Print the sum of the ABC numbers of all the 3Q strings, modulo 109+7.
样例输入
A??C
样例输出
8
提示
In this case, Q=2, and we can make 3Q=9 strings by by replacing each occurrence of ? with A, B or C. The ABC number of each of these strings is as follows:
AAAC: 0
AABC: 2
AACC: 0
ABAC: 1
ABBC: 2
ABCC: 2
ACAC: 0
ACBC: 1
ACCC: 0
The sum of these is 0+2+0+1+2+2+0+1+0=8, so we print 8 modulo 10^9+7, that is, 8.
思路:
给一个只含 A B C ? 四种字符的串,其中 ? 可以匹配任意字母,问能形成多少个子序列 ABC。
先不考虑问号,在只有字母的情况下很容易想到动态规划:dp[i][j] 表示前 i 个字符形成长度为 j 的子序列,直接从 i −1 转移就行了。然后考虑问号的影响,问号相当于三种字母随便填,所以即便问号这一位不用于答案的子序列中,也会使上一个状态的贡献翻上三倍;如果这一位在子序列里用到了,那就相当于三种字母各转移一次。在之前的 dp 上稍作修改即可。
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
const int maxn = 1e5 + 5;
const ll modulo = 1e9 + 7;
ll dp[maxn][4];
char s[maxn];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> (s + 1);
int n = strlen(s + 1);
dp[0][0] = 1;
for (int i = 1; i <= n; ++i)
{
if (s[i] == '?')
{
for (int j = 0; j <= 3; ++j)
dp[i][j] = dp[i - 1][j] * 3 % modulo;
dp[i][1] = (dp[i][1] + dp[i - 1][0]) % modulo;
dp[i][2] = (dp[i][2] + dp[i - 1][1]) % modulo;
dp[i][3] = (dp[i][3] + dp[i - 1][2]) % modulo;
}
else
{
for (int j = 0; j <= 3; ++j)
dp[i][j] = dp[i - 1][j];
if (s[i] == 'A')
dp[i][1] = (dp[i][1] + dp[i - 1][0]) % modulo;
else if (s[i] == 'B')
dp[i][2] = (dp[i][2] + dp[i - 1][1]) % modulo;
else
dp[i][3] = (dp[i][3] + dp[i - 1][2]) % modulo;
}
}
std::cout << dp[n][3];
return 0;
}问题 I: Grid Compression
题目描述
There is a grid of squares with H horizontal rows and W vertical columns. The square at the i-th row from the top and the j-th column from the left is represented as (i,j). Each square is black or white. The color of the square is given as an H-by-W matrix (ai,j). If ai,j is ‘.‘, the square (i,j) is white; if ai,j is '#', the square (i,j) is black.
Snuke is compressing this grid. He will do so by repeatedly performing the following operation while there is a row or column that consists only of white squares:
Operation: choose any one row or column that consists only of white squares, remove it and delete the space between the rows or columns.
It can be shown that the final state of the grid is uniquely determined regardless of what row or column is chosen in each operation. Find the final state of the grid.
Constraints
1≤H,W≤100
ai,j is '.' or '#'.
There is at least one black square in the whole grid.
输入
Input is given from Standard Input in the following format:
H W
a1,1…a1,W
:
aH,1…aH,W
输出
Print the final state of the grid in the same format as input (without the numbers of rows and columns); see the samples for clarity.
样例输入
4 4 ##.# .... ##.# .#.#
样例输出
### ### .##
思路:
开两个bool数组记录当前这一行(或列)是否全为‘.’,输出时进行判断
注意这一行啥都没输出时不要换行
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
std::string s[110], ans[110];
bool hang[110], lie[110];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int h, w, i, j;
std::cin >> h >> w;
for (i = 0; i < h; i++)
std::cin >> s[i];
memset(hang, 1, sizeof(hang));
memset(lie, 1, sizeof(lie));
for (i = 0; i < h; i++)
{
bool all = 1;
for (j = 0; j < w; j++)
if (s[i][j] == '#')
{
all = 0;
break;
}
if (all)
hang[i] = 0;
}
for (i = 0; i < w; i++)
{
bool all = 1;
for (j = 0; j < h; j++)
if (s[j][i] == '#')
{
all = 0;
break;
}
if (all)
lie[i] = 0;
}
for (i = 0; i < h; i++)
{
bool out = 0;
for (j = 0; j < w; j++)
if ((hang[i]) && (lie[j]))
{
std::cout << s[i][j];
out = 1;
}
if (out)
std::cout << '\n';
}
return 0;
}问题 J: 分享奖品
题目描述
在学校创文知识竞赛中,明明和文文总共获得了n(1≤ n≤250)件奖品,每件奖品都有一个价值Vi (1 ≤ Vi ≤ 2,000)。他们想按价值平均分享这些奖品,假如不能平均分就尽量让它们的差距最小。现在给出奖品数及它们的价值,明明想算出划分后的最小差值,以及划分的方案数。
例如:有5件奖品价值分别是:2, 1,8, 4, 16。明明和文文分为两部分,分别是前面四个为一部分1+2+4+8=15,16为单独一部分,那么两部分相差:16-15 = 1。这个是差距最小的划分方案,并且这种方案的划分方法只有1种。
相同价值的奖品相交换算不同的方案,如:有四件奖品价值分别为{1, 1, 1, 1},有6种不同的划分方案,使这些奖品分为两部分,每一部分2个奖品。
输入
第一行:一个整数n(1≤n≤250);
接着有n行,每行一个整数Vi (1 ≤ Vi ≤ 2,000)代表每件奖品的价值。
输出
第一行:一个整数,代表划分的两部分的最小差值。
第二行:一个整数,代表最小差值的划分方案数,结果对1,000,000求余(mod 1,000,000)。
样例输入
【样例1】 5 2 1 8 4 16 【样例2】 1 1
样例输出
【样例1】 4 1 1 1 1 【样例2】 0 6
思路:
首先可以用动态规划的思想:
设 f[i][j] 为前i件奖品他们价值为j的不同方案
那么状态转移方程就是:
f[i][j] = f[i-1][j]+f[i-1][j-a[i]]
这时写的代码是这样的:
#include<bits/stdc++.h>
using namespace std;
const int MOD = 1000000;
const int N = 300;
int n,a[N],f[N][2000*N];
int maxn = 0;
int main(){
cin >> n;
for(int i=1;i<=n;i++)cin >> a[i],maxn+=a[i];
f[0][0] = 1;
for(int i=1;i<=n;i++){
for(int j=0;j<=maxn;j++){
f[i][j] = (f[i-1][j]+f[i-1][j-a[i]])%MOD;
}
}
int ans=2000*N,cnt=-1;
for(int j=0;j<=maxn;j++){
if(abs((maxn-j)-j)<ans){
ans = abs((maxn-j)-j);
cnt = f[n][j];
}
}
cout << ans << endl << cnt << endl;
return 0;
}结果: MLE
这个代码的空间复杂度太高了。于是我把f的第一维改成了滚动数组:
#include<bits/stdc++.h>
using namespace std;
const int MOD = 1000000;
const int N = 260;
int n,a[N],f[3][2000*N];
bool vis[3][2000*N];
int maxn = 0;
int main(){
cin >> n;
for(int i=1;i<=n;i++)cin >> a[i],maxn+=a[i];
f[0][0] = 1;
vis[0][0] = 1;
for(int i=1;i<=n;i++){
for(int j=0;j<=maxn;j++){
if(j-a[i]>=0){
f[i%2][j] = (f[(i-1)%2][j]+f[(i-1)%2][j-a[i]])%MOD;
vis[i%2][j]= vis[(i-1)%2][j] || vis[(i-1)%2][j-a[i]];
}
else{
f[i%2][j] = f[(i-1)%2][j];
vis[i%2][j] = vis[(i-1)%2][j];
}
}
}
int ans=2000*N,cnt=-1;
for(int j=0;j<=maxn;j++){
if(abs((maxn-j)-j)<ans and vis[n%2][j]!=0){
ans = abs((maxn-j)-j);
cnt = f[n%2][j];
}
}
cout << ans << endl << cnt << endl;
return 0;
}这次又变成了TLE
再向时间优化,将 mod 的次数变少然后把vis数组加上(就是记录能否走到这个点的数组)最终的答案是:
#include<bits/stdc++.h>
using namespace std;
const int MOD = 1000000;
const int N = 260;
int n,a[N],sum[N],f[3][2000*N];
bool vis[3][2000*N];
int maxn = 0;
int main(){
cin >> n;
for(int i=1;i<=n;i++){
cin >> a[i];
maxn+=a[i];
sum[i]=sum[i-1]+a[i];
}
f[0][0] = 1;
vis[0][0] = 1;
for(int i=1;i<=n;i++){
int I2=i%2,I12=(i-1)%2;
for(int j=0;j<=sum[i];j++){
if(j-a[i]>=0){
f[I2][j] = f[I12][j]+f[I12][j-a[i]];
if(f[I2][j]>=MOD) f[I2][j]-=MOD;
vis[I2][j]= vis[I12][j] || vis[I12][j-a[i]];
}
else{
f[I2][j] = f[I12][j];
vis[I2][j] = vis[I12][j];
}
}
}
int ans=2000*N,cnt=-1;
for(int j=0;j<=maxn;j++){
if(abs((maxn-j)-j)<ans and vis[n%2][j]!=0){
ans = abs((maxn-j)-j);
cnt = f[n%2][j];
}
}
cout << ans << endl << cnt << endl;
return 0;
}问题 L: 巧克力
题目描述
在一个二维平面里,有n块巧克力,每块巧克力都是长方形(正方形也可以认为是长方形),每块巧克力的四条边都平行于X轴或平行于Y轴。我们用(X1, Y1, X2, Y2)来描述一块巧克力的所在位置,其中(X1, Y1)表示这块巧克力左下角的坐标,(X2,Y2) 表示这块巧克力右上角的坐标。注意:题目给出的n块巧克力之间可能有重叠的地方。奶牛bessie手头上有一个a×b的长方形铁丝框。 Bessie想知道它应该把铁丝框放在哪个位置,才能使得可以拿走的巧克力的个数最多?农夫FJ规定:bessie铁丝框放的位置也必须要平行X轴和Y轴,而且还规定,bessie只能拿走在铁丝框里面的巧克力,bessie最多能拿走多少块巧克力?bessie只能放一次铁丝框。解释:如果某块巧克力的位置是:(1,1, 2, 2), 而铁丝框的位置是(-1,1,2,100), 那么这块巧克力也是在铁丝框里面,可以被bessie拿走。也就是说,如果某块巧克力任何部分都没有超出铁丝框, 就可以认为是在铁丝框里面。
输入
第1行:一个整数n,其中0≤n≤50。
第2至n+1行,每行四个整数: X1, Y1, X2, Y2, 描述巧克力的位置,
其中 -10^9≤X1≤10^9 , -10^9≤Y1≤ 10^9, -10^9≤X2≤ 10^9, -10^9≤Y2≤10^9。
最后一行:两个整数a和b, 且1≤a≤10^9 ,1≤b≤10^9 。
输出
一个整数,bessie最多能拿走多少块巧克力?
样例输入
【样例1】 3 1 1 2 2 2 2 3 3 3 3 4 4 2 2 【样例2】 2 0 1 2 3 3 0 4 2 4 3
样例输出
【样例1】 2 【样例2】 2
提示
样例1解释:如果bessie把铁丝框放在(1,1,3,3)处, 那么它可以拿走第1和第2块巧克力;如果把铁丝框放在(2,2,4,4)那么它可以拿走第2和第3块巧克力。
思路:
直接按题目要求的做就可以了。
首先要明白每个框最好的放法肯定是贴着某(些)巧克力两条的边。
然后我们只需将所有巧克力的边收集起来然后枚举矩形框的位置,判断巧克力是否入框就行了。
值得注意的,框可以翻来覆去放。
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
#define N 60
int n, A, B, px[N << 1], py[N << 1], ans;
struct Data
{
int x1, y1, x2, y2;
Data() {}
Data(int x1, int y1, int x2, int y2) : x1(x1), y1(y1), x2(x2), y2(y2) {}
} rec[N];
bool Judge(Data P, Data Q)
{
return P.x1 >= Q.x1 && P.y1 >= Q.y1 && P.x2 <= Q.x2 && P.y2 <= Q.y2;
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n;
for (int i = 1; i <= n; i++)
{
std::cin >> rec[i].x1 >> rec[i].y1 >> rec[i].x2 >> rec[i].y2;
px[++px[0]] = rec[i].x1;
px[++px[0]] = rec[i].x2;
py[++py[0]] = rec[i].y1;
py[++py[0]] = rec[i].y2;
}
std::cin >> A >> B;
for (int i = 1; i <= px[0]; i++)
for (int j = 1; j <= py[0]; j++)
{
Data Fe1 = Data(px[i], py[j], px[i] + A, py[j] + B);
Data Fe2 = Data(px[i], py[j], px[i] + B, py[j] + A);
int temp1 = 0, temp2 = 0;
for (int k = 1; k <= n; k++)
{
if (Judge(rec[k], Fe1))
temp1++;
if (Judge(rec[k], Fe2))
temp2++;
}
ans = std::max(ans, std::max(temp1, temp2));
}
std::cout << ans;
return 0;
}问题 M: Median of Medians
题目描述
We will define the median of a sequence b of length M, as follows:
Let b' be the sequence obtained by sorting b in non-decreasing order. Then, the value of the (M⁄2+1)-th element of b' is the median of b. Here, ⁄ is integer division, rounding down.
For example, the median of (10,30,20) is 20; the median of (10,30,20,40) is 30; the median of (10,10,10,20,30) is 10.
Snuke comes up with the following problem.
You are given a sequence a of length N. For each pair (l,r) (1≤l≤r≤N), let ml,r be the median of the contiguous subsequence (al,al+1,…,ar) of a. We will list ml,r for all pairs (l,r) to create a new sequence m. Find the median of m.
Constraints
1≤N≤105
ai is an integer.
1≤ai≤109
输入
Input is given from Standard Input in the following format:
N
a1 a2 … aN
输出
Print the median of m.
样例输入
3 10 30 20
样例输出
30
提示
The median of each contiguous subsequence of a is as follows:
The median of (10) is 10.
The median of (30) is 30.
The median of (20) is 20.
The median of (10,30) is 30.
The median of (30,20) is 30.
The median of (10,30,20) is 20.
Thus, m=(10,30,20,30,30,20) and the median of m is 30.
思路:
大意:定义中位数是一个序列从小到大的第(n/2+1)项(取下整),现给定一个长度为n的序列,对于任意的l,r(1<=l<=r<=n),将这一段数的中位数放入一个新的序列中,求这个新序列的中位数
题解:一看分值A+B+C<D,就有种不详的预感
首先明确,这样的子序列一共只有n(n+1)/2个,因此答案就是在新序列排序后处在n(n+1)/2/2+1的位置上的数
考虑到n很大所以用二分答案
考虑到这里至于数之间的大小关系有关所以离散
那么如何判断我们二分出的答案是否合法呢?
我们回到开头,想要找到出现在这个位置上的数,我们可以统计在新序列中有多少个元素大于等于它就行了
那么怎么处理这个呢?
假设我们当前枚举的数为x,我们还是注意到这里至于数之间的大小关系有关,所以我们可以原序列中比x大或相等的数记为1,比x小的记为-1,得到一个由1与-1组成的序列
此时,l到r之间的中位数大于等于x 也就等价于 得到的新序列(由1与-1组成)中l到r这一段区间中元素和>=0
用前缀和的方式求区间和,可将问题转化成:对于l,r,找到满足Sl-1<=Sr的数对数量
等等,这不就是求逆序对嘛.
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
const ll maxn = 1e5+5;
ll n;
ll pre[maxn];
ll c[maxn<<1], s[maxn];
ll lowbit(ll x) {return x&(-x);}
ll query(ll x){
ll res = 0;
for(ll i = x; i ; i -= lowbit(i)){
res += c[i];
}
return res;
}
void add(ll x){
for(ll i = x; i <= 2*n; i += lowbit(i)){
c[i] += 1;
}
}
bool check(ll x){
memset(c, 0, sizeof(c));
s[0] = 0;
for(ll i = 1; i <= n; i++) {
s[i] = pre[i]>=x?1:-1;
s[i] += s[i-1];
}
ll sum = 0;
for(ll i = 0; i <= n; i++){
sum += query(s[i]+n);
add(s[i]+n);
}
ll num = n*(n+1)/2, ss;
if (num%2) ss = (num+1)/2;
else ss = num/2;
if (sum >= ss) return true;
return false;
}
int main ()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n;
ll l = 1, r = 1;
for(ll i = 1; i <= n; i++) {
std::cin >> pre[i];
if (pre[i] > r) r = pre[i];
}
ll ans;
while(l <= r){
ll mid = (l+r)>>1;
if (check(mid)) ans = mid, l = mid+1;
else r = mid-1;
}
std::cout << ans;
return 0;
}问题 N: 愧疚指数
题目描述
佛山创文要求大家要遵守交通规则,发扬尊老爱幼精神。文文想做一个关于公交文化的调查。他专门为排队上车发明了一套叫做“愧疚指数”的分析系统,就是在队列中把人分为三等:第一等为优先级最高,最需要照顾的老人、小孩、孕妇等,应该最优先上车,优先代号为1;第二等是普通女人,为了发扬绅士风度,男人是要让女人先上车的,但优先级低于一等,优先代号为2;第三等是普通男人,优先级最低,应该排在最后面,优先代号为3。所谓的“愧疚指数”是指队列中一个人后面有多少人的优先级比他高,如队列中有5个人分别为:3 2 1 2 1,那么这5个人的“愧疚指数”分别为:4 2 0 1 0。现在已经知道一个队列,请你帮文文算出队列中每个人的“愧疚指数”。
输入
第一行是一个正整数n,表示一共有多少个人排队。
第二行有n个用空格隔开的正整数,它们从左至右给出了队列中n个人的优先代号。
输出
输出一行:有n个用空格分开的正整数,代表队列中每个人的“愧疚指数”。
样例输入
5 3 2 1 2 1
样例输出
4 2 0 1 0
提示
对于80%的数据,n≤10000;
对于100%的数据,n≤200000。
思路:
用前缀和数组记录一下前i个人中优先代号为1和2的人数.
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
const int maxn = 2e5 + 10;
int first[maxn], second[maxn];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n;
std::cin >> n;
std::vector<int> a(n + 1);
for (int i = 1; i <= n; i++)
std::cin >> a[i];
if (a[1] == 1)
first[1] = 1;
else if (a[1] == 2)
second[1] = 1;
for (int i = 2; i <= n; i++)
first[i] = first[i - 1] + (a[i] == 1), second[i] = second[i - 1] + (a[i] == 2);
for (int i = 1; i <= n; i++)
{
if (a[i] == 3)
std::cout << first[n] - first[i - 1] + second[n] - second[i - 1] << ' ';
else if (a[i] == 2)
std::cout << first[n] - first[i - 1] << ' ';
else
std::cout << '0' << ' ';
}
return 0;
}问题 O: Rated for Me
题目描述
A programming competition site AtCode regularly holds programming contests.
The next contest on AtCode is called ABC, which is rated for contestants with ratings less than 1200.
The contest after the ABC is called ARC, which is rated for contestants with ratings less than 2800.
The contest after the ARC is called AGC, which is rated for all contestants.
Takahashi's rating on AtCode is R. What is the next contest rated for him?
Constraints
0≤R≤4208
R is an integer.
输入
Input is given from Standard Input in the following format:
R
输出
Print the name of the next contest rated for Takahashi (ABC, ARC or AGC).
样例输入
1199
样例输出
ABC
思路:
直接分类讨论即可.
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int rate;
std::cin >> rate;
if (rate < 1200)
std::cout << "ABC";
else if (rate >= 1200 && rate < 2800)
std::cout << "ARC";
else
std::cout << "AGC";
return 0;
}问题 P: All Green
题目描述
A programming competition site AtCode provides algorithmic problems. Each problem is allocated a score based on its difficulty. Currently, for each integer i between 1 and D (inclusive), there are pi problems with a score of 100i points. These p1+…+pD problems are all of the problems available on AtCode.
A user of AtCode has a value called total score. The total score of a user is the sum of the following two elements:
base score: the sum of the scores of all problems solved by the user.
Perfect bonuses: when a user solves all problems with a score of 100i points, he/she earns the perfect bonus of ci points, aside from the base score (1≤i≤D).
Takahashi, who is the new user of AtCode, has not solved any problem. His objective is to have a total score of G or more points. At least how many problems does he need to solve for this objective?
Constraints
1≤D≤10
1≤pi≤100
100≤ci≤106
100≤G
All values in input are integers.
ci and G are all multiples of 100.
It is possible to have a total score of G or more points.
输入
Input is given from Standard Input in the following format:
D G
p1 c1
:
pD cD
输出
Print the minimum number of problems that needs to be solved in order to have a total score of G or more points. Note that this objective is always achievable (see Constraints).
样例输入
2 700 3 500 5 800
样例输出
3
提示
In this case, there are three problems each with 100 points and five problems each with 200 points. The perfect bonus for solving all the 100-point problems is 500 points, and the perfect bonus for solving all the 200-point problems is 800 points. Takahashi's objective is to have a total score of 700 points or more.
One way to achieve this objective is to solve four 200-point problems and earn a base score of 800 points. However, if we solve three 100-point problems, we can earn the perfect bonus of 500 points in addition to the base score of 300 points, for a total score of 800 points, and we can achieve the objective with fewer problems.
思路:
因为最多只有10个题目,那我们可以先暴力每个题目做与不做,就是2^10,如果有剩下的分数,你就可以用
贪心,倒着取题目,来做,然后对于每次的题目数取个min
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
const int maxn = 200;
int d, gg, c[maxn], p[maxn], vis[maxn];
struct node
{
int c, p;
int id, s;
} g[maxn];
int getans()
{
int ans = 0;
int sum = 0;
int G = gg;
for (int i = 1; i <= d; i++)
{
if (vis[i])
G -= (g[i].p * 100 * i + g[i].c), ans += g[i].p;
}
for (int i = d; i >= 1; i--)
{
if (!vis[i])
{
if (G > 0)
{
if (G >= g[i].p * 100 * i)
{
ans += g[i].p;
G -= (g[i].p * 100 * i + g[i].c);
}
else
{
ans += G / (i * 100);
G -= 100 * i * (G / (i * 100));
}
}
}
}
if (G <= 0)
return ans;
else
return 1e9;
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
while (std::cin >> d >> gg)
{
int ans = 1e9;
for (int i = 1; i <= d; i++)
std::cin >> g[i].p >> g[i].c, g[i].id = i;
for (int i = 0; i < (1 << d); i++)
{
for (int j = 1; j <= d; j++)
{
if (1 & (i >> (j - 1)))
vis[j] = 1;
else
vis[j] = 0;
}
int sum = getans();
ans = std::min(ans, sum);
}
std::cout << ans << std::endl;
}
return 0;
}问题 Q: 世界语
题目描述
有一种世界流行的语言叫“Esperanto”, 在该语言中, 数字1 至 10分别是: "unu", "du", "tri", "kvar", "kvin", "ses", "sep", "ok", "nau", "dek";数字11至19分别是: "dek unu", "dek du", ..., "dek nau" ,也就是一个 "dek"后面一个空格,接着是个位上的数字;数字20至29分别是: "dudek", "dudek unu", "dudek du", ..., "dudek nau"; 相似的, 30 是"tridek", ..., 90 是"naudek" 。 给你一个整数x, 输出它的Esperanto 表示法。
输入
输入一个整数x,其中1≤x≤99 。
输出
整数x的Esperanto表示法.
样例输入
31
样例输出
tridek unu
思路:
模拟一下即可.
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::map<int, std::string> mp;
mp[1] = "unu";
mp[2] = "du";
mp[3] = "tri";
mp[4] = "kvar";
mp[5] = "kvin";
mp[6] = "ses";
mp[7] = "sep";
mp[8] = "ok";
mp[9] = "nau";
mp[10] = "dek";
std::string s;
std::cin >> s;
if (s.size() == 1)
std::cout << mp[s[0] - '0'];
else if (s.size() == 2)
{
if (s[0] == '1' && s[1] == '0')
std::cout << mp[10];
else if (s[0] == '1' && s[1] != '0')
std::cout << mp[10] << ' ' << mp[s[1] - '0'];
else if (s[0] != '1' && s[1] == '0')
std::cout << mp[s[0] - '0'] << mp[10];
else
std::cout << mp[s[0] - '0'] << mp[10] << ' ' << mp[s[1] - '0'];
}
return 0;
}问题 R: 投喂修狗
题目描述
小明家里有n只修狗,小明想投喂一下这些修狗,要保证每只狗都被喂过,于是让它们在客厅里面站成一排。每只修狗都有它的体积v,一般体积越大的修狗吃的粮食越多,同时修狗比较喜欢妒忌,它们会注意到自己左边第一只和右边第一只同伴的体积和被投喂的狗粮的数量,如果存在体积比自己瘦小还吃得不比自己少的它就会开始大吵大闹,小明不希望看到这样的情况发生,同时小明也想尽可能的节约一点狗粮,那么请你帮忙计算一下需要的最少狗粮是多少。
输入
第一行一个整数N,表示修狗的数量;
第二行N个数表示修狗的体积,以空格隔开
输出
输出一个数,表示最少所需的狗粮数。
样例输入
3 1 2 2
样例输出
4
提示
对于20%的数据,0<N≤10;
对于50%的数据,0<N≤1000;
对于100%的数据,0<N≤50000 ,v[i] <= 50000。
思路:
想象成一排各有高度的连绵的山群,我们先找到“谷底”,即体重的都比左右邻居小的狗,各以它们为起点向左向右遍历计算各只狗吃的狗粮数。第一次遍历完后仍有部分区间没有被计算,如以两山峰为左右端点且中间没有谷底的区间,记录这些区间,并进行第二次遍历,计算答案。
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
const int N = 5e4 + 10;
int n, a[N], ans, b[N];
std::vector<int> s;
struct node
{
int l, r;
} m[N];
// 数组m[]统计第一次遍历没有被遍历到的区间
// 数组a[i]记录i修狗的体重,数组b[i]记录i修狗吃的狗粮数
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n;
for (int i = 1; i <= n; i++)
std::cin >> a[i];
// 记录“谷底”
if (a[1] < a[2])
s.push_back(1);
for (int i = 2; i < n; i++)
if (a[i] < a[i - 1] && a[i] < a[i + 1])
s.push_back(i);
if (a[n] < a[n - 1])
s.push_back(n);
// 从每个“谷底”开始,向左向右遍历,计算答案
for (int i = 0; i < s.size(); i++)
{
int beg = s[i];
b[beg] = 1;
// 取max的原因是防止“山头”两侧深度不一样
for (int j = beg + 1; a[j] > a[j - 1] && j <= n; j++)
b[j] = std::max(b[j], b[j - 1] + 1);
for (int j = beg - 1; a[j] > a[j + 1] && j >= 1; j--)
b[j] = std::max(b[j], b[j + 1] + 1);
}
// 记录区间
int i, tot = 0;
for (i = 1; i <= n; i++)
{
if (!b[i])
{
tot++;
m[tot].l = i;
int j;
for (j = i + 1; !b[j] && j <= n; j++)
;
m[tot].r = j - 1;
i = m[tot].r;
}
}
// 第二次遍历
// Eg:1 2 3 3 3 4 5 4 3 3 3 2 1
for (int i = 1; i <= tot; i++)
{
for (int j = m[i].l; j <= m[i].r; j++)
{
if (a[j] == a[j - 1])
{
if (a[j] == a[j + 1] || a[j] < a[j + 1])
b[j] = 1;
}
if (a[j] > a[j - 1])
b[j] = b[j - 1] + 1;
}
for (int j = m[i].r; j >= m[i].l; j--)
{
if (b[j])
continue;
if (a[j] == a[j + 1])
b[j] = 1;
if (a[j] > a[j + 1])
b[j] = std::max(b[j], b[j + 1] + 1);
}
}
for (int i = 1; i <= n; i++)
ans += b[i];
std::cout << ans;
return 0;
}问题 S: 连续自然数的和
题目描述
输入n和k两个整数,然后输入n个数,组成一个序列,请你帮忙找出在这个序列中共有多少组连续的数的和是k
输入
第一行2个整数 n和k,中间有一个空格间隔
第二行输入n个整数,每个数中间有一个空格
输出
一行一个整数
样例输入
5 8 1 3 2 2 6
样例输出
2
提示
30% 1<=n<=1000; 序列中第i个数的值a[i]满足0<=a[i]<=1e5; 0<=k<=1e9
50% 1<=n<=10000; 序列中第i个数的值a[i]满足0<=a[i]<=1e9; 0<=k<=1e9
100% 1<=n<=100000; 序列中第i个数的值a[i]满足0<=a[i]<=1e9; 0<=k<=1e9
思路:
计算前缀和数组 sum[],并统计每个 sum[i] 出现的次数。依题意可得 sum[R]-sum[L-1]=k,调换式子两边,有 sum[R]-k=sum[L-1],所以可以枚举每一个 R,然后累计对应的 sum[L-1] 出现的次数。
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
#define inf 0x3f3f3f3f
const int N = 1e5 + 10;
int n, k, a[N], sum[N];
std::map<int, int> mp;
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n >> k;
for (int i = 1; i <= n; i++)
std::cin >> a[i];
mp[0] = 1;
for (int i = 1; i <= n; i++)
{
sum[i] = sum[i - 1] + a[i];
mp[sum[i]]++;
}
int ans = 0;
for (int i = n; i >= 1; i--)
if (mp[sum[i] - k])
ans += mp[sum[i] - k];
std::cout << ans;
return 0;
}问题 T: Candles
题目描述
There are N candles placed on a number line. The i-th candle from the left is placed on coordinate xi. Here, x1<x2<…<xN holds.
Initially, no candles are burning. Snuke decides to light K of the N candles.
Now, he is at coordinate 0. He can move left and right along the line with speed 1. He can also light a candle when he is at the same position as the candle, in negligible time.
Find the minimum time required to light K candles.
Constraints
1≤N≤105
1≤K≤N
xi is an integer.
|xi|≤108
x1<x2<…<xN
输入
Input is given from Standard Input in the following format:
N K
x1 x2 … xN
输出
Print the minimum time required to light K candles.
样例输入
5 3 -30 -10 10 20 50
样例输出
40
提示
He should move and light candles as follows:
- Move from coordinate 0 to −10.
- Light the second candle from the left.
- Move from coordinate −10 to 10.
- Light the third candle from the left.
- Move from coordinate 10 to 20.
- Light the fourth candle from the left.
思路:
贪心.
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
#define inf 0x3f3f3f3f
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
ll n, k;
ll ans = inf;
std::cin >> n >> k;
std::vector<ll> a(n + 1);
for (int i = 1; i <= n; i++)
std::cin >> a[i];
for (int i = 1; i + k - 1 <= n; i++)
{
ll l = i, r = i + k - 1;
ans = std::min(ans, a[r] - a[l] + std::min(std::abs(a[l]), std::abs(a[r])));
/*我们可以从最大的数开始,逐渐取最小值,主要是这个过程不太好懂,r=i+k-1,因为正好
和l相隔k个点(加上他们自己),我们一组一组的找最小值,a[r]-a[l]是相隔的距离,abs就是找的绝对值,
代表最小的距离,就要先去哪一个点。如果实在不好理解,你可以把每个ans输出出来看一下,
应该就好理解了,*/
}
std::cout << ans;
return 0;
}问题 U: 野外长跑
题目描述
明明的学校为了宣传创文,特地组织了一次野外长跑活动。如下图所示,长跑的线路安排在一片连绵起伏的山坡上,工作人员预先在长跑路线的n个坡峰和坡谷处分别设置地点标记p1,p2,…,pn,并测量了每一个标记地点的海拔高度hi(0<hi≤100)以及相邻两个标记地点的路程si(0<si≤100)。假设每两个相邻标记地点之间的线路都近似一段弧线,并且与两地点之间的直线距离相差很少以至可以忽略其差别。好奇的明明想知道在这条长跑路线上,离起跑点最近的海拔最高点与最低点的直线距离是多少?
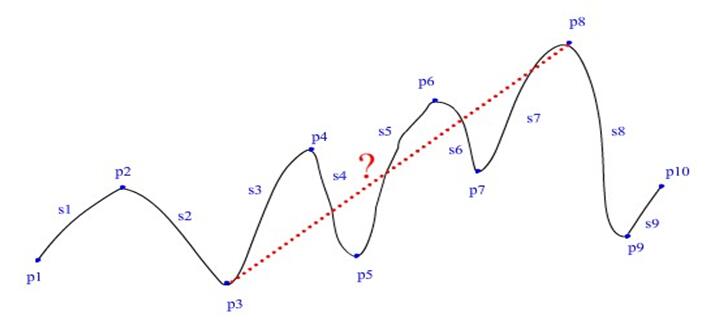
输入
第一行:一个整数n(2≤n≤100),表示有n个标记地点。
第二行:n个空格分开的整数hi,第i个整数代表第i个标记地点的海拔高度。
第三行:n-1个空格分开的整数si,第i个整数代表第i段路程。
输出
一个实数,表示长跑线路上海拔最低点与海拔最高点的直线距离。(最终结果四舍五入保留两位小数)。
样例输入
8 2 4 1 5 3 11 4 6 3 4 5 3 10 9 3
样例输出
15.04
提示

如上图所示,设三角形ABC为直角三角形,c为斜边,a,b分别为两条直角边,那么a,b,c三边有如下关系:
c2=a2+b2,a2= c2-b2 ,b2= c2-a2
如果要求
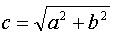
,则 (这称为“开平方”运算)
sqrt(x)为开平方函数,例如sqrt(9)的值为3, sqrt(6.25)的值为2.5 。
思路:
我们假设每一条线都是很值的情况下。
我们把最高点与最低点的直线叫做P。
要求这条直线的长度。直接求不是很好求。所以呢,我们需要用别的求法。相信大家都知道勾股定理吧。a²+b²=c²。我们可以利用这条关系来解决这道奇妙的问题。首先,我们知道了很多上坡路和下坡路和平路的距离这个距离我们把它看作三角形的斜边。我们来构造这样一个三角形。注意:这个三角形是一个直角三角形。再沿着斜边靠上一点的那一个点往下做一条高直到这条高的下面的那个点的高度等于较矮点的高度时停止。在下哦那个较矮点到高的较矮点链接一条线段。这样就组成了一个直角三角形。因为我们知道斜和一条直角边的长度,我们叫可以用勾股定理来求另一条直角边的长度(即底边)。在从最小高度到最大高度的两点之间,所有三角形底边的和就是一条直角边,两点的高度只差就是另一条直角边。在用一次勾股定理求出斜边即可。
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
double maxh = -1, minh = 101, h[101], s[100], b, w, a, x, winer, losser;
int n;
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n;
for (int i = 1; i <= n; i++)
{
std::cin >> h[i];
if (h[i] > maxh)
{
maxh = h[i];
winer = i;
}
if (h[i] < minh)
{
minh = h[i];
losser = i;
}
}
if (losser > winer)
{
int y = losser;
losser = winer;
winer = y;
}
for (int i = 1; i <= n - 1; ++i)
{
std::cin >> s[i];
}
for (int i = losser; i < winer; ++i)
{
w = std::sqrt(s[i] * s[i] - (h[i + 1] - h[i]) * (h[i + 1] - h[i]));
a = a + w;
}
x = std::sqrt((maxh - minh) * (maxh - minh) + a * a);
std::cout << std::fixed << std::setprecision(2) << x;
return 0;
}问题 V: 蜡烛
题目描述
奶牛bessie有n根蜡烛,第i根蜡烛的长度是h[i]. bessie最近刚上完小学,只会加减法。它想知道它的n根蜡烛最多能用多少个晚上。由于bessie比较胆小,因此它第一个晚上只点燃一根蜡烛,第二个晚上点燃两根蜡烛,第三个晚上点燃三根蜡烛…第i个晚上它必须要点燃i根蜡烛。每根被点燃的蜡烛,它燃烧一个晚上会使得它的长度减少1。一旦蜡烛的长度变成0,那么该根蜡烛就用完了。如果第i个晚上bessie发现不够i根蜡烛用了,那么bessie最多就只能用i-1个晚上.
Bessie想知道,它该如何选择每个晚上点燃哪些蜡烛,使得它的n根蜡烛能用尽量多的晚上。输出最多能用多少个晚上。
输入
第一行:一个整数n,其中1≤n≤50.
第二行:n个整数,第i个整数表示第i根蜡烛的长度h[i],1≤h[i]≤100.
输出
一个整数,总共最多能用多少个晚上。
样例输入
【样例1】 3 2 2 2 【样例2】 4 5 2 2 1
样例输出
【样例1】 3 【样例2】 3
思路:
贪心.
参考代码:
#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#define ll long long
bool cmp(int a, int b)
{
return a > b;
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, t, ans{};
std::cin >> n;
std::vector<int> h(n + 1);
for (int i = 1; i <= n; i++)
std::cin >> h[i];
std::sort(h.begin() + 1, h.end(), cmp);
for (int i = 1; i <= n; i++)
{
t = 0;
ans++;
for (int j = 1; j <= i; j++)
{
if (!h[j])
{
std::cout << ans - 1;
return 0;
}
h[j]--;
}
std::sort(h.begin() + 1, h.end(), cmp);
}
std::cout << ans;
return 0;
}

![[future 2022] 基于特征选择的DDoS攻击流分类方法](https://img-blog.csdnimg.cn/img_convert/7532f63af8e7985a520116bcfa825766.jpeg)