leetcode 困难 —— N 皇后（简单递归）

news2025/5/30 14:47:14

（不知道为啥总是给这种简单的递归设为困难题，虽然优化部分很不错，但是题目太好过了）

题目：
按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个不同的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

题解：
首先看眼数据范围，1 <= n <= 9，这么小的数据，估计就是枚举了

那我们怎么枚举呢，遍历在前 i 行已经确定的情况下，第 i + 1 行所有可取的情况
（第 0 行则每一列所有都可取）

那我们怎么判断可不可取呢
① 该列和以前行的列重合
② 该列和以前行的列在一条斜线上（当前行 - 以前行 = | 当前列 - 以前列 |）

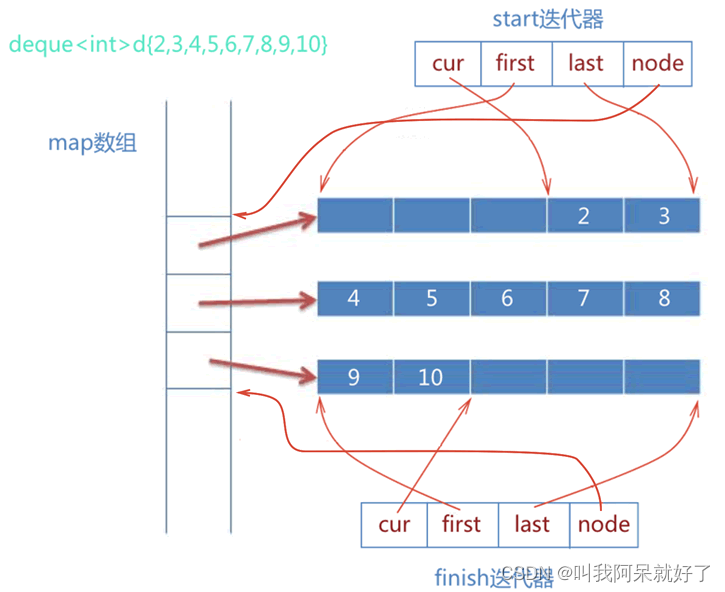
然后我们把以前的行的选择列，用一个字符串表示即可
例 “13524”，第一行选第一列，第二行选第三列…

代码如下：

class Solution {
public:
    vector<string> solve(string pre, int n) {
        vector<string> res;
        bool flag[10];
        for(int i = 0; i < n; i++) {
            flag[i] = true;
        }
        int m = pre.size();
        for(int i = 0; i < m; i++) {
            flag[pre[i] - '0'] = false;
            if(pre[i] - '0' - m + i >= 0) flag[pre[i] - '0' - m + i] = false;
            if(pre[i] - '0' + m - i < n) flag[pre[i] - '0' + m - i] = false;
        }
        vector<string> temp;
        for(int i = 0; i < n; i++) {
            if(flag[i] && m != n - 1) {
                temp = solve(pre + char(i + '0'), n);
                res.insert(res.end(), temp.begin(), temp.end());
            }
            else if(flag[i] && m == n - 1) {
                res.push_back(pre + char(i + '0'));
            }
        }
        return res;
    }
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string> > res;
        vector<string> t = solve("", n);
        for(int i = 0; i < t.size(); i++) {
            vector<string> temp;
            for(int j = 0; j < n; j++) {
                string str = "";
                for(int k = 0; k < n; k++) {
                    if(k != t[i][j] - '0') {
                        str = str + '.';
                    }
                    else {
                        str = str + 'Q';
                    }
                }
                temp.push_back(str);
            }
            res.push_back(temp);
        }
        return res;
    }
};

接下来，我们考虑优化

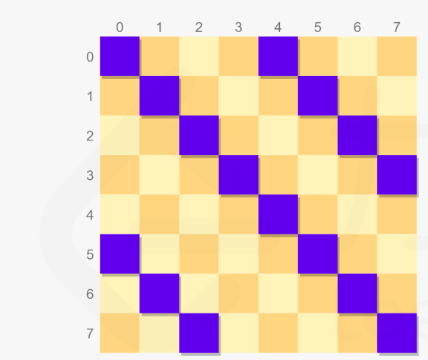
在这里插入图片描述