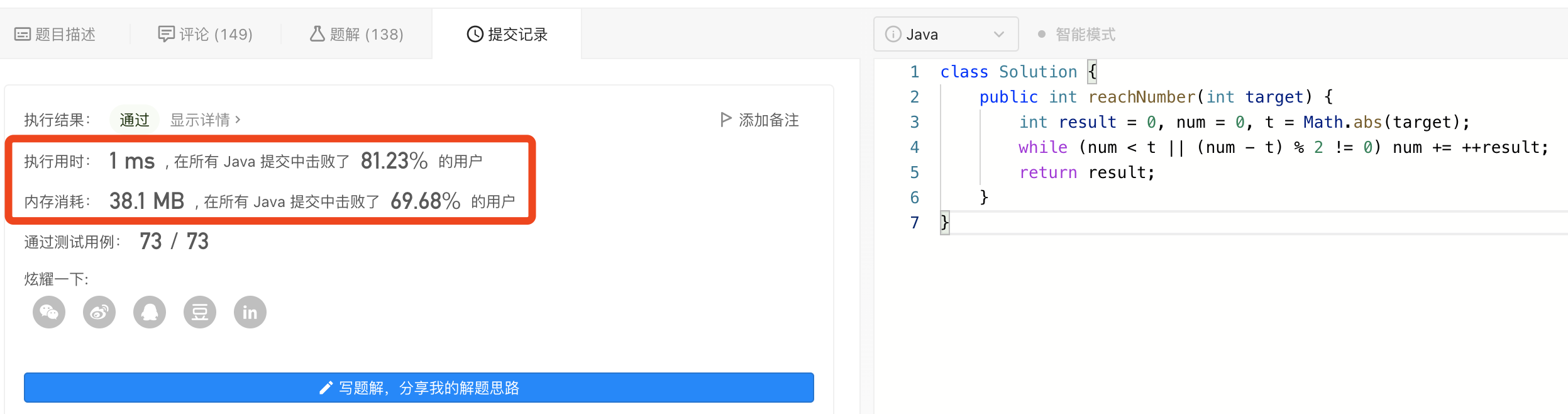
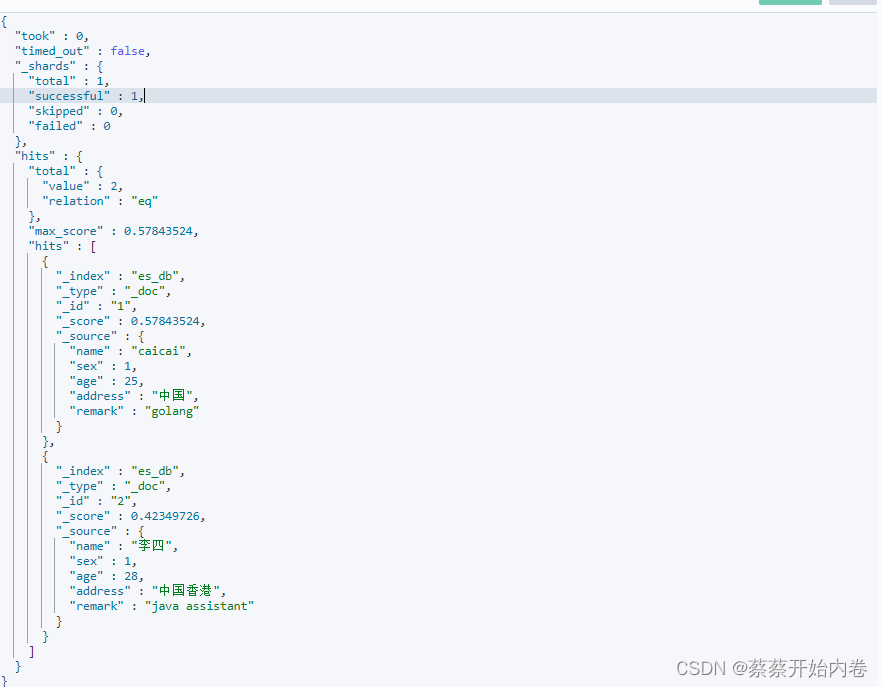
高级FPGA设计结构实现和优化_静态时序分析
- 标准分析
- 锁存器
- 组合反馈
标准分析
静态时序分析(STA)指的是在一个设计中与一组约束有关的所有时序路径的综合性分析,为了确定一个设计是否是“时序一致的”。由FPGA设计者遇到的基本路径是输入到触发器、触发器到触发器、触发器到输出,如下图所示:

这些路径与输入延时、输出延时、建立和保持时序要求等有关。建立时序分析指的是长路径分析,保持时序分析指的是短路径分析。最大频率由设计中最长路径也称为关键路径所确立。路径分析设计比逻辑延时更多的考虑,如下图所示:

最大路径延时是时钟到Q端延时、逻辑和布线延时、建立时间和时钟偏移的函数。最大频率(最小周期)将由数据通道延时之和减去时钟偏移确定,关于最小时钟周期的计算公式在我此专栏的高级FPGA设计结构实现和优化_(一)结构设计有讲到,最高速度或最大频率可以直接按照著名的最大频率方程定义(不管时钟到时钟的抖动):
T
m
a
x
=
1
T
c
l
k
−
q
+
T
l
o
g
i
c
+
T
r
o
u
t
i
n
g
+
T
s
e
t
u
p
−
T
s
k
e
w
T_{max} = \dfrac{1}{T_{clk-q}+T_{logic}+T_{routing}+T_{setup}-T_{skew}}
Tmax=Tclk−q+Tlogic+Trouting+Tsetup−Tskew1
其中
T
m
a
x
T_{max}
Tmax是时钟可允许的最大频率,
T
c
l
k
−
q
T_{clk-q}
Tclk−q是从时钟到达直至数据到达Q端的时间,
T
l
o
g
i
c
T_{logic}
Tlogic是逻辑通过触发器之间的传播延时,
T
r
o
u
t
i
n
g
T_{routing}
Trouting是触发器之间的布线延时,
T
s
e
t
u
p
T_{setup}
Tsetup是下一个时钟上升沿之间数据必须到达D端的最小时间(建立时间),
T
s
k
e
w
T_{skew}
Tskew是启动触发器和捕捉触发器之间时钟的传播延时。
如果要求的周期比
T
m
a
x
T_{max}
Tmax定义的最小周期大,则有正的滞后,如下图所示:

这张图里上面是数据Q和时钟Clock达到触发器的时间,下面是数据D被捕获的时间和时间偏移的时间,Skew指的是偏移的大小,Setup是数据在时钟沿有效之前的建立时间,如果说数据在捕获时钟减去建立时间之前到达触发器,就会出现正的Slack(滞后),相反,如果在这之后才到达触发器,那么此路径将有负的滞后,显然这不满足时序,因为建立时间不满足。
再看下一种情况,当数据在时钟上升沿之后太久才抵达一个触发器时,这时会容易发生保持冲突,添加一个附加的缓冲器相对容易修复。由于布线矩阵的内在延时在FPGA设计中保持延时冲突是罕见的。如果保持冲突发生。它通常表示一个时钟偏移问题。
除了定义系统时钟的准确约束,定义任何路径的约束也是重要的,它可以是不严格的。两个落入这个范畴的最通常的约束是多周期和假路径。多周期路径在下图中说明。

左边是典型路径,右边是多周期路径,多周期路径允许约束的信号在时序终点之间n个周期传播。注意到即使用一个多周期路径,建立和保持要求仍然有效。这是因为不管数据在哪个时钟沿到达,如果它到达太接近时钟沿,准稳态条件仍然可能发生。如果在立即跟随的时钟周期不需要利用数据,多周期路径可以作为一个约束来添加。当连接到不要求数据立即到达的器件时,这个情况可能发生。在DSP应用中有固定的采样率和每个采样可用的时钟数,这个情况常常发生。
假路径类似于多周期路径,在路径中不要求在单个时钟周期传播信号。差别是假路径逻辑上不可能用设计支配。换言之,尽管时序分析工具把物理路径看成从一个点通过一系列逻辑门到达另一点,在规范的操作期间一个信号在这两点之间传播逻辑上是不可能的。下图用来表示情况:

因为在设计的规范操作期间路径从不被切断,静态时序分析工具不管这些点之间的路径,在时序优化和关键路径分析期间不予考虑。带许多有效周期(大于n)的多周期路径与假路径之间的主要差别是,多周期路径仍然检验建立和保持的要求,并仍然被包含在时序分析中。对多周期路径静态失效时序是可能的,但是假路径将从不会有任何有关的时序冲突。
下面总结一下STA相较于基于仿真的动态时序分析的优点:
- 动态时序分析(用时序信息仿真)将只捕获少数问题。动态时序分析的用途知识对写仿真的人是好的。另一方面,
STA将在标准时序分析的边界内捕获所有的问题。换言之,STA对设计执行彻底的分析。对设计者唯一的要求是建立必要的条件和约束。 - 建立如抖动等特性的模型是很难的,因为这将产生十分复杂的测试台,把运行时间推导不合理的程度。
- 用
STA,各种条件的组合可以随运行时间正比地增加来校验。用动态时序分析,各种条件的组合以指数方式延长运行时间。 - STA不要求任何仿真周期,没有因事件调度而超载。
- STA提供更大范围的时序冲突,包括正的和负的建立和保持时间、最小和最大传输时间、时钟偏移、毛刺检测和总线竞争等。
- STA工具有自动地检测和识别关键路径、冲突行为和异步时钟的能力。
锁存器
当产生很高速的芯片,如微处理器,或者用其他高速流水线时,锁存器确实是有用的器件。锁存器只应该被专家型设计者利用,否则必须有好的理由才用它。大多数时间,锁存器由差的编码风格无意识地实现,然后出现在STA的报告中从而产生混乱。来看下面这个例子

可以看到输入和输出都是用的标准的D型上升沿触发器寄存,但是数据在触发器中间锁存。因为当控制信号iCtrl为高时,数据传递过去,但是对锁存器的控制为低时,输出被保持。从时序分析的观点,不考虑对锁存器的控制为高的条件,因为数据是简单地流过。类似地,不考虑控制为低的条件,因为输出被锁存,但是,要考虑的东西是数据实际上被锁存的时序,即从高到低的传输期间。
在某种意义上,对锁存器的控制类似在STA中一个时钟来对待,锁存器类似一个后沿触发器来对待。在下图中的波形说明时序一致的条件。

通常利用锁存器的拓扑被称之为双相锁存。在这个技术中,流水线的一级用是时钟的一个极性锁存,两边的各级用相反的极性锁存,如下图所示:

双相的模型可以仿照下面例子来进行设计。
module dualphase (
input iData,
input iCtrl,
input iNCtrl,
output oData
);
reg [3:0] wData;
assign oData = wData[3];
always @(*) begin
if(iCtrl) wData[0] <= iData;
if(iNCtrl) wData[1] <= wData[0];
if(iCtrl) wData[2] <= wData[1];
if(iNCtrl) wData[3] <= wData[2];
end
endmodule
在微处理器等的密集流水线设计中,双相锁存器可以提供较小的实现(锁存器比触发器更小)和低功率的实现(利用时钟的两个时钟沿来处理数据),注意:这个没必要扩展到所有的信号,如果一个电路没有很好定义的流水线(不总是可以定义好的),双相锁存器将是十分困难的。
组合反馈
组合反馈是通过逻辑的路径,从一条网线或一个导线开始,穿过组合逻辑门(与门、或门、多路选择等),在相同的网线结束,没有通过任何同步元件。一般,组合反馈环路是设计错误的结果,应该由综合工具标记为一个警告。这些也引起仿真器的问题(特别是没有组合延迟时)。
取决于设计的技术条件,组合反馈环路将或者呈现出振荡行为(由反相器和延时元件构建的自由运行振荡器),或者包含存储元件的特性(基本的锁存器和触发器可以用交叉耦合的与非门构建)。虽然用组合反馈构造有限数量的有用电路是可能的,但是一般没有方便的方式执行时序分析,因为终点不是时序元件。代替测量从一个触发器到另一个时序,设计者需要人工地在约束中定义时序的终点。这里有一个自由运行振荡器的例子:
//BAD CODINIG STYLE
module freeosc (
input iOscEn,
input iOutEn,
output oDat
);
wire wdat;
assign wdat = iOscEn ? !wdat : 0;
assign oDat = iOutEn ? wdat : 0;
endmodule
表示的是如下电路图:

除非工具明显地阻止综合组合环路,否则将综合这个设计。在分析期间,STA将只包含从输入到输出的路径。事实上。STA工具大概没有必需的数据来测量环路本身的延时。为了解决这个问题,必须添加一个时序终点到至少一条网线。在这种情况下,可以添加一条网线wdat(是反馈的网线)。在Xilinx实现中,用户约束文件(.ucf)的约束将是:
NET "wdat" TPSYNC = "looptime";
TIMESPEC "ts_looptime" = FROM "looptime" TO "looptime"
1 ns;
在上面的约束中,放置一个时序终点到网线wdat作为时序分组looptime的一部分。然后放置一个约束到looptime,使得STA有一些东西进行测量。STA现在将报告约850ps作为环路延时。


![[CSS]常见布局技巧](https://img-blog.csdnimg.cn/a1d36e1f71704f06af7586907ea070a2.png)