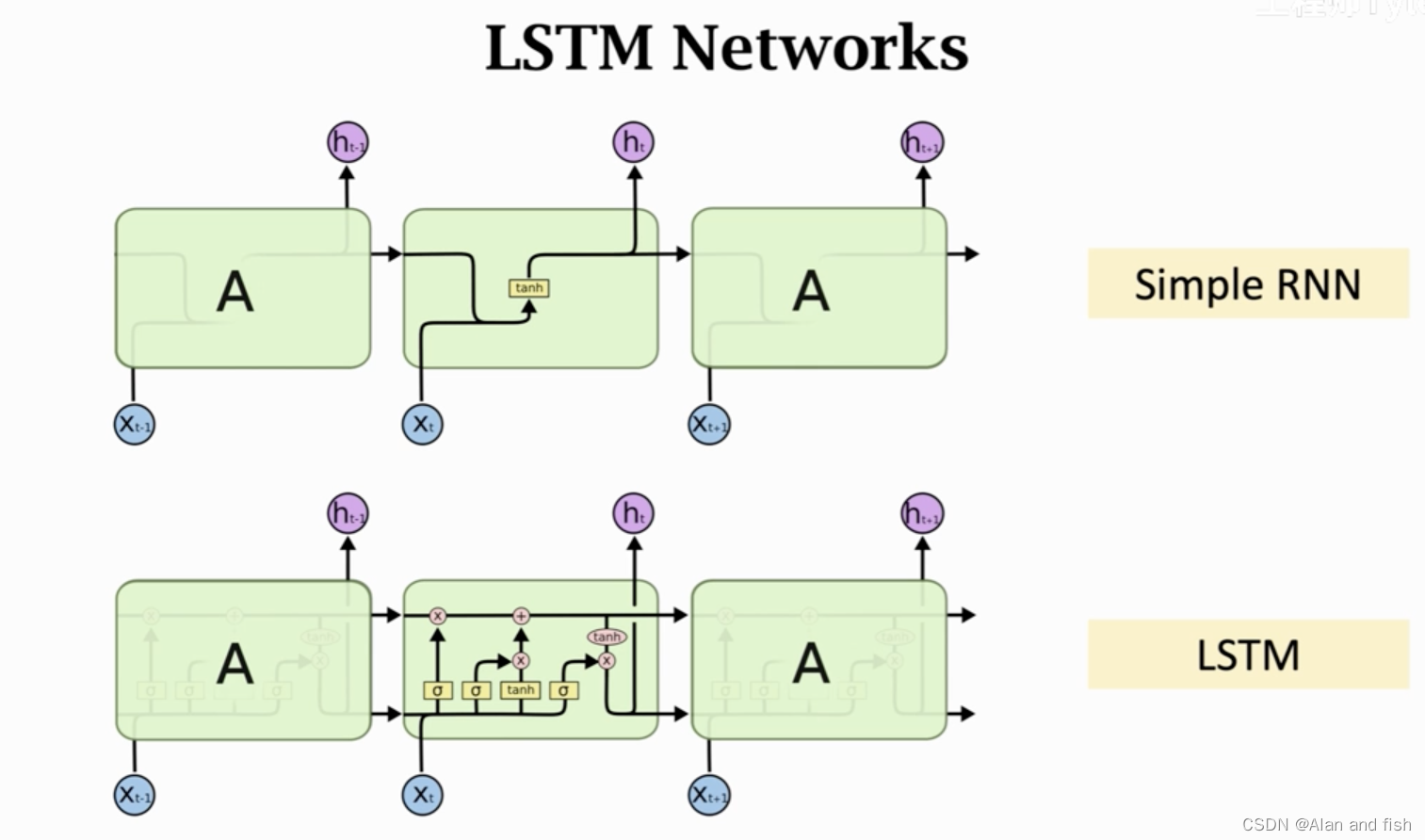
lstm类似于Simple_RNN,但是又比他复杂很多.我是参考这个视频的老师讲解的,这个老师讲解的非常好.https://www.bilibili.com/video/BV1FP4y1Z7Fj?p=4&vd_source=0a7fa919fba05ffcb79b57040ef74756
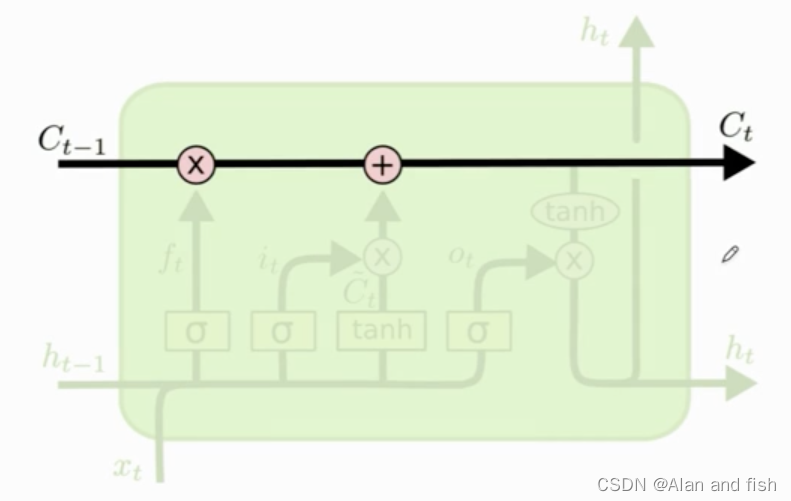
lstm的最重要的设计就是那一条传输带,即为向量
C
t
C_t
Ct,过去的信息通过他传送给下一个时刻,就是依靠传送带避免梯度消失.
遗忘门(forget Gate)
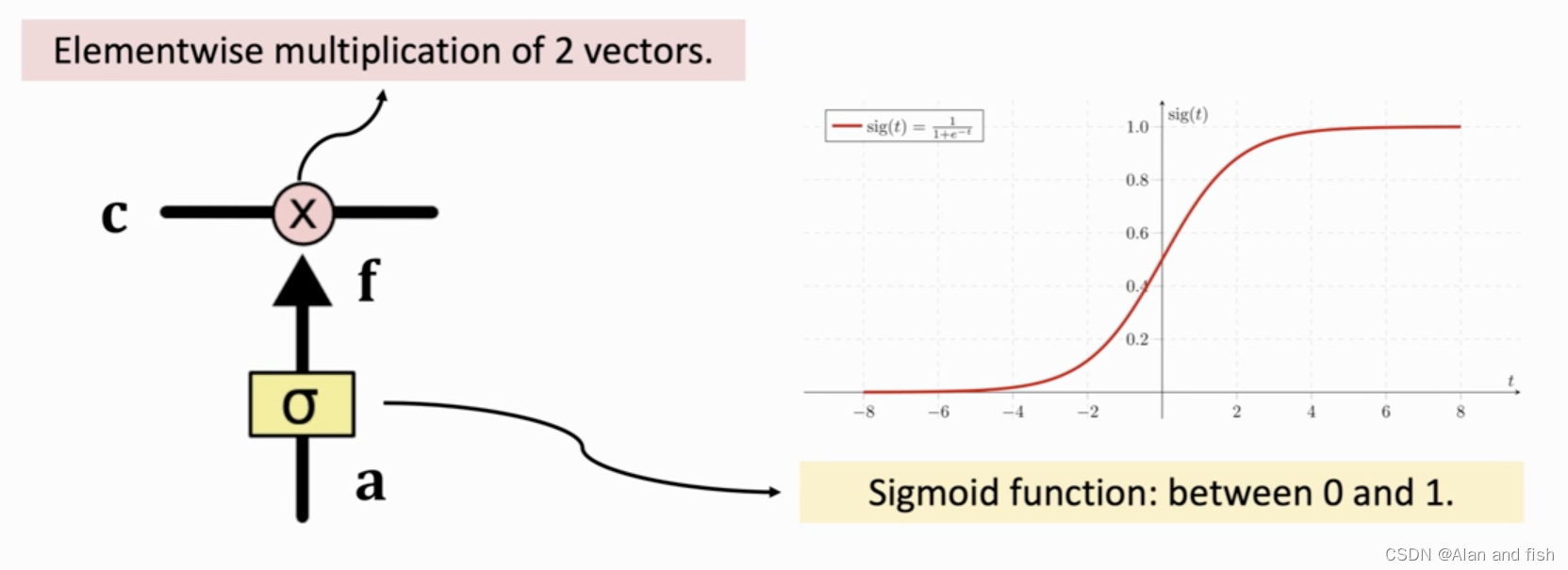
输入的是一个向量a,然后将a通过一个sigmoid函数,sigmoid函数将其归一化到0~1之间.比如下面这个矩阵,将其中的每个数字都归一化到了0-1之间,在归一化之后维度不发生改变.
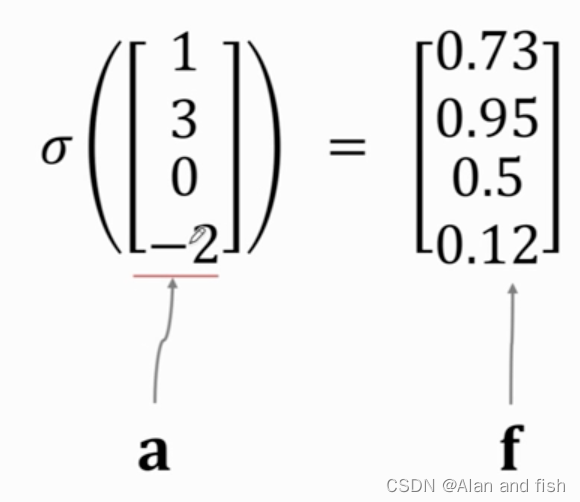
然后将归一化的向量f与签一个输出的向量c做内积,只需要把Elementwise multiplication的中与f向量中相同维度的值相乘即可,例如将0.9*0.5=0.45,得到输出output.
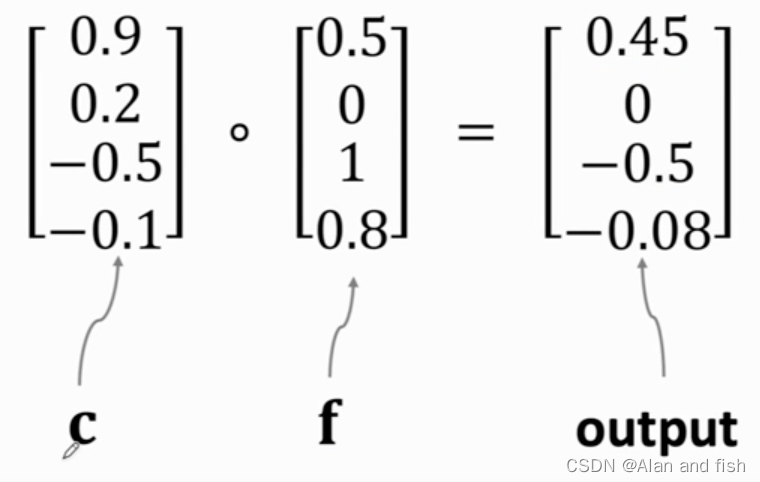
遗忘门可以让c有选择的通过,如果f对应维度的值为0,则这个维度的c就不能通过.如果f中对应维度的值为1,则c这个维度的数据就可以全部通过,就是他本身.
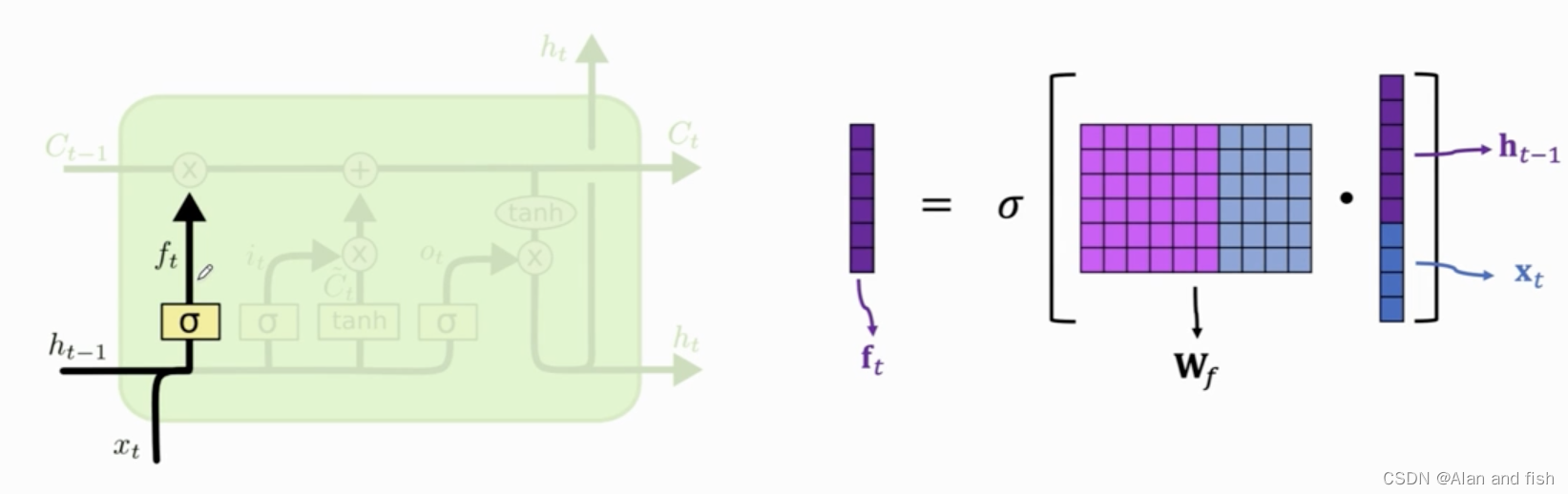
其中 f t f_t ft是上一个状态的输入 h t − 1 h_{t-1} ht−1与当前的输出 x t x_t xt做contact,然后乘以一个权重向量 W f W_f Wf,最后再做sigmoid得到向量 f t f_t ft,其中 f t f_t ft的每一个值都是介于0~1之间,权重参数 W f W_f Wf需要反向传播,学习得到.
输入门
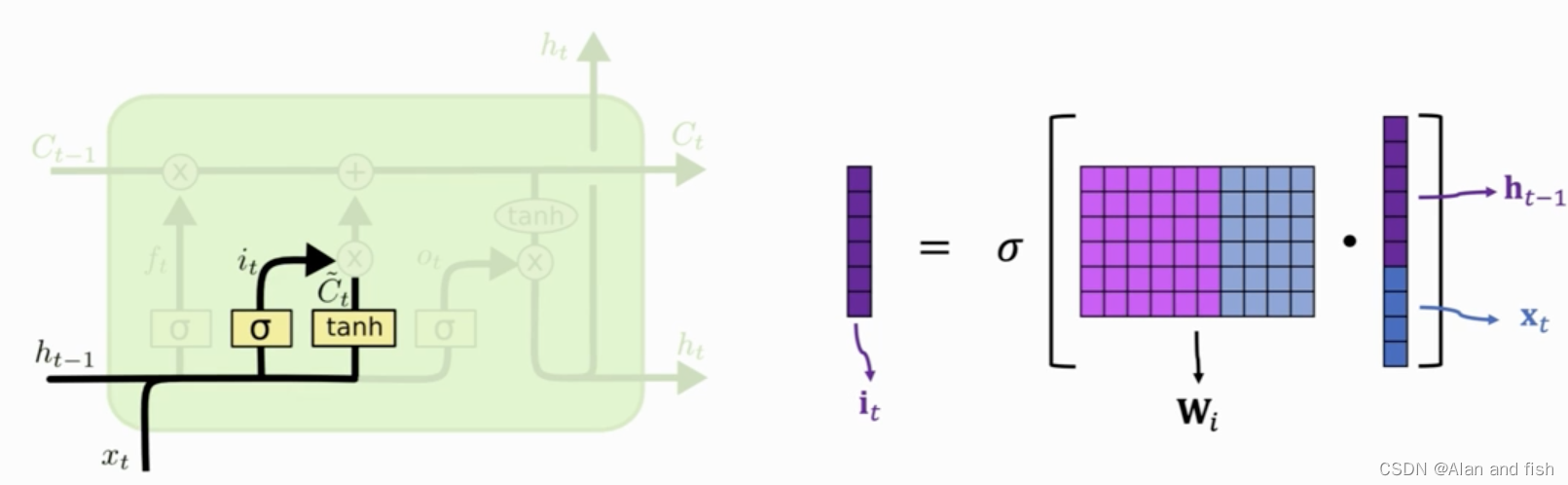
输入门的 i t i_t it依赖于旧的状态的 h t − 1 h_{t-1} ht−1和新的输入 x t x_t xt,很类似于遗忘门的计算过程,首先将 h t − 1 h_{t-1} ht−1与 x t x_t xt做contact,得到更高维的向量,然后与参数矩阵 W t W_t Wt做乘积计算,得到的结果通过一个sgmoid函数得到一个矩阵 i t i_t it,其中 i t i_t it中的每一个元素都是介于0~1之间,其中 W t W_t Wt是通过学习获得的.
更新输入信息(new value)
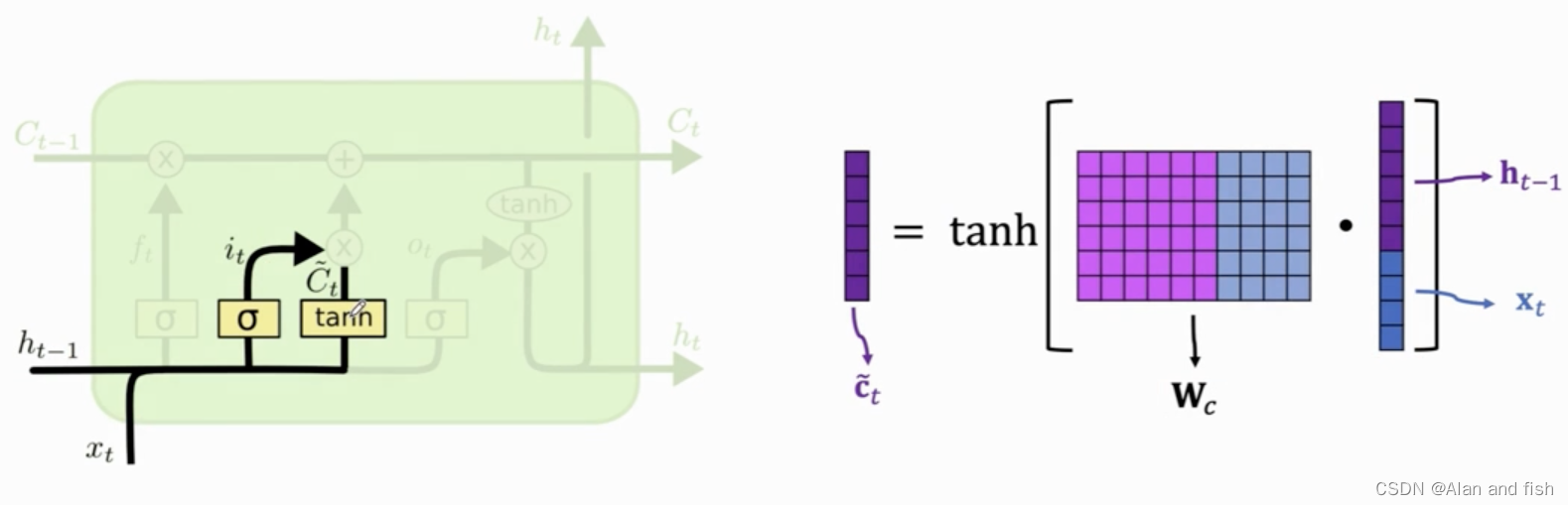
还需要计算一个值new value C ~ t \widetilde{C}_t C t,还是跟之前一样先将 h t − 1 h_{t-1} ht−1与 x t x_t xt做contact,然后乘以一个权重矩阵 W c W_c Wc,这时候使用的激活函数就与之间不同了,使用的是双曲正切函数,得到值是介于-1~1之间,其中 W c W_c Wc是通过学习获得的.
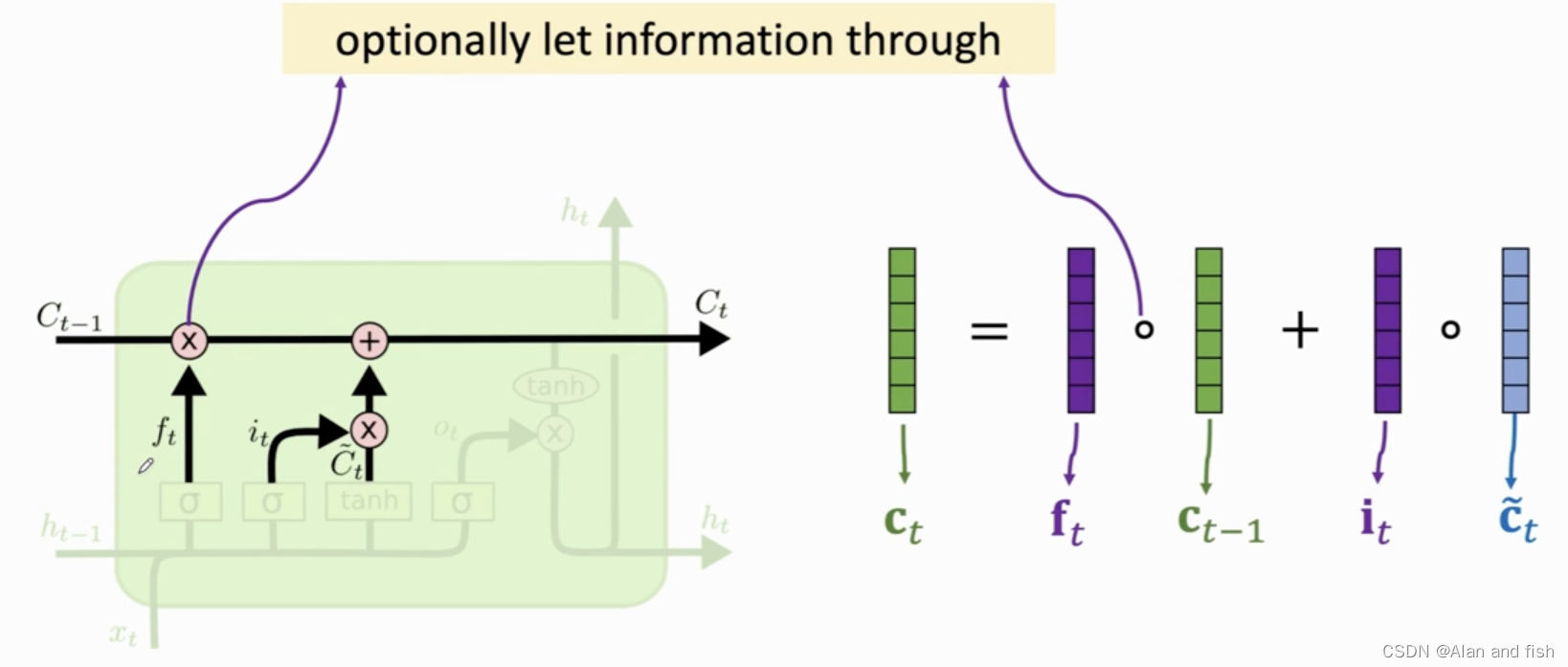
得到了 f t f_t ft, i t i_t it, C ~ t \widetilde{C}_t C t,然后将 f t f_t ft与上一个输入 C t − 1 C_{t-1} Ct−1里面的每一个元素做内积,如果 f t f_t ft中有的信息为0 ,则是对传送带上一个信息的选择性的遗忘,然后再将 i t i_t it, C ~ t \widetilde{C}_t C t做内积,得到新的输入信息,因为他们的维度都是相同的,则将他们全部加到一起,最后输出的信息 C t C_t Ct将作为下一个信息的输入.
输出层
更新完信息
C
t
C_t
Ct之后,就要计算输出信息,也就是状态向量
h
t
h_t
ht,计算过程如下:
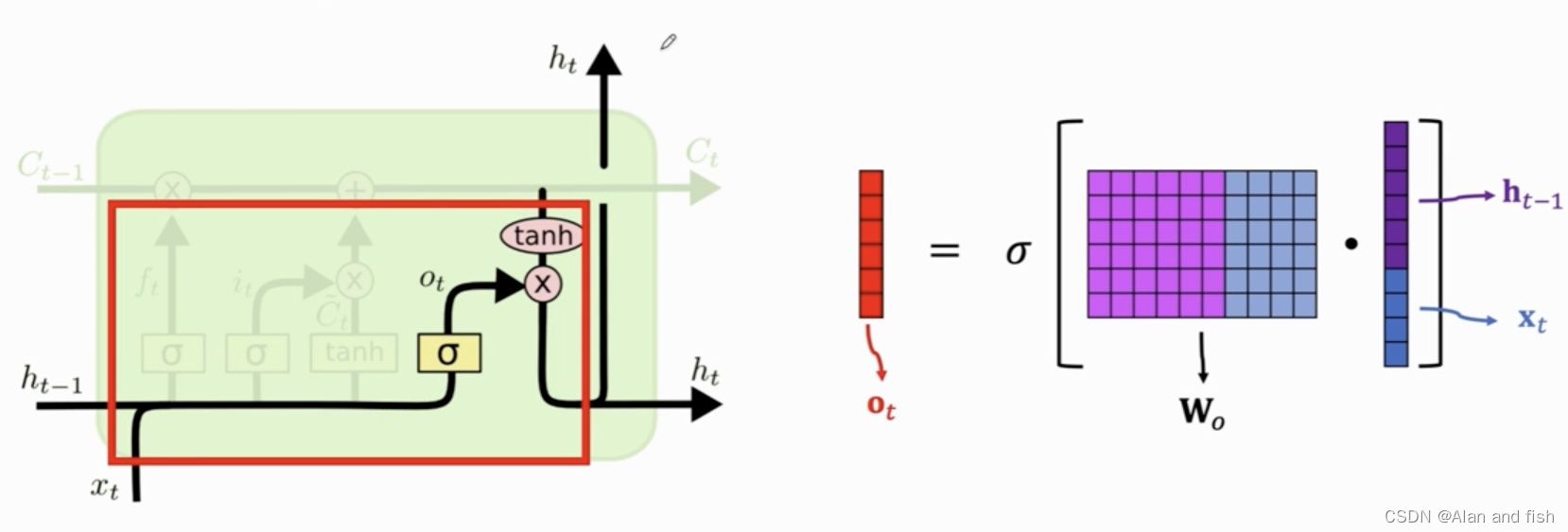
首先是计算输出门
O
t
O_t
Ot,计算过程是这样的,先将
h
t
−
1
h_{t-1}
ht−1与
x
t
x_t
xt做contact,然后乘以一个权重矩阵
w
o
w_o
wo,在将结果做sigmoid,得到
O
t
O_t
Ot,其中每一个元素都是介于0~1之间.
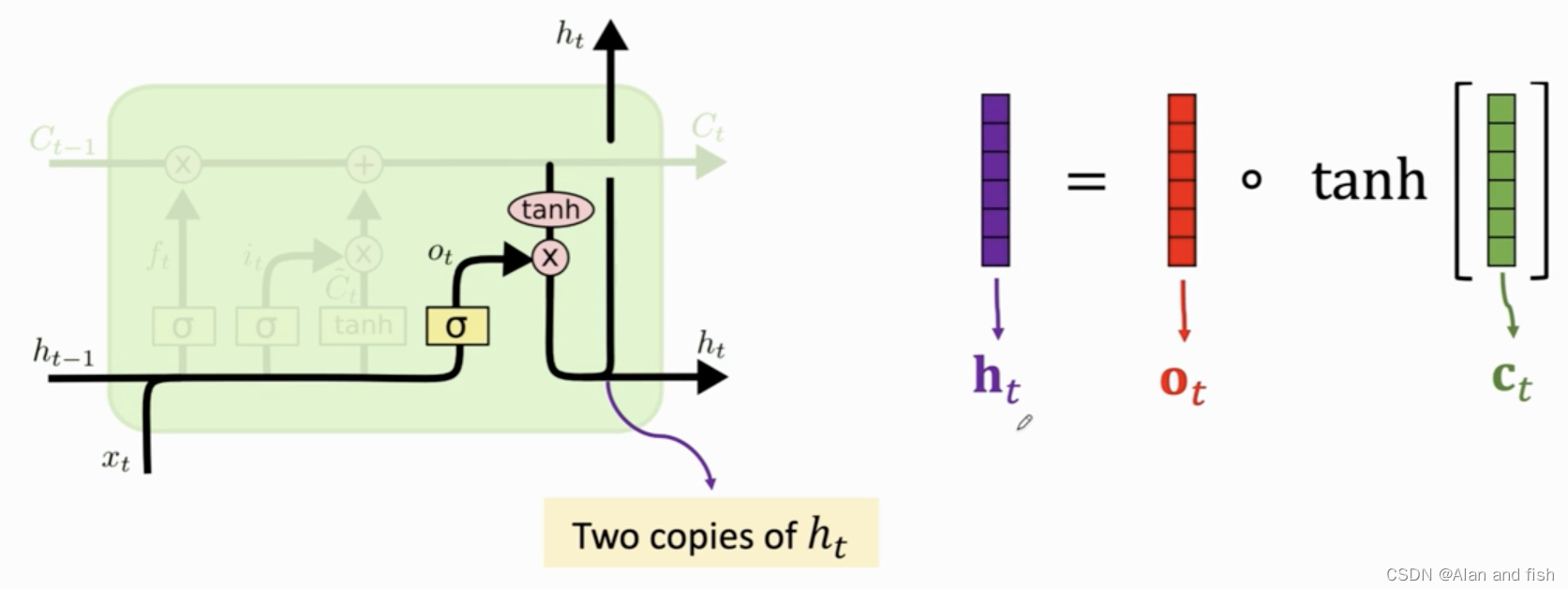
对传送带的每一个 c t c_t ct都进行双曲正切tanth,将值压缩到-1~1之间,然后与输出门 o t o_t ot做内积得到新的状态向量 h t h_t ht. h t h_t ht有两份copy,其中一份成为下一个lstm的输入,另外一个作为lstm的输出信息.对于当前状态,可以说一共有t个状态输入,所有的信息都积累在状态 h t h_t ht里面.
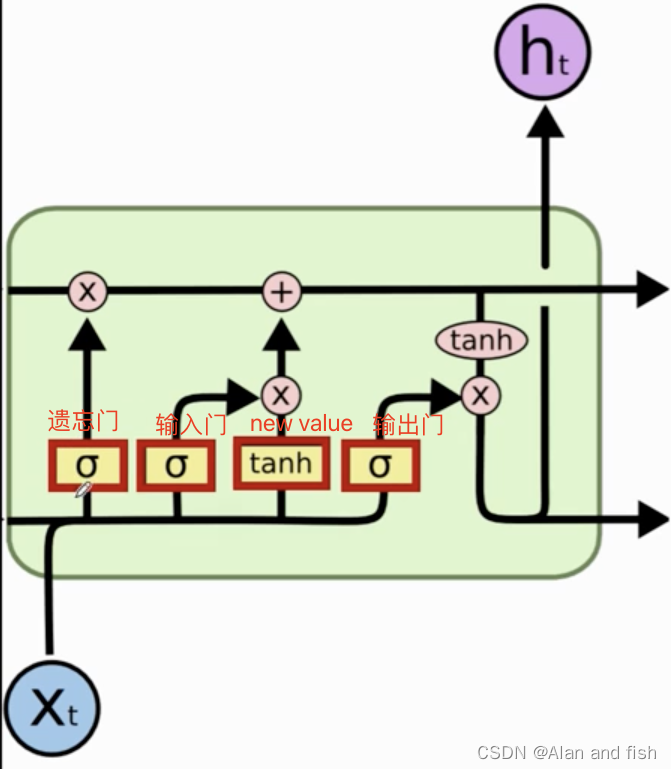
lstm一共有四个门,遗忘门,输入门,new value,输出门,则对应的是四个权重参数矩阵w,其中每个权重参数的维度为:
- 行:shape(h)
- 列:shape(h)+shape(x)
所以lstm的维度是:
4 ∗ s h a p e ( h ) ∗ [ s h a p e ( h ) + s h a p e ( x ) ] 4*shape(h)*[shape(h)+shape(x)] 4∗shape(h)∗[shape(h)+shape(x)]
LSTM的应用
- 情感分析
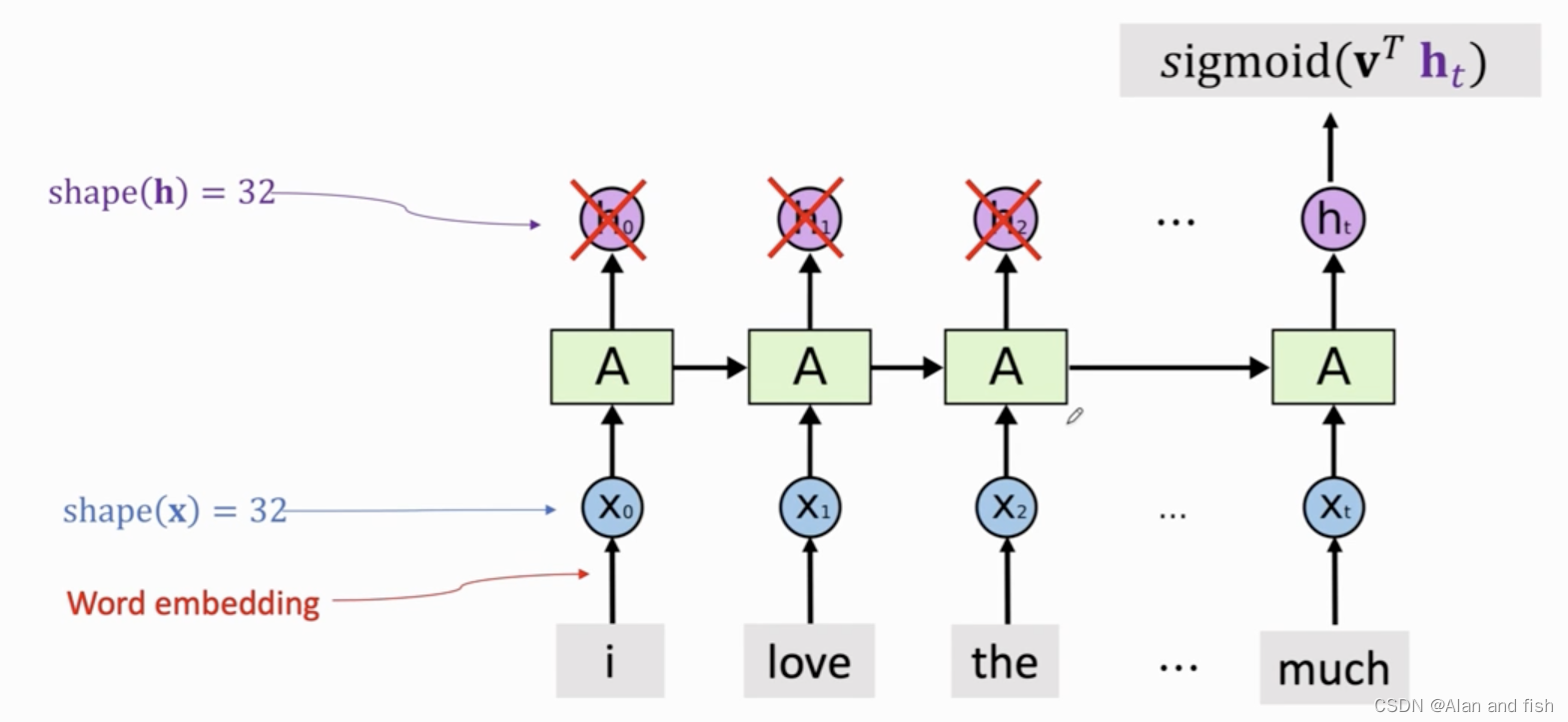
只需要将lstm的最后一个信息输出即可,然后放到sigmoid函数当中,最后得到了一个0-1之间的结果,代表正例和负例.






![2022/11/21[指针] 多维数组与指针的联系](https://img-blog.csdnimg.cn/f930824f9efa442ebc228e448f149dd8.png)