禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者!
文章目录
-
- 介绍
- 加载R包
- 数据下载
- 导入数据
- 数据预处理
- 相关性计算
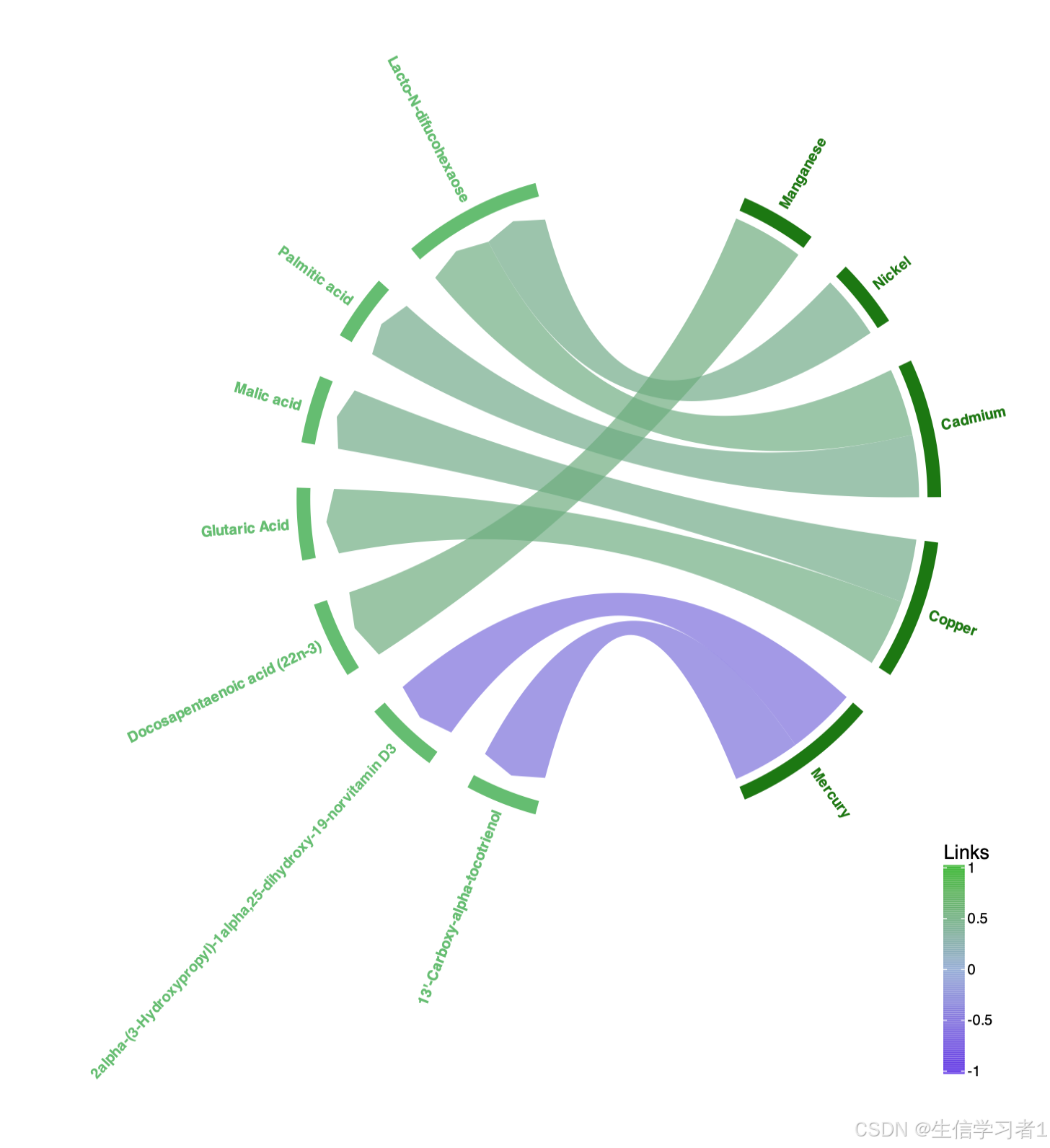
- 和弦图
- 系统信息
介绍
本文介绍了一个基于R语言的数据分析和可视化流程,主要用于生成和弦图(Chord Diagram)。和弦图是一种用于展示多个实体之间相互关系的可视化工具,广泛应用于生物信息学、生态学等领域。通过和弦图,可以清晰地展示不同数据集之间的相关性。
数据处理与分析
-
数据导入:首先,从本地文件导入两个数据集,分别是代谢物数据(
Metabolites.txt)和环境元素数据(Elements.txt)。这些数据通过read.delim函数读取,并进行初步筛选,去除总和为零的行。 -
相关性计算:将数据转置后,使用
corr.test函数计算相关性,采用Spearman方法,并对p值进行F