基于有效集MPC控制算法的直线同步电机simulink建模与仿真,MPC使用S函数实现

news2025/6/7 10:25:00

1.课题概述

2.系统仿真结果

3.核心程序

4.系统仿真参数

5.系统原理简介

6.参考文献

7.完整工程文件

1.课题概述

有效集算法通过迭代地选择一组 "有效" 约束，将约束优化问题转化为一系列无约束或等式约束优化问题。直线同步电机 (Linear Synchronous Motor, LSM) 是将电能直接转换为直线运动机械能的装置，其结构可视为旋转电机的 "展开" 形式。

2.系统仿真结果

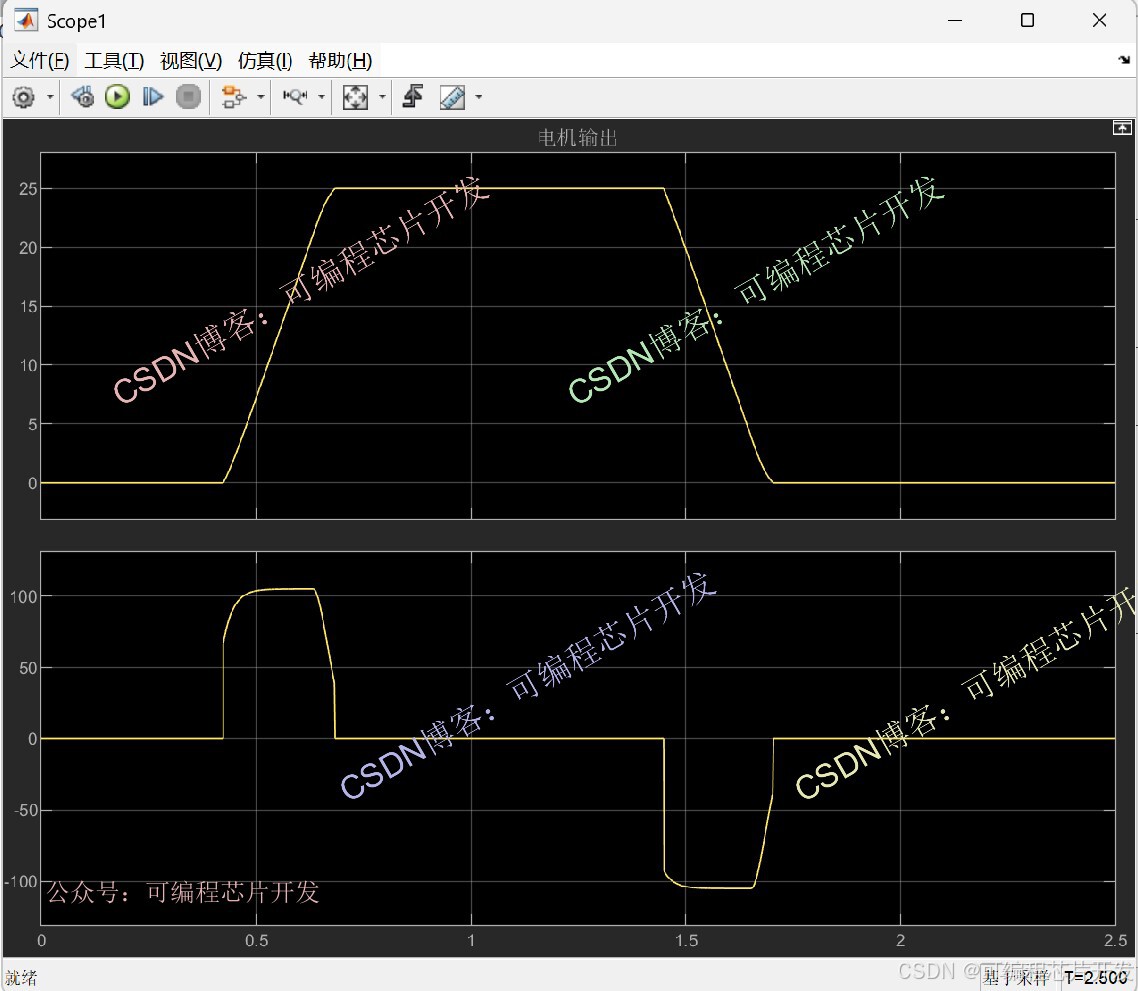
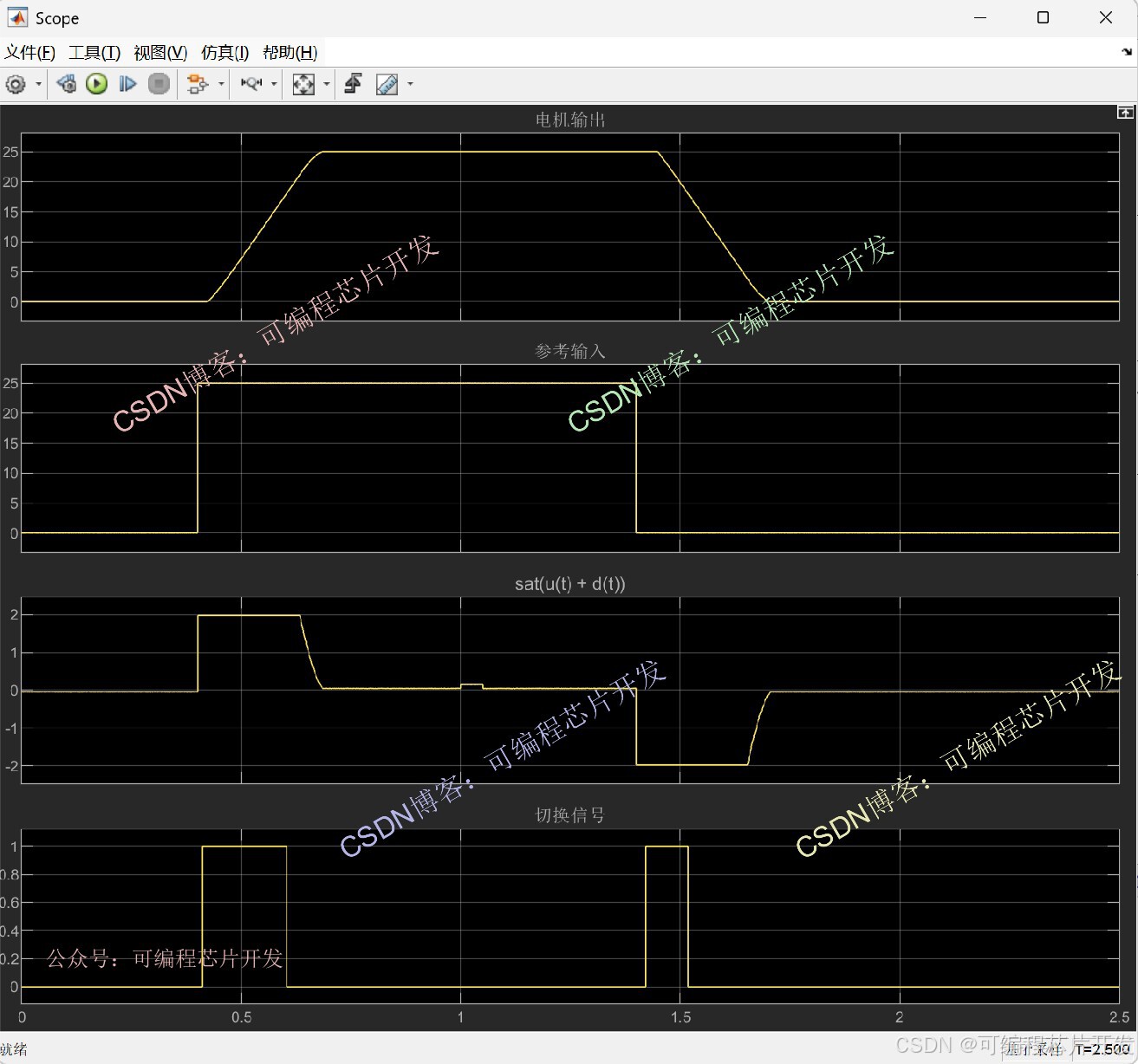
3.核心程序

matlab2024b

022_010m

4.系统仿真参数

%控制目标值
Position = 25;

%Sample time
T       = 0.001;   
Ts      = T;    
%直线电机空间状态方程参数
A = [-44.12,0;
          1,0]
B = [4;
     0]
C = [0,2.325]
D = [0]

umax = 20;

5.系统原理简介

模型预测控制 (Model Predictive Control, MPC) 是一种基于模型的优化控制策略，其核心思想是：

1.利用系统模型预测未来时刻的输出

2.求解有限时域内的优化问题，得到控制序列

3.只应用第一个控制动作，下一时刻重复上述过程 (滚动优化)

有效集算法通过迭代地选择一组 "有效" 约束，将约束优化问题转化为一系列无约束或等式约束优化问题。基本步骤如下：

1.初始化有效集A0

2.求解当前有效集下的子问题

3.检查所有约束的可行性

4.更新有效集，添加或删除约束

5.重复 2-4 直到收敛

对于二次规划问题，在第k次迭代：

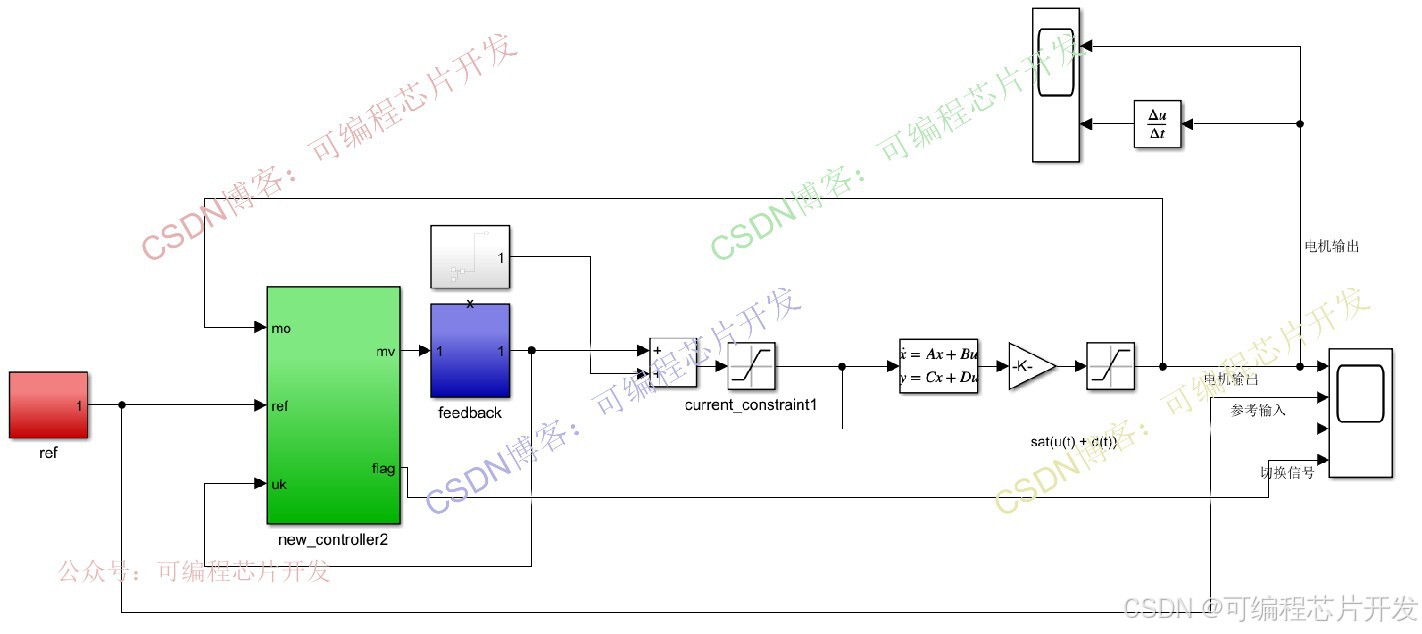
使用S函数设计有效集MPC控制器：

控制律设计

F_ = A/B'; F = F_'; I = eye(size(F,1));
fr = inv(C2*inv(I-A-B*F)*B(1));
fd = -fr*(C2*inv(I-A-B*F)*E(1));
UL = mean2(Fx*xk_ + fd*dk_ + fr*r);

稳定性分析与不变集计算

Gr = inv(I-A-B*F)*B(1)*fr;
Gd = inv(I-A-B*F)*(B(1)*fd+E);
lr = fr + F*Gr; ld = fd + F*Gd;
W = ww'*ww; % 正定矩阵
P = inv((A+B*F)'*(A+B*F))*W; % 求解Lyapunov方程
Cd = (1-delt)*umax/mean2(F*inv(P)*F');
chk = mean2(x_'*P*x_); % 状态误差二次型

有效集MPC优化求解：

Q = 0.5; lemd = 0.2;
N = length(x_);
JK = sum(x_'*Q*x_ + lemd*u_^2) + x_(N)'*P*x_(N);
% 搜索最小值对应的控制量
while(JKs>JK)
    JKs = sum(x_'*Q*x_ + lemd*uu_^2) + x_(N)'*P*x_(N);
    uu_ = 0.051*uu_;
end
UM = uu_(1) + sum(sum(us_k));