梯度下降算法原理及其在机器学习中的实践应用
引言
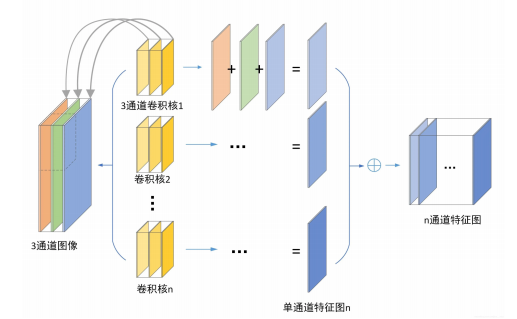
在机器学习领域,优化算法扮演着核心角色。其中梯度下降法作为最基础的优化方法,为神经网络、支持向量机等模型提供了参数优化解决方案。本文将深入解析梯度下降的数学原理,探讨其多种变体实现,并通过Python代码演示具体应用。
一、梯度下降基本原理
1.1 算法核心思想
梯度下降法通过迭代方式寻找目标函数的极小值点。其核心公式可表示为:
θ t + 1 = θ t − α ∇ J ( θ t ) \theta_{t+1} = \theta_t - \alpha \nabla J(\theta_t) θt+1=θt−α∇J(θt)
其中 α \alpha α表示学习率, ∇ J ( θ ) \nabla J(\theta) ∇J(θ)为目标函数的梯度。算法通过不断沿负梯度方向调整参数,逐步逼近函数最小值。
1.2 数学基础
考虑二次可微函数 J ( θ ) J(\theta) J(θ),在点 θ t \theta_t θt处进行泰勒展开:
J ( θ t + 1 ) ≈ J ( θ t ) + ∇ J ( θ t ) T ( θ t + 1 − θ t ) + 1 2 ( θ t + 1 − θ t ) T H ( θ t ) ( θ t + 1 − θ t ) J(\theta_{t+1}) \approx J(\theta_t) + \nabla J(\theta_t)^T(\theta_{t+1} - \theta_t) + \frac{1}{2}(\theta_{t+1}-\theta_t)^T H(\theta_t)(\theta_{t+1}-\theta_t) J(θt+1)≈J(θt)+∇J(θt)T(θt+1−θt)+21(θt+1−θt)TH(θt)(θt+1−θt)
当步长满足 α < 2 λ m a x \alpha < \frac{2}{\lambda_{max}} α<λ