目录
引言
1.冒泡排序
思路
代码实现
2.选择排序
思路
代码实现(存在易错点)
3.插入排序
思路
代码实现
4.希尔排序
思路
代码实现
5.堆排序
思路
代码实现
6.快速排序(快排)
一.三路划分
思路
代码实现
二.自省排序
思路
代码实现
7.归并排序
1.递归法
思路
代码实现
2.非递归法
思路
代码实现
8. 计数排序
思路
代码实现
总结(附排序训练OJ题)
引言
在计算机科学中,排序算法是非常基础且重要的内容。它可以将一组无序的数据按照特定的顺序(如升序或降序)进行排列。本文将详细介绍八大排序算法:冒泡排序、插入排序、选择排序、堆排序、希尔排序、快速排序、归并排序和计数排序,并结合代码进行分析。(本文展示代码均为升序)

先放一个前置的Swap交换函数方便函数调用:
//交换
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}1.冒泡排序
思路
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。每一趟交换的结果是把最大一个数放在最后。(以升序为例)走访数列的工作是重复地进行直到没有再需要交换,也就是说该数组已经排序完成。
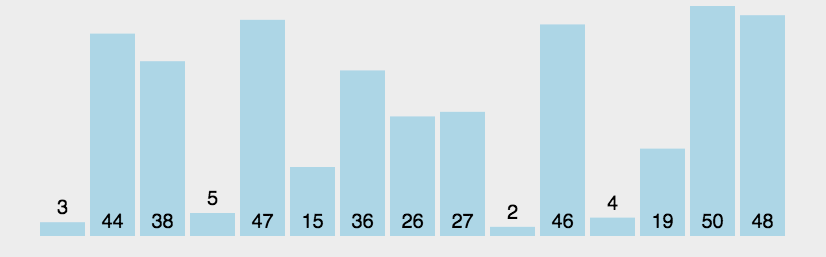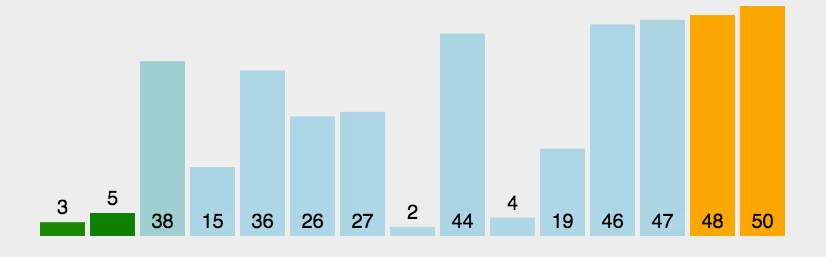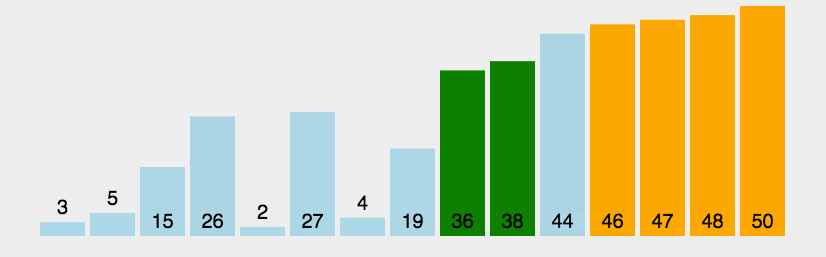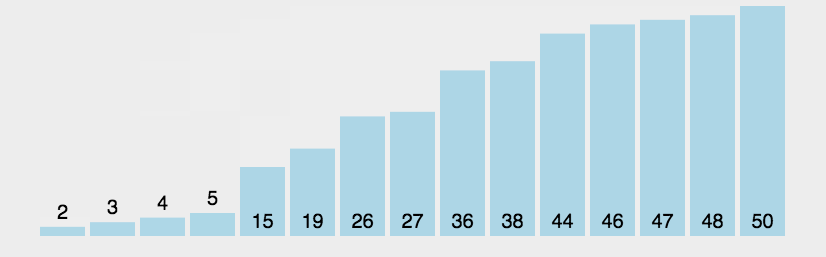
可定义一个flag变量,若第n(n>=0)次没有交换元素,则停止交换 。
时间复杂度:最好情况为 (O(N)),最坏情况为 (O(N^2))。
空间复杂度:(O(1))。
稳定性:稳定。
代码实现
//冒泡排序
void BubbleSort(int* a, int n)
{
for(int i = 0; i < n; i++)
{
int flag = 0;
for(int j = 0; j < n - i; j++)
{
if(a[j+1] > a[j])
{
Swap(&a[j+1], &a[j]);
flag = 1;
}
}
if(flag == 0)
{
break;
}
}
}2.选择排序
思路
选择排序是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
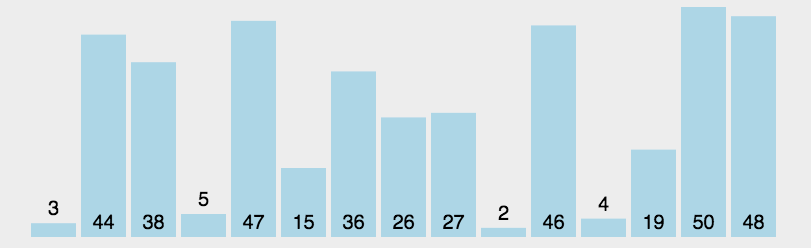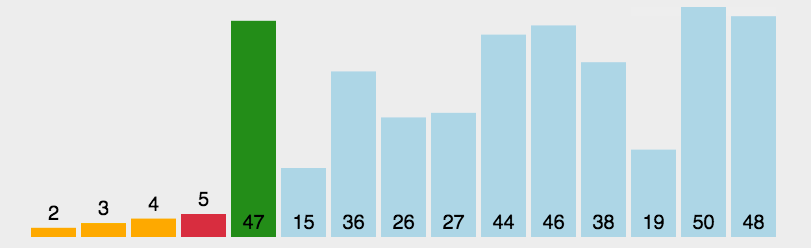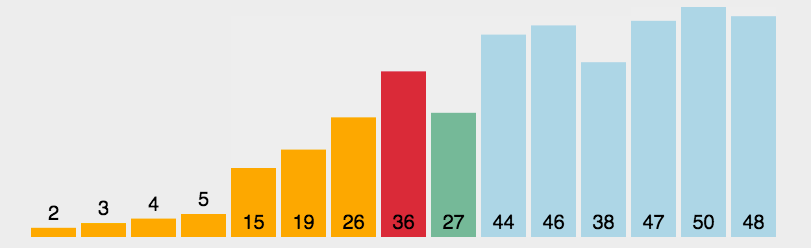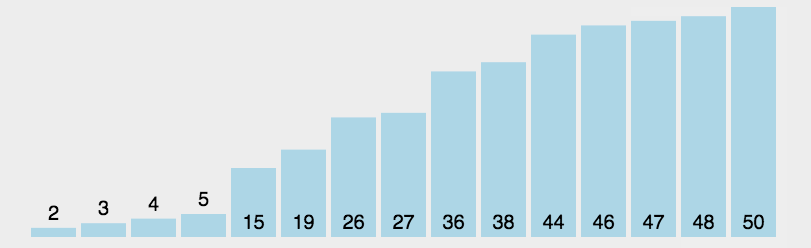
但是实际操作的时候,每次排一个显得尤为繁琐,因此我们可以一趟选出最大值与最小值,以此将其放在开头与结尾,这样可以让效率得到大大提升。
时间复杂度:(O(N^2))。
空间复杂度:(O(1))。
稳定性:不稳定。(易错)
代码实现(存在易错点)
//选择排序
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while(begin < end)
{
int min = begin, max = begin;
for(int i = begin + 1; i <= end; i++)
{
if(a[i] < a[min])
{
min = i;
}
if(a[i] > a[max])
{
max = i;
}
}
Swap(&a[begin], &a[min]);
if(begin == max)
max = min;
Swap(&a[end], &a[max]);
++begin;
--end;
}
}这里需要注意!如果max值出现在begin处,begin与min交换后需要把max 与min 的位置交换回来,以避免代码出现置换出错的问题。
3.插入排序
思路
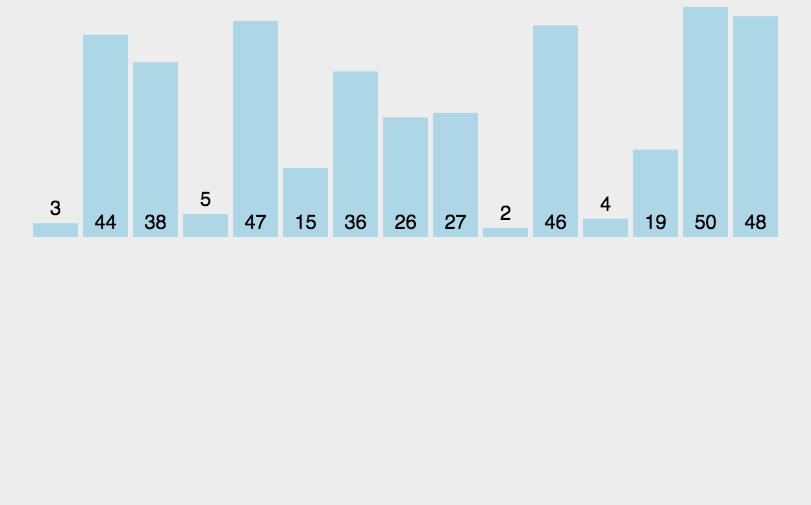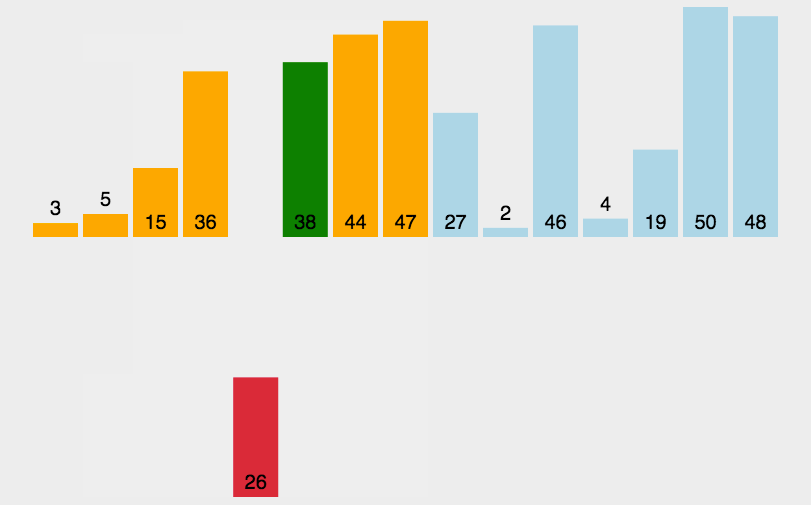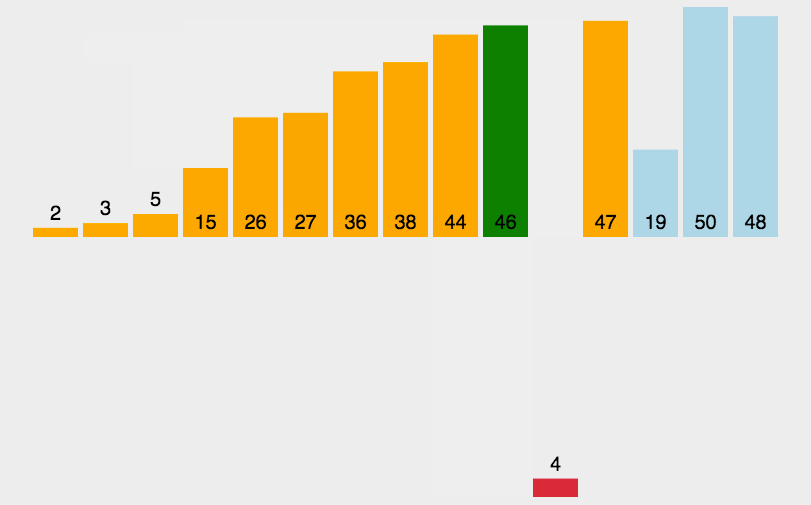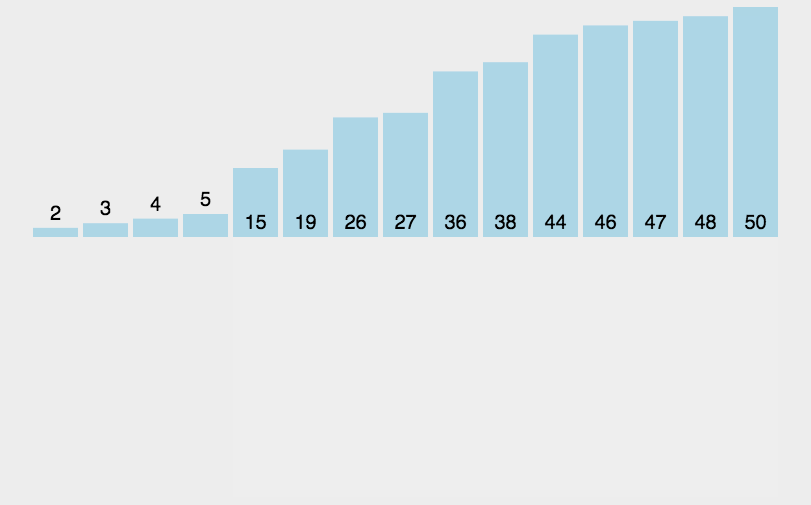
插入排序是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
时间复杂度:最好情况为 (O(N)),最坏情况为 (O(N^2))。
空间复杂度:(O(1))。
稳定性:稳定。
代码实现
//插入排序 最好O(N) 最坏O(N ^ 2)
void InsertSort(int* a, int n)
{
for(int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = a[end + 1];
while(end >= 0)
{
if(tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}4.希尔排序
思路
先给定一个小于n的整数gap,将所有距离为gap的元素分为一组,对每一组进行插入排序,再取比gap小的一个整数,重复上述操作,直到该整数取为1,即为插入排序,排序完成。
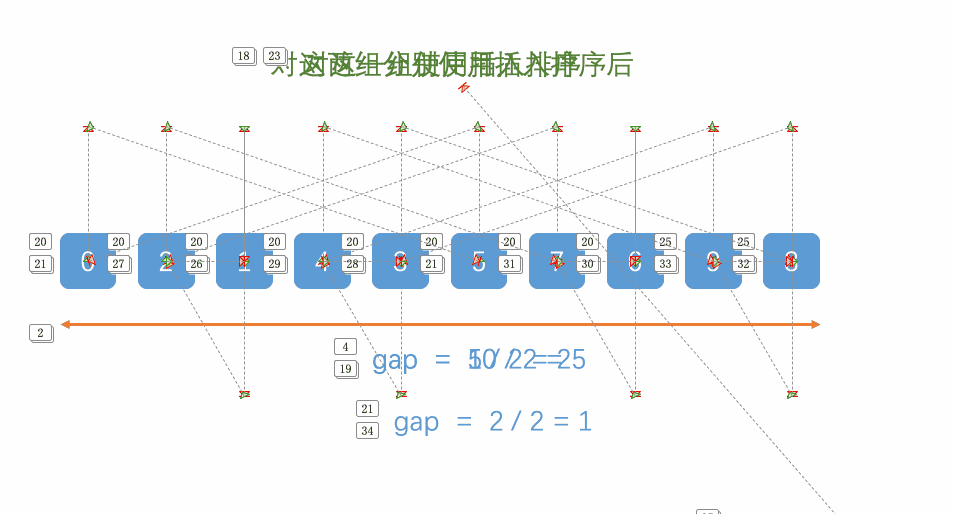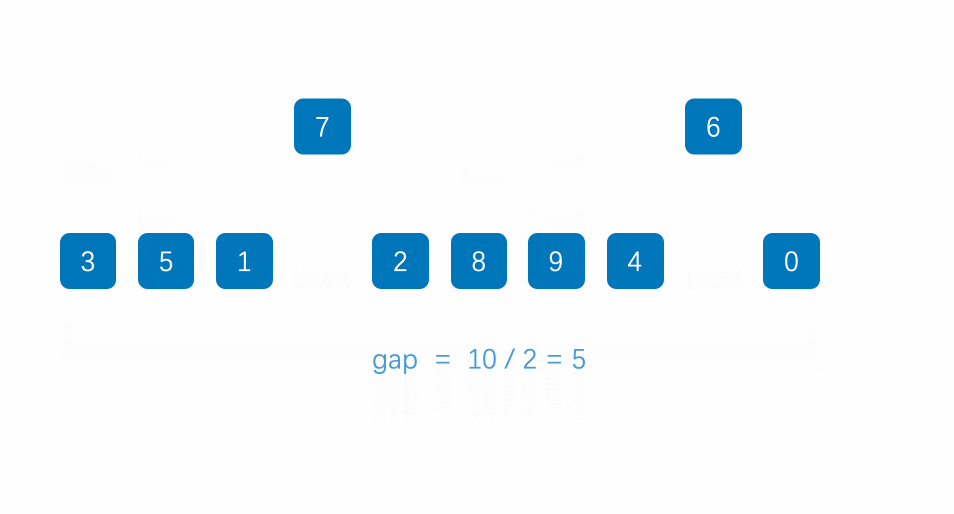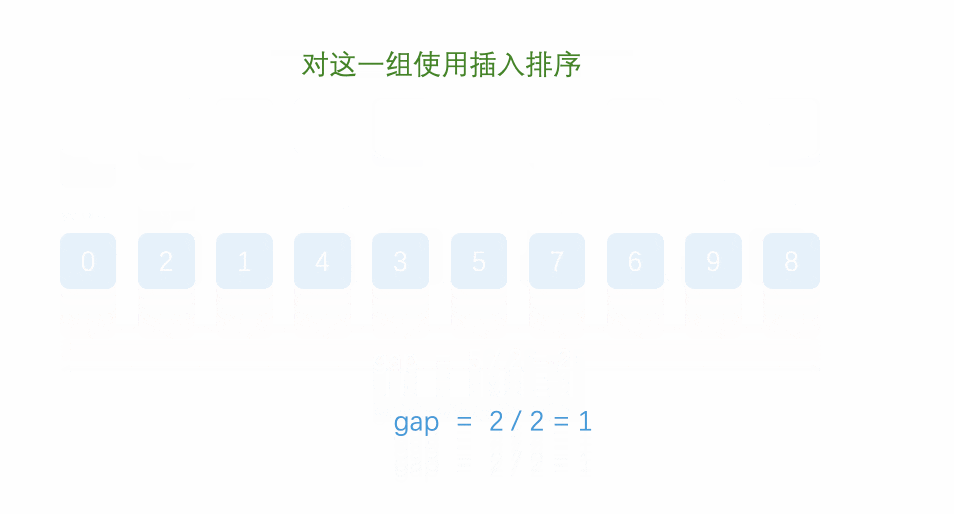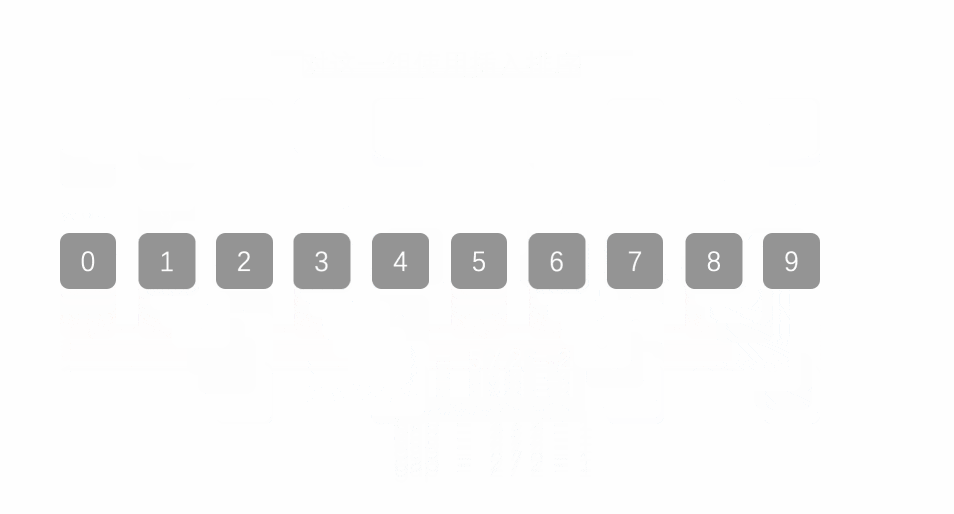
时间复杂度:(O(N^1.3))。
空间复杂度:(O(1))。
稳定性:不稳定。
代码实现
此处与图示取gap不同,取更为优化的循环gap = gap / 3 + 1,这样也能保证最后一次为1。
void ShellSort(int* a, int n)
{
int gap = n;
while(gap > 1)
{
// +1保证最后一个gap一定是1
// gap > 1时是预排序
// gap == 1时是插入排序
gap = gap / 3 + 1;
for(int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}5.堆排序
思路
堆排序是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
将数组通过向下调整算法建成一个堆,然后通过循环把堆顶元素与堆尾元素交换,再将堆用向下调整算法重新调整,重复调整成升序(降序)。
时间复杂度:(O(NlogN))。
空间复杂度:(O(1))。
稳定性:不稳定。
代码实现
//向下调整
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while(child < n)//找不到孩子
{
//找出小的孩子
if(child + 1 < n && a[child + 1] > a[child])
{
child = child + 1;
}
//调整
if(a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}//堆排序(O(N*logN))
void HeapSort(int* a, int n)
{
//降序,建小堆
//升序,建大堆
// for(int i = 1; i < n; i++)
// {
// AdjustUp(a, i);//向上调整建堆(O(N*logN))
// }
for(int i = (n-1-1)/2; i >= 0; i--)
{
AdjustDown(a, n, i);//向下调整建堆(O(N))
}
int end = n - 1;
//(O(N*logN))
while(end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}6.快速排序(快排)
时间复杂度:(O(NlogN)) 有序时退化成(O(N^2))。
空间复杂度:(O(logN))。(易错)
稳定性:不稳定。
快排里面的hoare法,双指针法以及一种非递归方法(还有三数取中,小区间优化两个优化策略)
可以看我这篇博文快速排序(Quick Sort)算法详解(递归与非递归)-CSDN博客
本文介绍两种快排优化:
一.三路划分
思路
三路划分问题主要来解决数组中存在大量重复数的问题,把所有重复数放在同一个区域可以大大提高效率,不过这样的代价也会牺牲一些其他无重复值时的效率。

这里的key可以使用随机数选key的策略以提高效率。
代码实现
/快速排序(递归) 三路划分 适用于多个相同值的情况
void QuickSort1(int* a, int left, int right)
{
if(left >= right)
return;
//小区间优化
if((right - left + 1) < 10)
{
InsertSort(a + left, right - left + 1);
}
else
{
随机数选key可以自行实现.
int key = a[left];
int cur = left + 1;
int begin = left;
int end = right;
while(cur <= end)
{
if(a[cur] < key)
{
Swap(&a[begin], &a[cur]);
begin++;
cur++;
}
else if(a[cur] > key)
{
Swap(&a[cur], &a[end]);
end--;
}
else
{
cur++;
}
}
QuickSort1(a, left , begin - 1);
QuickSort1(a, end + 1 , right);
}
}二.自省排序
思路
这是快排在数据库中的基本代码,拥有足够的优化策略。
这里基本快排代码依旧使用hoare法的找小与找大与小区间优化(具体思路可看上述文章)。
这里要讲的是防止选key时出现二叉树(递归)层数过深的情况下引起的效率降低。
此处定义一个logn用于记录最佳情况下选key的递归深度。当函数递归深度大于两倍logn时使用其他排序方案来提高排序效率,这里使用n*logn的堆排序。
代码实现
//自省排序
void IntroSort(int* a, int left, int right, int depth, int defaultDepth)
{
if(left >= right)
return;
if(right - left + 1 < 16)
{
InsertSort(a + left, right - left + 1);
return;
}
if(depth > defaultDepth)
{
HeapSort(a + left, right - left + 1);
return;
}
depth++;
//随机数取key
int tmp = left + (rand() % (right - left + 1));
Swap(&a[left], &a[tmp]);
int key = left;
int begin = left;
int end = right;
while(begin < end)
{
while(begin < end && a[end] > a[key])
{
end--;
}
while(begin < end && a[begin] <= a[key])
{
begin++;
}
Swap(&a[end], &a[begin]);
}
Swap(&a[key], &a[begin]);
key = begin;
IntroSort(a, left, key - 1, depth, defaultDepth);
IntroSort(a, key + 1, right, depth, defaultDepth);
}//快排升级版- 自省排序
void QuickSortPlus(int* a, int left, int right)
{
int depth = 0;
int logn = 0;
int n = right - left + 1;
for(int i = 1; i < n; i *= 2)
{
logn++;
}
// introspective sort -- ⾃省排序
IntroSort(a, left, right, depth, logn*2);
}7.归并排序
时间复杂度:(O(NlogN))。
空间复杂度:(O(N))。
稳定性:稳定。
1.递归法
思路
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
将一个数组先通过取中递归的方式拆分成1个单元,再通过归并来使各个分序列有序。如图示

代码实现
//归并子函数
void _MergeSort(int* a, int* tmp, int left, int right)
{
if(left >= right)
return;
int mid = (left + right) / 2;
_MergeSort(a, tmp, left, mid);
_MergeSort(a, tmp, mid + 1, right);
//归并
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int count = left;
while(begin1 <= end1 && begin2 <= end2)
{
if(a[begin1] <= a[begin2])
tmp[count++] = a[begin1++];
else
tmp[count++] = a[begin2++];
}
while(begin1 <= end1)
tmp[count++] = a[begin1++];
while(begin2 <= end2)
tmp[count++] = a[begin2++];
memcpy(a + left, tmp + left, (right - left + 1) * sizeof(int));
}//归并排序(递归)
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if(tmp == NULL)
{
perror("malloc fail!");
exit(1);
}
_MergeSort(a, tmp, 0, n - 1);
free(tmp);
tmp = NULL;
}
2.非递归法
思路
定义一个gap来定义每组归并数据的数据个数,gap每次取二的倍数,再通过归并来实现排序 如图:

可能你会发现:如果数据个数不是二的倍数,那是不是会存在越界访问的风险?
举十个数据为例如图:
可见后几位似乎都出现了越界,那么共会出现三种情况,可以把后两种归为一类,让最后一组数据不再归并,最后必然出现两组数归并的情况,并且最后一次归并begin2必然不越界,此时修正end2即可形成8.2归并,实现归并排序。
代码实现
//归并排序(非递归)
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if(tmp == NULL)
{
perror("malloc fail!");
exit(1);
}
//归并
int gap = 1;
while(gap < n)
{
for(int i = 0; i < n; i += gap * 2)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + gap * 2 - 1;
//两个修正的解释:举10个数为例依次进行11.22.44归并,最后两个数不纳入归并,
//最后一次归并begin2必然不越界,此时修正end2即可形成8.2归并,实现归并排序
//第二组都越界不存在,这一组就不需要归并
if(begin2 > n)
{
break;
}
//第二组的begin2没越界,end2越界,需要修正end2取值,重新归并
if(end2 > n)
{
end2 = n - 1;
}
int count = i;
while(begin1 <= end1 && begin2 <= end2)
{
if(a[begin1] <= a[begin2])
tmp[count++] = a[begin1++];
else
tmp[count++] = a[begin2++];
}
while(begin1 <= end1)
tmp[count++] = a[begin1++];
while(begin2 <= end2)
tmp[count++] = a[begin2++];
memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}8. 计数排序
思路
计数排序是一种非比较排序算法。它的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中 该被开辟的数组空间大小为原数组max - min + 1。以该数组下标为数值,原数组有这个数则a[i]++。
时间复杂度:(O(N + range))。(range为开辟的数组空间大小)
空间复杂度:(O(range))。
代码实现
//计数排序
// 时间复杂度:O(N+range)
// 只适合整数/适合范围集中
// 空间复杂度:O(range)
void CountSort(int* a, int n)
{
int min = 0, max = 0;
for(int i = 1; i < n; i++)
{
if(a[i] > a[max])
max = i;
if(a[i] < a[min])
min = i;
}
int range = a[max] - a[min] + 1;
int* count = (int*)calloc(range, sizeof(int));
if(count == NULL)
{
perror("calloc fail!");
exit(1);
}
for(int i = 0; i < n; i++)
{
count[a[i] - a[min]]++; // 计数
}
//排序
int j = 0;
for(int i = 0; i < range; i++)
{
while(count[i]--)
a[j++] = i + a[min];
}
free(count);
count = NULL;
}总结(附排序训练OJ题)
读完本文,你可以在该OJ题上进行实操来加深印象:912. 排序数组 - 力扣(LeetCode)
不同的排序算法有不同的时间复杂度和空间复杂度,适用于不同的场景。在实际应用中,我们需要根据数据的特点和需求选择合适的排序算法。例如,当数据量较小且基本有序时,插入排序可能是一个不错的选择;而当数据量较大时,快速排序、归并排序和堆排序通常表现更好。计数排序则适用于数据范围较小且为整数的情况。
通过本文的介绍和代码实现,相信你对八大排序算法有了更深入的理解。希望这些知识能帮助你在实际编程中更好地处理排序问题。