【算法题】算法一本通

每周更新至完结，建议关注收藏点赞。

待整理文章

CodeCreek
[题单]
算法专栏

已整理的文章

以前发布的算法题文章都会汇总在这里，重新整理复习，优化内容，并注明出处。
本文所选题目均含有原题地址。以JS为主，补充其他语言代码。
算法题第一弹
算法题第二弹
算法题第三弹

部分代码借鉴灵神

方法论

超过10分钟就要看题解
动态规划做100道才算入门
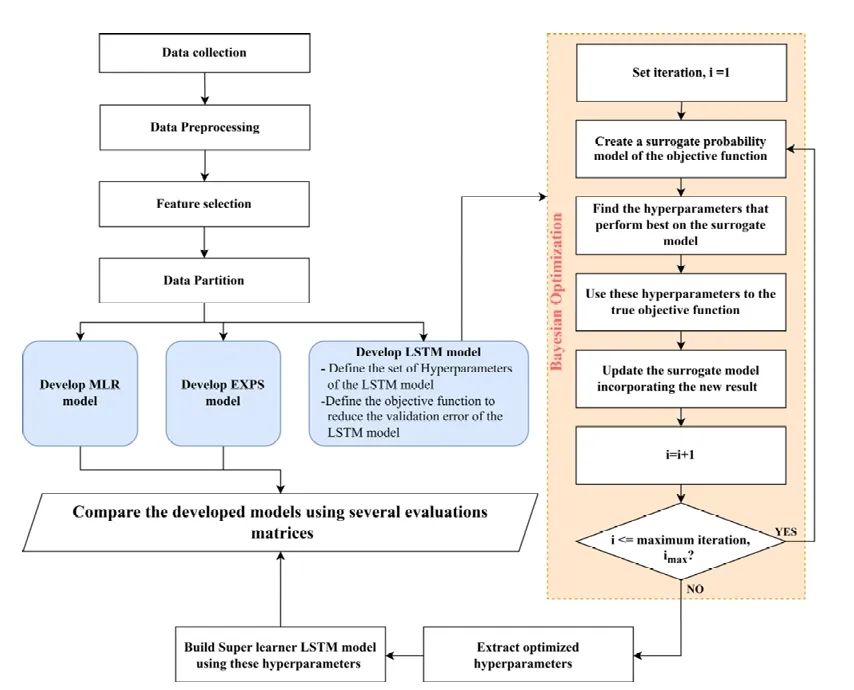
按照专题分类，每专题做完进行总结->按分类拓扑图顺序从前往后->定期复习。
在这里插入图片描述

由上面拓扑图可以得到顺序：

数组与哈希表
栈
双指针（滑动窗口、二分查找、链表）
树
前缀树
堆优先队列（区间/间隔问题、贪心）
回溯
图
一维DP
位操作
数学与几何学
二维DP
随缘更新：高级图论

思想总结

空间换时间

模版工具总结

哈希表：O(1) 快速找到元素
集合Set：O(n) 快速去重
KMP：O(m+n) 找子串（模式串）
核心思想就是根据子串的相同前后缀，标记“子串回退的下标”，便于回退。例如：字符串 aabaaab的前缀函数值依次为 0,1,0,1,2,2,3。

var strStr = function(haystack, needle) {//母串，子串
    const n = haystack.length, m = needle.length;
    if (m === 0) {
        return 0;
    }
    const pi = new Array(m).fill(0);//制作next数组
    //pi[0]必然是0，所以i从1开始
    for (let i = 1, j = 0; i < m; i++) {
        while (j > 0 && needle[i] !== needle[j]) {
            j = pi[j - 1];
        }
        if (needle[i] == needle[j]) {
            j++;
        }
        pi[i] = j;
    }
    //字符串匹配
    for (let i = 0, j = 0; i < n; i++) {
        while (j > 0 && haystack[i] != needle[j]) {
            j = pi[j - 1];
        }
        if (haystack[i] == needle[j]) {
            j++;
        }
        if (j === m) {
            return i - m + 1;
        }
    }
    return -1;
};

排序

堆排序
桶排序

数组与哈希表

两数之和
给定一个整数数组和一个目标值，找出数组中和为目标值的两个数的下标。
用哈希表记录值和下标，在遍历过程中判断[目标值减当前值]是否已存在
坑：先查再放，否则会匹配到自己

//js
var twoSum = function(nums, target) {
    const idx = new Map(); // 创建一个空哈希表
    for (let j = 0; ; j++) { // 枚举 j
        const x = nums[j];
        // 在左边找 nums[i]，满足 nums[i]+x=target
        if (idx.has(target - x)) { // 找到了
            return [idx.get(target - x), j]; // 返回两个数的下标
        }
        idx.set(x, j); // 保存 nums[j] 和 j
    }
};

存在重复元素

//js
var containsDuplicate = function(nums) {
    return new Set(nums).size < nums.length;
};

有效的字母异位词
用字符的ascii码作为下标，值为出现的次数，比对两个数组的值

//js
var isAnagram = function(s, t) {
    const cnt = Array(26).fill(0);
    for (const c of s) {
        cnt[c.charCodeAt(0) - 'a'.charCodeAt(0)]++;
    }
    for (const c of t) {
        cnt[c.charCodeAt(0) - 'a'.charCodeAt(0)]--;
    }
    return cnt.every(c => c === 0);
}

//by the way:
    return _.isEqual(cntS, cntT);//深比较
    //_代表库别名，最常见的是 Lodash 或 Underscore.js库函数。

字母异位词分组
字母异位词分组：就是把字母及数目相同，顺序不同的单词放到一组
用排序后的字符串作为 key 分组，哈希表记录分组
时间复杂度：O(n * k log k)

//js
var groupAnagrams = function(strs) {
    const m = new Map();
    for (const s of strs) {
        // 把 s 排序，作为哈希表的 key
        const sortedS = s.split('').sort().join('');
        if (!m.has(sortedS)) {
            m.set(sortedS, []);
        }
        // 排序后相同的字符串分到同一组
        m.get(sortedS).push(s);
    }
    // 哈希表的 value 保存分组后的结果
    return Array.from(m.values());
};

除自身以外数组的乘积
构建两个数组，前缀乘积pre、后缀乘积post，答案就等于它们相乘。
优化：要求O(1) 的额外空间复杂度，输出数组不被视为额外空间
先计算post，后计算pre，把pre直接乘到post中，最后返回post，相当于post直接作为answer
上述无论怎么优化，都至少需要两个先后的循环
前 K 个高频元素
两种方法，堆、桶排序。补充
JS可以直接通过Map+Array做出来

let topKFrequent = function(nums, k) {
    let map = new Map(), arr = [...new Set(nums)]
    nums.map((num) => {
        if(map.has(num)) map.set(num, map.get(num)+1)
        else map.set(num, 1)
    })
    return arr.sort((a, b) => map.get(b) - map.get(a)).slice(0, k);
};

有效的数独
最长连续序列
这个题目不能排序，因为要求O（n）时间复杂度

核心思路：
1）找起点：对于 nums 中的元素 x，如果有x-1，起点为x-1，以此类推，得到起点。
2）统计序列长度：每次找到起点y，不断查找下一个数 y+1,y+2,⋯ 是否在 nums 中，并更新序列长度。

var longestConsecutive = function(nums) {
    let ans = 0;
    const st = new Set(nums); // 把 nums 转成哈希集合
    for (const x of st) { // 遍历哈希集合
        if (st.has(x - 1)) {
            continue;
        }
        // x 是序列的起点
        let y = x + 1;
        while (st.has(y)) { // 不断查找下一个数是否在哈希集合中
            y++;
        }
        // 循环结束后，y-1 是最后一个在哈希集合中的数
        ans = Math.max(ans, y - x); // 从 x 到 y-1 一共 y-x 个数
    }
    return ans;
};

整数反转

//js
Number.parseInt('123-')//好处在于它不会理会后面的非法字符，返回123

var reverse = function(x) {    
	let re=x>=0 ? Number.parseInt(x.toString().split('').reverse().join('')) : Number.parseInt('-'+x.toString().split('').reverse().join(''))
	re=re<(-2)**31 || re>(2**31)-1 ? 0 : re    
	return re;
};

罗马整数
本题的难点在于处理六种特殊规则，但可以统一规则：
设 x=s[i−1], y=s[i]，这是两个相邻的罗马数字。
如果 x 的数值小于 y 的数值，那么 x 的数值要取相反数。例如 IV 中的 I 相当于 −1。
把所有数值相加，即为答案。

//js
const ROMAN = {
    'I': 1,
    'V': 5,
    'X': 10,
    'L': 50,
    'C': 100,
    'D': 500,
    'M': 1000,
};

var romanToInt = function(s) {
    let ans = 0;
    for (let i = 1; i < s.length; i++) { // 遍历相邻的罗马数字
        const x = ROMAN[s[i - 1]], y = ROMAN[s[i]];
        ans += x < y ? -x : x;
    }
    return ans + ROMAN[s[s.length - 1]]; // 加上最后一个
};

展开与压缩序列：报数序列是一个整数序列，按照其中的整数的顺序进行报数，得到下一个数。其前五项如下：
```
1
```
```
11
```
```
21
```
```
1211
```
```
111221
```

1 被读作 “one 1” (“一个一”) , 即 11。
11 被读作 “two 1s” (“两个一”）, 即 21。
21 被读作 “one 2”, “one 1” （“一个二” , “一个一”) , 即 1211。
给定一个正整数 n（1 ≤ n ≤ 30），输出报数序列的第 n 项。
注意：整数顺序将表示为一个字符串。
理解题意则很好写。规则：
1）有连续重复的则统计次数cnt++
2）无连续重复的，放入cnt，放入当前字符

var countAndSay = function(n) {
    let res=['','1','11','21','1211'];
    if(n<5)return res[n];
    for (let i=4;i<=n;i++){
        let str=res[i];
        let n=str.length;
        let res_temp='';
        let count=1;
        for(let j=0;j<n;j++){
            if(str[j]==str[j+1])count+=1;
            else{
                res_temp+=`${count}${str[j]}`;
                count=1;
            }
        }
        res.push(res_temp);
        //console.log(res);
    }
    return res[n];
};

栈

括号匹配

//最简洁代码
var isValid = function(s) {    
	let origin=s;    
	while(s.length){
		s=origin.replace('()','').replace('[]','').replace('{}',''); 
		if(s==origin)return false;        
		origin=s;    
	}    
	return true;
};

双指针（滑动窗口、二分查找、链表）

二分查找

var search = function(nums, target) {
    let left = 0, right = nums.length - 1;
    while (left <= right) {
        const mid = Math.floor((right + left) / 2);
        const num = nums[mid];
        if (num === target) {
            return mid;
        } else if (num > target) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return -1;
};

原地删除排序数组中的重复元素，返回移除后数组的新长度。
要求 O(1) 额外空间

var removeDuplicates = function(nums) {
    let i=0,j=1;
    while(j!=nums.length){
        if(nums[i]==nums[j])j+=1;
        else{
            i+=1;
            nums[i]=nums[j];
            j+=1
        }
    }
    return i+1;
};

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。假设数组中无重复元素。

var searchInsert = function(nums, target) {
    let i=0,j=nums.length-1;
    while(i<=j){
        let mid=(i+j)>>1;//位运算提高性能
        if(nums[mid]==target)return mid;
        else if(nums[mid]<target)i=mid+1;
        else j=mid-1;
    }
    return i;
};

合并两个有序链表
递归最简单

var mergeTwoLists = function(l1, l2) {    
	if (l1 === null) return l2;    
	else if (l2 === null) return l1;
	else if (l1.val < l2.val) {        
		l1.next = mergeTwoLists(l1.next, l2);        
		return l1;    
	} else {        
		l2.next = mergeTwoLists(l1, l2.next);        
		return l2;    
	}
};

树

前缀树

堆优先队列（区间/间隔问题、贪心）

回溯

数独游戏
玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个同色九宫内的数字均含1-9，不重复。
保证所有已知数据的格式都是合法的，并且题目有唯一的解。
格式要求，输入9行，每行9个字符，0代表未知，其它数字为已知。
输出9行，每行9个数字表示数独的解。例如：

#include <stdio.h>
int a[9][9];
 
int place(int x, int y) //二者分别是数组对应的行地址和列地址，取值为0-8
{
	int up, down, left, right;
	int i,j;
 
	up=x/3*3; //计算同色格子的范围
	down=up+3;
	left=y/3*3;
	right=left+3;
 
	//以下分三种情况判断是否在x,y对应的位置放这个数，如果不可以放，返回0，如果可以放，返回1，会进一步迭代
	
	for(i=0;i<9;i++){
		if(a[x][y]==a[i][y] && i!=x && a[i][y]!=0)
			return 0;		
	}
 
	for(i=0;i<9;i++){
		if (a[x][y]==a[x][i] && i!=y && a[x][i]!=0)
			return 0;		
	}
 
	for(i=up;i<down;i++)//同色9宫格的情况
	{
		for(j=left;j<right;j++)
			if(i!=x || j!=y)//不是自己即可
			{
				if(a[i][j]==a[x][y] && a[i][j]!=0)
					return 0;
			}
	}
 
	return 1;	
}
 
void backtrack(int t)//第几个格子
{
	int i,j;
	int x,y;
 
	if(t==81)
	{
		for(i=0;i<9;i++)
		{
			for(j=0;j<9;j++)
				printf("%d",a[i][j]);		
			putchar('\n');
		}
	}
	else
	{
		x=t/9;
		y=t%9; //将这个转换为相应的数组行坐标和列坐标
		if(a[x][y]!=0)backtrack(t+1);
		else
		{
			for(i=1;i<10;i++)
			{
				a[x][y]=i;
				if(place(x,y)==1)
					backtrack(t+1);
				a[x][y]=0;//回溯操作
			}
		}
	}
}
 
int main()
{
	char str[9][9];
	int i,j;
 
	for(i=0;i<9;i++)
		gets(str[i]);
 
	for(i=0;i<9;i++)
		for(j=0;j<9;j++)
			a[i][j]=str[i][j]-'0';
	
	backtrack(0);
	return 0;
}

今有7对数字：两个1，两个2，两个3，…两个7，把它们排成一行。
要求，两个1间有1个其它数字，两个2间有2个其它数字，以此类推，两个7之间有7个其它数字。
如下就是一个符合要求的排列：17126425374635当然，如果把它倒过来，也是符合要求的。
请你找出另一种符合要求的排列法，并且这个排列法是以74开头的。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<stdlib.h>
#include<algorithm>
#include<cmath>
using namespace std;
int arr[16]={0};
int dfs(int n)
{
    if(n > 6) return 1;//因为7已经确定，所以最大放入数就是6
    if(n == 4) n++;//4的位置已经确定，所以跳过
    int i = 0;
    for(i = 3;i <=14 ;i++)
    {
        if(i == 7 || i == 9) continue;//7,9位置值已经定了
        if(i+n+1 <=14 && arr[i]==0 &&arr[i+n+1]==0)//保证两个位置都没有数据
        {
            arr[i] = arr[i+n+1] = n;
            if(dfs(n+1))//改变数字
                return 1;
            arr[i] = arr[i+n+1] = 0;//回溯回来证明不符合条件，恢复上一次dfs状态
        }
    }
    return 0;
}
int main()
{
    arr[1] = 7,arr[2] = 4;//因为题目上已经给出两个开头，可以推出后面两个
    arr[9] = 7,arr[7] = 4;
    dfs(1);//放入数字1
    for(int i = 1;i < 16;i++ )
    {
        cout <<arr[i];
    }
    cout <<"\n";
    return 0;
}

图

一维DP

位操作

整数反转

/**
 * @param {number} x
 * @return {number}
 */
var reverse = function(x) {
    let result = 0;
    while(x !== 0) {
        result = result * 10 + x % 10;
        x = (x / 10) | 0;
        //通过 | 0 取整，无论正负，只移除小数点部分（正数向下取整，负数向上取整）。
    }
    return (result | 0) === result ? result : 0;
    //|只能处理32位内的，所以可以用来判断是否溢出32位
};

为啥通过 | 0 取整，无论正负，只移除小数点部分（正数向下取整，负数向上取整）？
在 JavaScript 中，当你对一个数字执行位运算符（如 |、&、^、~、<<、>>、>>>）时，JavaScript 引擎会执行以下步骤：
将操作数转换为 32 位带符号整数。（故局限性也是只能处理32位带符号整数范围内）
当一个浮点数被转换为 32 位整数时，它的小数部分会被直接截断（丢弃）。
x | 0得到x本身，所以说这个操作只是去除小数部分。

数学与几何学

x的x次幂结果为10，计算出x的近似值，这个值是介于2和3之间的一个数字。x的值计算到小数后6位（四舍五入）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<stdlib.h>
#include<algorithm>
#include<cmath>
using namespace std;

int main()
{
	double a=2.0;
	for(;a<3;a+=0.0000001)//要比要求的6位小数多出一位才能四舍五入
	{
		if(fabs(pow(a,a)-10.0)<0.000001)
		break;
	}
	printf("%6lf",a); //lf是double格式 
    return 0;
}

大数勾股定理
已知直角三角形的斜边是某个整数，并且要求另外两条边也必须是整数。求满足这个条件的不同直角三角形的个数。
输入一个整数 n (0<n<10000000) 表示直角三角形斜边的长度。要求输出一个整数，表示满足条件的直角三角形个数。
资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms

#include<stdio.h>
#include<math.h>
int main()
{
    long long n,i,j,sum=0,m;
    //~按位取反
    //使得当 scanf 读取失败时 返回EOF (-1)
    //-1 是 32 位整数 1...1111 (所有位都是 1) 则循环终止
    while(~scanf("%lld",&n))
    {
        for(i=1;i<n;i++)
        {
            j=sqrt(n*n-i*i);
            if(j*j==n*n-i*i)
            sum++;
        }
        printf("%lld\n",sum/2);
    }
    return 0;
 }

埃及分数
形如：1/a 的分数称为单位分数。可以把1分解为若干个互不相同的单位分数之和。
例如：
1 = 1/2 + 1/3 + 1/9 + 1/18
1 = 1/2 + 1/3 + 1/10 + 1/15
1 = 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/15 + 1/35 + 1/45 + 1/231
等等，类似这样的分解无穷无尽。
我们增加一个约束条件：最大的分母必须不超过30
请你求出分解为n项时的所有不同分解法。
数据格式要求：
输入一个整数n，表示要分解为n项（n<12）
输出分解后的单位分数项，中间用一个空格分开。
每种分解法占用一行，行间的顺序按照分母从小到大排序。
例如，
输入：
4
程序应该输出：
1/2 1/3 1/8 1/24
1/2 1/3 1/9 1/18
1/2 1/3 1/10 1/15
1/2 1/4 1/5 1/20
1/2 1/4 1/6 1/12
再例如，
输入：
5
程序应该输出：
1/2 1/3 1/12 1/21 1/28
1/2 1/4 1/6 1/21 1/28
1/2 1/4 1/7 1/14 1/28
1/2 1/4 1/8 1/12 1/24
1/2 1/4 1/9 1/12 1/18
1/2 1/4 1/10 1/12 1/15
1/2 1/5 1/6 1/12 1/20
1/3 1/4 1/5 1/6 1/20
资源约定：
峰值内存消耗 < 256M
CPU消耗 < 2000ms

先研究一下数学原理 1=30/30
这个分母就是30，分子也是30，将分子的30做分解就可以了。列出1-29之内相加等于30的各种可能，然后将这些数和分母约分就可以了
比如:30=2+3+25
则1=(2+3+25)/30
1=1/15+1/10+5/6
加了限制项n 时，就更加好办了，就是求n个数相加等于30
等式可以认为是(a1+a2+…am)/K，很好理解，a1,…am必然是K的所有约数的和的组合。因此最后题目就是转化为求一个数K的所有约数（质因子），题目K最大才30，之后求出所有约数中,n个数的和等于K的组合。
比如：K=30，30=235，根据“约数个数定理”，约数有8个，除去自己本身和1就剩6个，为2,3,5,6,10,15,
如果你输入n=4，那么就是求这6个约数中，哪4个相加正好等于30的所有组合，根据组合原理，C(7,4)才210中组合，因此循环不会很久。
题目没规定K值，因此，需要K从1到30循环，对每一次循环的K，找出所有所有约数，并对所有约数个数不小于n的情况，循环找出所有n个约数等于K的组合。
建议搜索：
1、约数个数定理
2、求求一个数的所有约数（或者质因子）
3、从N个数中任选M个数相加的和等于K（循环应该就能解决）