一 Bresenham 绘直线

    使用 Bresenham 算法，可以在显示器上绘制一直线段。该算法主要思想如下：

    1 给出直线段上两个端点 

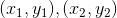
，根据端点求出直线在X,Y方向上变化速率 

；

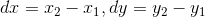
    2 当 

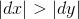
 时，X 方向上变化速率快于 Y 方向上变化速率，选择在 X 方向上迭代，在每次迭代中计算 Y 轴上变化；

       当 

 时，Y 方向上变化速率快于 X 方向上变化速率，选择在 Y 方向上迭代，在每次迭代中计算 X 轴上变化；

    3 现在仅考虑 

 情形，在 

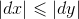
 情况下仅需要交换变量即可。直线斜率 

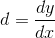
，当 d = 0 时，为一条水平直线，当 d > 0 或 d < 0 时，需要分开讨论，如下图：

        

二 Bresenham 绘圆

    使用 Bresenham 绘制圆形，只需要绘制四分之一圆即可，其他部分通过翻转图形即可得到。假设圆心位于 (0, 0) 点，半径为  R，绘制第一象限四分之一圆形，如下图：

      

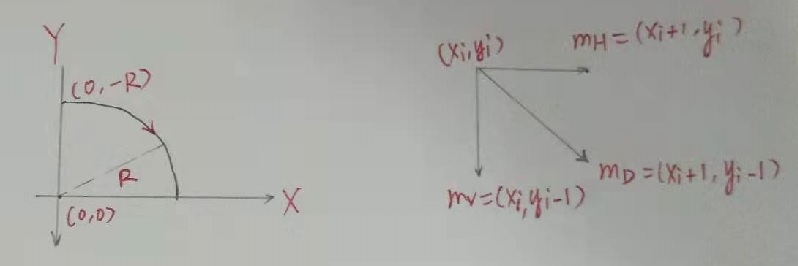
    根据图形可知，从 

 出发，下一个可能的选择分别为：

    1）水平方向上  

；

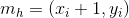
    2）对角方向上 

；

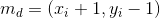
    3）垂直方向上 

；

    下面计算

，根据差值可判断大致圆弧位置：

    1）当 

 时，圆环落在 

 与 

 之间，进一步计算圆弧到 

 与 

 的距离以判断应该落在哪个点上；

    2）

，

         由于 

，

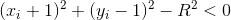
，上式可化简为，

         

，将 

 改写为 

 得：

         

，

        已知 

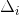
，可根据上式快速求解出 

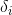
，当 

时，下一点落在 

 上，当 

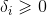
 时，下一点落在 

 上；

    3）当 

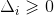
 时，圆环落在 

 与 

 之间，进一步计算圆弧到 

 和 

 的距离以判断应该落在哪个点上；

    4）

，可化简为：

         

，将 

 改写为 

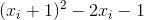
 得：

        

，

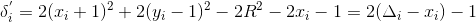
       已知 

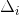
，可根据上式快速求解出 

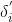
，当 

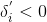
 时，下一点落在 

 上，当 

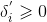
 时，下一点落在 

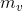
 上；

    5）以上推导中，已知 

 可以快速求解 

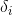
，同时，已知 

 也可以快速推导出 

，以下分类讨论：

         a. 当 

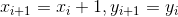
时，有：

             

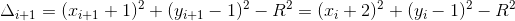
，进一步整理得：

            

；

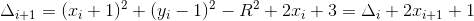
        b. 当 

 时，有：

            

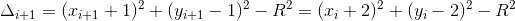
，进一步整理得：

           

；

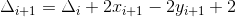
       c. 当 

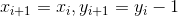
 时，有：

           

，进一步整理得：

           

。

    以下给出 Bresenham 绘圆实现：

      

 1     void Bresenham_Circle(PairS center, int radius, std::vector<PairS>& circle)
 2     {
 3         PairS start(0, radius);
 4         int Delta = (start.x + 1) * (start.x + 1) +
 5             (start.y - 1) * (start.y - 1) - radius * radius;
 6 
 7         std::vector<PairS> tmp;
 8         tmp.push_back(start);
 9 
10         while (start.y > 0)
11         {
12             int state = -1;
13 
14             if (Delta < 0)
15             {
16                 int delta = (Delta + start.y) * 2 - 1;
17                 if (delta < 0)
18                 {
19                     start.x += 1;
20                     state = 0;
21                 }
22                 else
23                 {
24                     start.x += 1;
25                     start.y -= 1;
26                     state = 1;
27                 }
28             }
29             else
30             {
31                 int delta = (Delta - start.x) * 2 - 1;
32                 if (delta < 0)
33                 {
34                     start.x += 1;
35                     start.y -= 1;
36                     state = 1;
37                 }
38                 else
39                 {
40                     start.y -= 1;
41                     state = 2;
42                 }
43             }
44 
45             if (state == 0)
46                 Delta = Delta + start.x * 2 + 1;
47             else if (state == 1)
48                 Delta = Delta + start.x * 2 - start.y * 2, +2;
49             else if (state == 2)
50                 Delta = Delta - start.y * 2 + 1;
51             else
52                 break;
53 
54             tmp.push_back(start);
55         }
56 
57         std::vector<PairS> tmp2;
58         for (int i = 0; i < tmp.size(); ++i)
59         {
60             PairS p(tmp[i].x, tmp[i].y);
61             tmp2.push_back(p);
62         }
63         for (int i = tmp.size() - 1; i >= 0; --i)
64         {
65             PairS p(tmp[i].x, -tmp[i].y);
66             tmp2.push_back(p);
67         }
68         for (int i = 0; i < tmp2.size(); ++i)
69         {
70             PairS p(tmp2[i].x, tmp2[i].y);
71             circle.push_back(p);
72         }
73 
74         for (int i = tmp2.size() - 1; i >= 0; --i)
75         {
76             PairS p(-tmp2[i].x, tmp2[i].y);
77             circle.push_back(p);
78         }
79 
80         for (int i = 0; i < circle.size(); ++i)
81         {
82             circle[i].x += center.x;
83             circle[i].y += center.y;
84         }
85     }