[蓝桥杯]生物芯片

news2025/6/6 12:17:41

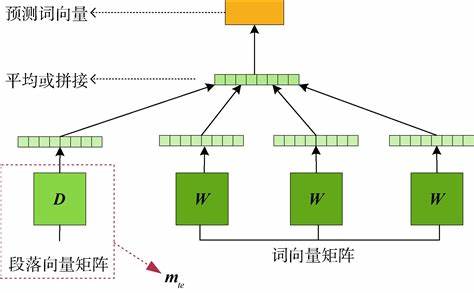
生物芯片

题目描述

X 博士正在研究一种生物芯片，其逻辑密集度、容量都远远高于普通的半导体芯片。

博士在芯片中设计了 nn 个微型光源，每个光源操作一次就会改变其状态，即：点亮转为关闭，或关闭转为点亮。

这些光源的编号从 1 到 nn，开始的时候所有光源都是关闭的。

博士计划在芯片上执行如下动作：

所有编号为 2 的倍数的光源操作一次，也就是把 2 4 6 8 ⋯⋯ 等序号光源打开;

所有编号为 3 的倍数的光源操作一次, 也就是对 3 6 9 ⋯⋯ 等序号光源操作，注意此时 6 号光源又关闭了。

所有编号为 4 的倍数的光源操作一次。

⋯⋯

直到编号为 nn 的倍数的光源操作一次。

X 博士想知道：经过这些操作后，某个区间中的哪些光源是点亮的。

输入描述

输入 3 个用空格分开的整数：N L R(L<R<N<1015)N L R(L<R<N<1015)，NN 表示光源数，LL 表示区间的左边界，RR 表示区间的右边界。

输出描述

输出 1 个整数，表示经过所有操作后，[L,R][L,R] 区间中有多少个光源是点亮的。

输入输出样例

示例

输入

5 2 3

输出

运行限制

最大运行时间：1s
最大运行内存: 256M

总通过次数: 382 | 总提交次数: 550 | 通过率: 69.5%

难度: 中等标签: 2014, 思维, 国赛

问题分析

操作规则：
- 初始状态：所有光源关闭。
- 执行操作：对编号为 k 的倍数光源切换状态（k 从 2 到 N）。
- 最终状态：操作奇数次的光源点亮，偶数次的光源关闭。
关键数学性质：
- 光源 x 被操作的次数等于其 除 1 以外的因子个数（因为操作从 k=2 开始）。
- 操作次数的奇偶性由因子个数决定：
  - 若 因子个数为奇数 → 操作次数为偶数 → 光源关闭。
  - 若 因子个数为偶数 → 操作次数为奇数 → 光源点亮。
- 完全平方数的因子个数为奇数（如 4 的因子是 1,2,4），因此最终关闭；非完全平方数的因子个数为偶数（如 2 的因子是 1,2），因此最终点亮。
问题转化：
- 求 [L, R] 中点亮的灯数 = 区间内 非完全平方数的个数。
- 公式：ans=(R−L+1)−(⌊R⌋−⌊L−1⌋)其中：
  - R−L+1：区间总光源数。
  - ⌊R⌋：≤ R 的最大完全平方数数量。
  - ⌊L−1⌋：< L 的最大完全平方数数量。
  - ```
  #include <iostream>
  #include <cmath>
  using namespace std;
  
  int main() {
      long long n, l, r;
      cin >> n >> l >> r;
  
      // 计算区间长度
      long long len = r - l + 1;
  
      // 计算 [1, L-1] 和 [1, R] 内的完全平方数数量
      long long a = (l - 1 > 0) ? (long long)sqrtl(l - 1) : 0;
      long long b = (long long)sqrtl(r);
  
      // 完全平方数在 [L, R] 中的数量
      long long count_square = b - a;
  
      // 非完全平方数数量 = 总光源数 - 完全平方数数量
      long long ans = len - count_square;
      cout << ans << endl;
  
      return 0;
  }
```
  代码解释
- 输入处理：
  - 读入 N（光源总数）、L（区间左边界）、R（区间右边界）。
- 区间长度计算：
  - len = r - l + 1 表示 [L, R] 内的总光源数。
- 完全平方数计数：
  - a = sqrtl(l-1)：计算 < L 的最大完全平方数数量（如 L=3 时，a = sqrt(2)≈1，对应完全平方数 1）。
  - b = sqrtl(r)：计算 ≤ R 的最大完全平方数数量（如 R=6 时，b = sqrt(6)≈2，对应完全平方数 1,4）。
  - count_square = b - a：区间 [L, R] 内完全平方数的数量（如 [3,6] 中只有 4）。
- 结果计算：
  - ans = len - count_square：非完全平方数数量即为点亮的灯数。
- 复杂度分析
- 时间复杂度：O(1)，仅需两次开方运算。
- 空间复杂度：O(1)，仅用常数级变量。
- 示例验证
- 输入 5 2 3：
  - 区间 [2,3] 总长度 = 2。
  - 完全平方数：无（a = sqrt(1)=1, b = sqrt(3)≈1 → count_square=0）。
  - 输出 2（正确）。
- 输入 10 3 6：
  - 区间 [3,6] 总长度 = 4。
  - 完全平方数：4（a = sqrt(2)≈1, b = sqrt(6)≈2 → count_square=1）。
  - 输出 3（正确）。